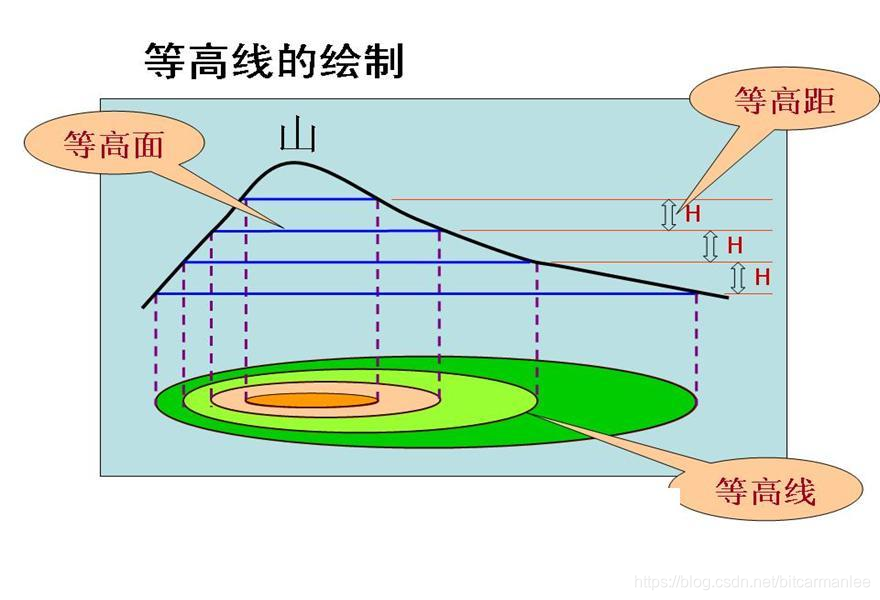
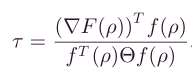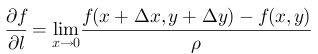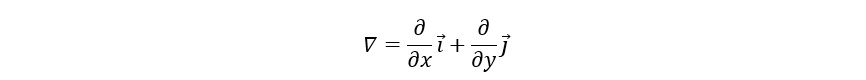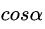很多时候,我们时间有限,对一些知识只能不求甚解,但这这些不求甚解的知识又会很困扰我们,总想着原理是啥,为啥这样做。就比如我们学梯度下降时,都知道梯度下降是机器学习、深度学习的核心优化算法,但为什么沿梯度方向,函数变化最快呢???
问了不少人都不能说的很清楚,所以查阅了很多博客,视频,现分享给大家。
导数
导数的几何意义可能很多人都比较熟悉: 当函数定义域和取值都在实数域中的时候,导数可以表示函数曲线上的切线斜率。 除了切线的斜率,导数还表示函数在该点的变化率。
比如中学学到的加速度 a = Δ v Δ t a=\frac{\Delta v}{\Delta t} a=ΔtΔv,这表示的是速度v对时间t的导数,物理意义表示的是速度变化的快慢。
放到数学上也是一样, 除了切线的斜率,导数还表示函数在该点的变化率也就是变化快慢。
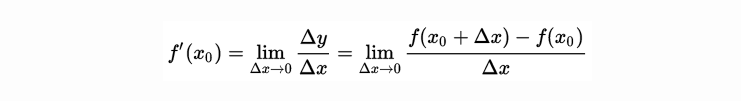
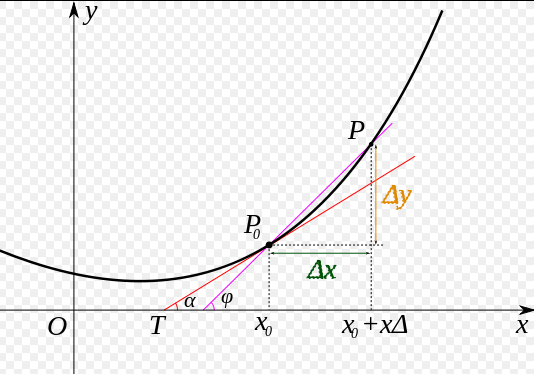
在一元函数中,只有一个自变量变动,也就是说只存在一个方向的变化率,也就没有沿哪个方向变化快慢的问题了。下面延伸到多元函数,以二元函数为例。
偏导数
沿x方向的方向导数:
l i m Δ x → 0 f ( x 0 + Δ x , y 0 ) − f ( x 0 , y 0 ) Δ x = ∂ z ∂ x (1) lim_{\Delta x\rightarrow0}\frac{f(x_0+\Delta x,y_0)-f(x_0,y_0)}{\Delta x}=\frac{\partial z}{\partial x}\tag{1} limΔx→0Δxf(x0+Δx,y0)−f(x0,y0)=∂x∂z(1)
移动下位置:
l i m Δ x → 0 f ( x 0 + Δ x , y 0 ) − f ( x 0 , y 0 ) = ∂ z ∂ x Δ x (2) lim_{\Delta x\rightarrow0}{f(x_0+\Delta x,y_0)-f(x_0,y_0)} =\frac{\partial z}{\partial x}{\Delta x}\tag{2} limΔx→0f(x0+Δx,y0)−f(x0,y0)=∂x∂zΔx(2)
沿y方向的方向导数:
l i m Δ y → 0 f ( x 0 , y 0 + Δ y ) − f ( x 0 , y 0 ) Δ y = ∂ z ∂ y (3) lim_{\Delta y\rightarrow0}\frac{f(x_0,y_0+\Delta y)-f(x_0,y_0)}{\Delta y}=\frac{\partial z}{\partial y}\tag{3} limΔy→0Δyf(x0,y0+Δy)−f(x0,y0)=∂y∂z(3)
移动下位置:
l i m Δ y → 0 f ( x 0 , y 0 + Δ y ) − f ( x 0 , y 0 ) = ∂ z ∂ y Δ y (4) lim_{\Delta y\rightarrow0}{f(x_0,y_0+\Delta y)-f(x_0,y_0)} =\frac{\partial z}{\partial y}{\Delta y} \tag{4} limΔy→0f(x0,y0+Δy)−f(x0,y0)=∂y∂zΔy(4)
2+4:
l i m Δ y → 0 l i m Δ x → 0 f ( x 0 + Δ x , y 0 + Δ y ) − f ( x 0 , y 0 ) = ∂ z ∂ y Δ y + ∂ z ∂ x Δ x (5) lim_{\Delta y\rightarrow0}lim_{\Delta x\rightarrow0}{f(x_0+\Delta x,y_0+\Delta y)-f(x_0,y_0)} =\frac{\partial z}{\partial y}{\Delta y} +\frac{\partial z}{\partial x}{\Delta x}\tag{5} limΔy→0limΔx→0f(x0+Δx,y0+Δy)−f(x0,y0)=∂y∂zΔy+∂x∂zΔx(5)
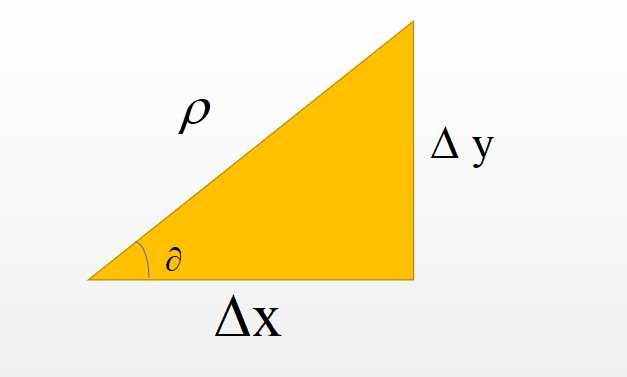
同时除 ρ \rho ρ
l i m Δ y → 0 l i m Δ x → 0 f ( x 0 + Δ x , y 0 + Δ y ) − f ( x 0 , y 0 ) ρ = ∂ z ∂ y Δ x ρ + ∂ z ∂ x Δ y ρ (6) lim_{\Delta y\rightarrow0}lim_{\Delta x\rightarrow0}\frac{{f(x_0+\Delta x,y_0+\Delta y)-f(x_0,y_0)}}{\rho} =\frac{\partial z}{\partial y}\frac{\Delta x}{\rho} +\frac{\partial z}{\partial x}\frac{\Delta y}{\rho}\tag{6} limΔy→0limΔx→0ρf(x0+Δx,y0+Δy)−f(x0,y0)=∂y∂zρΔx+∂x∂zρΔy(6)
l i m Δ y → 0 l i m Δ x → 0 f ( x 0 + Δ x , y 0 + Δ y ) − f ( x 0 , y 0 ) ρ = ∂ z ∂ y cos α + ∂ z ∂ x sin α (7) lim_{\Delta y\rightarrow0}lim_{\Delta x\rightarrow0}\frac{{f(x_0+\Delta x,y_0+\Delta y)-f(x_0,y_0)}}{\rho} =\frac{\partial z}{\partial y}\cos{\alpha} +\frac{\partial z}{\partial x}\sin{\alpha}\tag{7} limΔy→0limΔx→0ρf(x0+Δx,y0+Δy)−f(x0,y0)=∂y∂zcosα+∂x∂zsinα(7)
其中G为梯度,也就是沿x,y方向的导数组成的向量:
G = ( ∂ z ∂ y , ∂ z ∂ x ) G=(\frac{\partial z}{\partial y} ,\frac{\partial z}{\partial x}) G=(∂y∂z,∂x∂z)
I为方向导数的方向,这是一个单位向量
I = ( cos α , sin α ) I=(\cos{\alpha} ,\sin{\alpha}) I=(cosα,sinα)
方向导数:
方 向 导 数 = G ⋅ I = ∂ z ∂ y cos α + ∂ z ∂ x sin α = ∣ ∂ z ∂ y ∣ ∣ ∂ z ∂ x ∣ cos θ 方向导数=G\cdot{I} =\frac{\partial z}{\partial y}\cos{\alpha} +\frac{\partial z}{\partial x}\sin{\alpha}= |\frac{\partial z}{\partial y} ||\frac{\partial z}{\partial x}| \cos{\theta} 方向导数=G⋅I=∂y∂zcosα+∂x∂zsinα=∣∂y∂z∣∣∂x∂z∣cosθ
θ \theta θ为方向夹角
方向导数越大,表明函数上升越快,要想方向导数最大,即 cos θ \cos{\theta} cosθ要最大, cos θ ∈ ( − 1 , 1 ) \cos{\theta}\in {(-1,1)} cosθ∈(−1,1) 也就是 θ = 0 \theta=0 θ=0时,方向导数最大,上升最快; θ = π \theta=\pi θ=π时,方向导数为反方向最大,下降最快。
ok,以上证明完毕。