文章目录
- 前言
- 方向导数
- 梯度
- 方向导数公式的证明
前言
- 前文介绍了多元函数微分的实质,接下来介绍多元函数中的方向导数与梯度,以二元函数为例
方向导数
- 方向导数的实质:自变量沿着xoy平面上的某个方向变化时,f的变化率(一元函数微分)

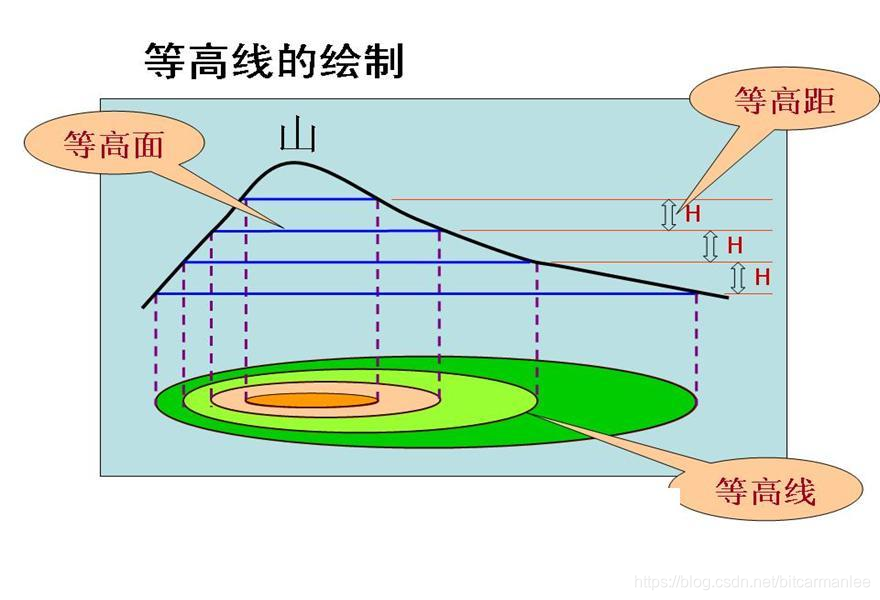
- 曲面S沿着u = (a, b)方向在(x0, y0, z0)的方向导数,是 作一平面C,C垂直于平面xoy且经过方向向量u所在的直线。C与S的交线(曲线)在(x0, y0, z0)的导数(一元函数微分)
- 请注意,此处沿着u方向,向量u是xoy平面上的单位向量,用于指示自变量的变化方向,而不是三维空间中的向量。由于u是单位向量,故必然存在 θ \theta θ,使得
c o s θ = a , s i n θ = b cos\theta = a, sin\theta = b cosθ=a,sinθ=b
- 易知, θ \theta θ就是向量u和x轴的夹角
- 例如我们熟知的两个偏导数,分别是沿着x轴和y轴的方向导数,即上图中的平面C应当垂直于xoy平面,且经过x轴(y轴)
- 根据上一篇文章对一元函数微分的讨论可知,该方向导数应当是(一元函数微分)
D u f ∣ ( x 0 , y 0 , z o ) = l i m h − > 0 f ( x 0 + h a , y 0 + h b ) − f ( x 0 , y 0 ) h ( ∗ ) D_u f |_{(x0, y0, zo)} = lim_{h->0} \frac{f(x_0 + ha, y_0 + hb) - f(x_0, y_0)}{h}\ \ (*) Duf∣(x0,y0,zo)=limh−>0hf(x0+ha,y0+hb)−f(x0,y0) (∗)
- 可以证明(见文末)
D u f ∣ ( x 0 , y 0 , z o ) = f x ( x 0 , y 0 ) a + f y ( x 0 , y 0 ) b D_u f |_{(x0, y0, zo)} = f_x(x_0, y_0)a + f_y(x_0, y_0)b Duf∣(x0,y0,zo)=fx(x0,y0)a+fy(x0,y0)b
= ( f x ( x 0 , y 0 ) , f y ( x 0 , y 0 ) ) ⋅ ( a , b ) = ∇ f ( x 0 , y 0 ) ⋅ u = (f_x(x_0, y_0), f_y(x_0, y_0)) · (a, b) = \nabla f(x_0, y_0) · u =(fx(x0,y0),fy(x0,y0))⋅(a,b)=∇f(x0,y0)⋅u
- ∇ f \nabla f ∇f是梯度,将在下文介绍
- 这里有几个重要的前提条件,*式成立的前提条件是给定的方向向量u是单位向量。根据上文可以进行如下转换,假设 θ \theta θ是沿着u方向的任意向量u’与x轴的夹角,则
D u ′ f ∣ ( x 0 , y 0 , z o ) = ∇ f ( x 0 , y 0 ) ⋅ ( c o s θ , s i n θ ) D_{u'} f |_{(x0, y0, zo)} = \nabla f(x_0, y_0) · (cos\theta, sin\theta) Du′f∣(x0,y0,zo)=∇f(x0,y0)⋅(cosθ,sinθ)
- 需要注意的是,方向导数是数,因为点乘的结果是实数,但下文可以看到,梯度是个自变量域的向量
梯度
- 定义梯度为向量 ∇ f = ( f x , f y ) \nabla f = (f_x, f_y) ∇f=(fx,fy)
- 在(x0, y0, z0)的梯度的实质是使得z0变化最快(即方向导数的绝对值最大)的自变量的变化方向的方向向量(不一定是单位向量)。梯度用于表明沿着哪个自变量的变化方向函数值变化最快
- 易知,假设u是任一单位方向向量, θ ′ \theta' θ′是向量 ∇ f = ( f x , f y ) \nabla f = (f_x, f_y) ∇f=(fx,fy)与 u = ( c o s θ , s i n θ ) u = (cos\theta, sin\theta) u=(cosθ,sinθ)的夹角
D u f ( x 0 , y 0 ) = ∇ f ( x 0 , y 0 ) ⋅ ( c o s θ , s i n θ ) = ∣ ∇ f ( x 0 , y 0 ) ∣ ∣ ( c o s θ , s i n θ ) ∣ c o s θ ′ D_u f(x_0, y_0) = \nabla f(x_0, y_0) · (cos\theta, sin\theta) = |\nabla f(x_0, y_0) ||(cos\theta, sin\theta) |cos\theta' Duf(x0,y0)=∇f(x0,y0)⋅(cosθ,sinθ)=∣∇f(x0,y0)∣∣(cosθ,sinθ)∣cosθ′
= ∣ ∇ f ( x 0 , y 0 ) ∣ c o s θ ′ = |\nabla f(x_0, y_0)|cos\theta' =∣∇f(x0,y0)∣cosθ′
- 显然,当且仅当两个向量同向时,即自变量的变化方向为梯度向量的方向,方向导数最大,f增长最快,增长率为梯度的模长;反向同理
方向导数公式的证明



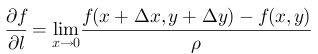



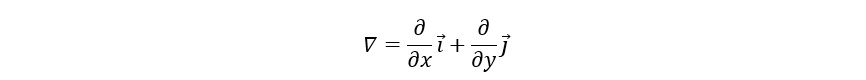

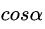







![[字符串]替换空格](https://img-blog.csdnimg.cn/490fdf4bce1c4744ade62df836bb736e.png?x-oss-process=image/watermark,type_d3F5LXplbmhlaQ,shadow_50,text_Q1NETiBAQWxzb25fQ29kZQ==,size_20,color_FFFFFF,t_70,g_se,x_16#pic_center)
