红黑树
- 红黑树概述
- 红黑树性质
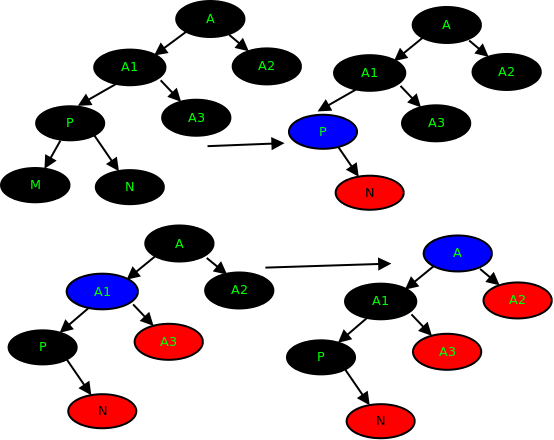
- 红黑树的插入
- 代码实现
红黑树概述
红黑树(Red Black Tree)是一种自平衡二叉查找树,是在计算机科学的中用到的一种数据结构,典型的用途是实现关联数组,红黑树和AVL树类似,都是在进行插入和删除操作时通过特定操作保持二叉查找树的平衡,从而获得较高的查找性能
它虽然是复杂到,但它的最坏情况运行时间也是非常良好的,并且在实践中是高效的:它可以在O(log n)时间内做查找,插入和删除,这里的n是树中元素的数目
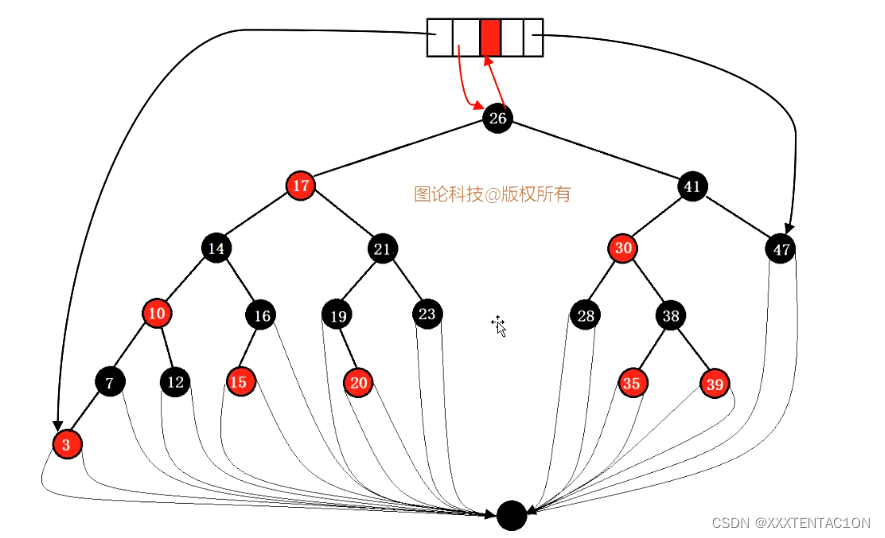
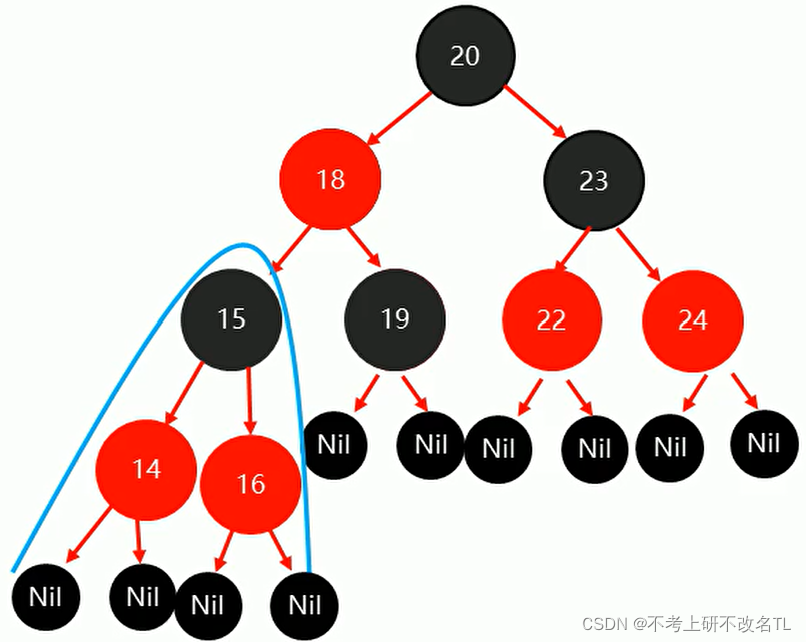
红黑树性质
红黑树是每个结点都带有颜色属性的二叉查找树,颜色是红色或黑色,在二叉查找树强制一般要求以外,对于任何有效的红黑树我们增加了如下的额外要求:
- 性质1 每个结点是红色或黑色
- 性质2 根节点是黑色
- 性质3 每个叶结点(NIL)是黑色
- 性质4 每个红色结点的两个子结点都是黑色(从每个叶子到根的所有路径上不能有两个连续的红色结点)
- 性质 5 从任一结点到其每个叶子的所有路径都包含相同数目的黑色节点
这些约束强制了红黑树的关键性质:从根到叶子的最长的可能路径不多与最短的可能路径的两倍长,结果是这个树大致是平衡的,因为操作比如插入、删除和查找某个值的最坏情况时间都要求与树的高度成正比例,这个在高度上的理论上限允许红黑树在最坏情况下都是高效的,而不同于普通的二叉查找树
是性质 3 导致路径上不能有两个连续的红色节点确保了这个结果,最短的可能路径都是黑色节点,最长的可能路径有交替的红色和黑色节点,因为根据性质 4 所有最长的路径都有相同数目的黑色节点,这就表明了没有路径能多于任何其他路径的两倍长
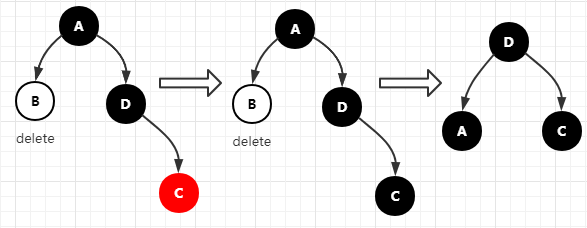
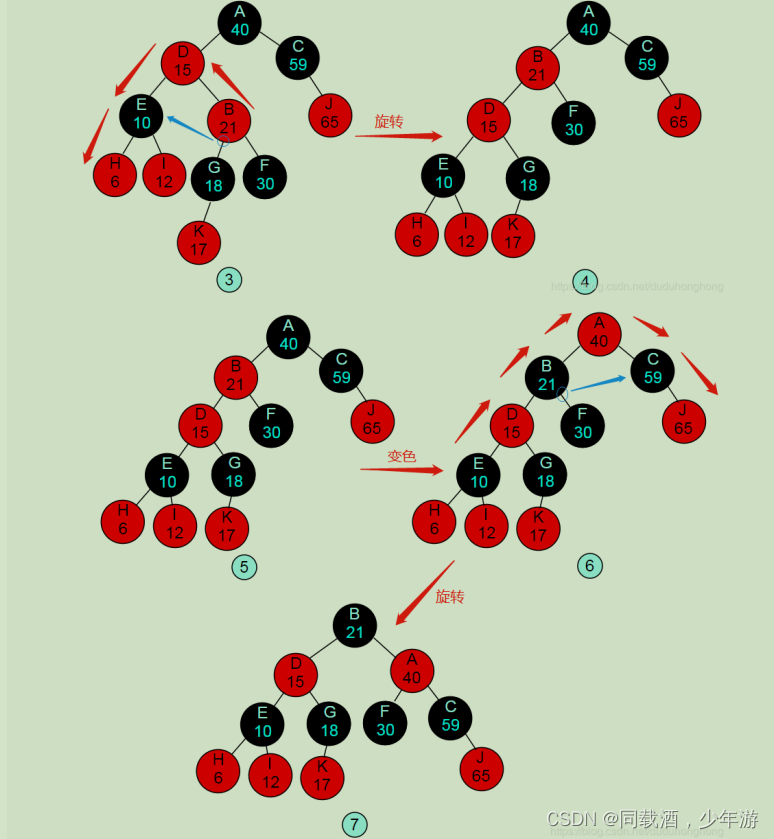
红黑树的插入
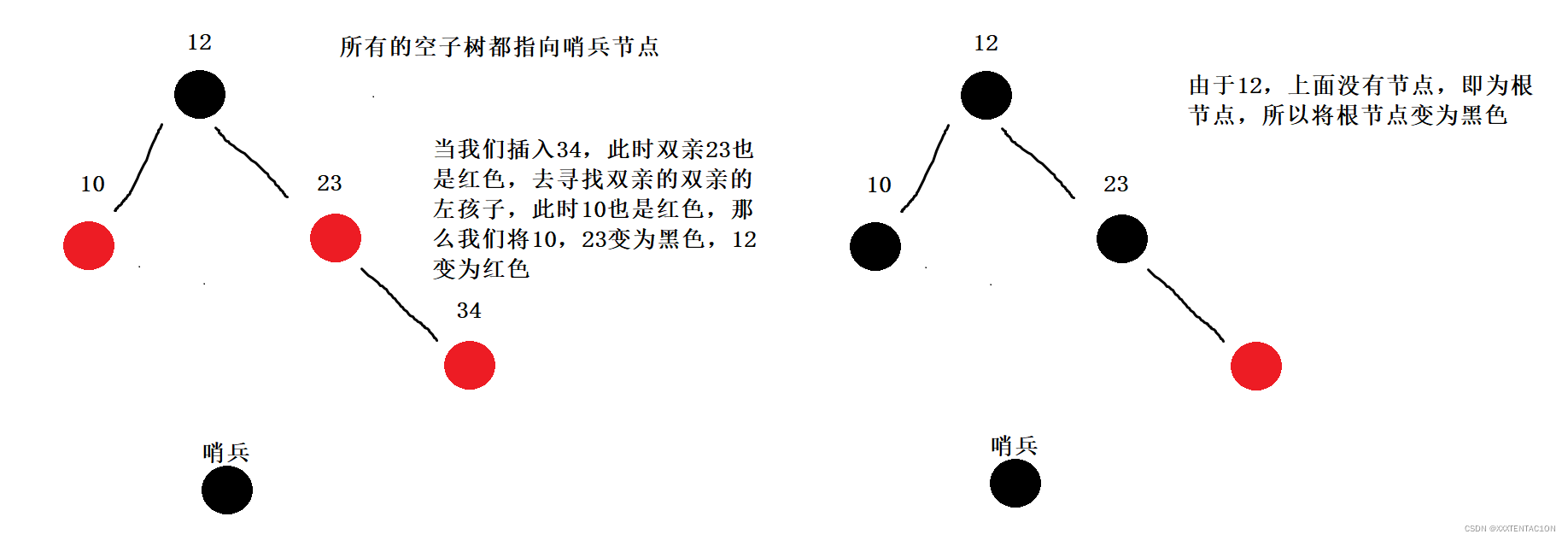
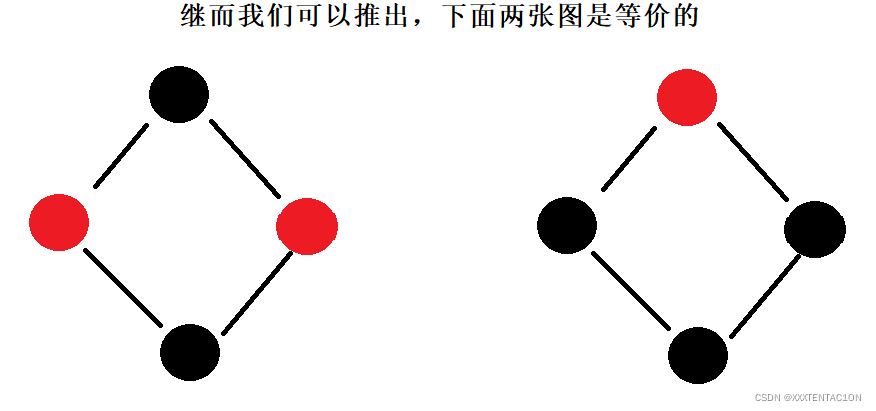
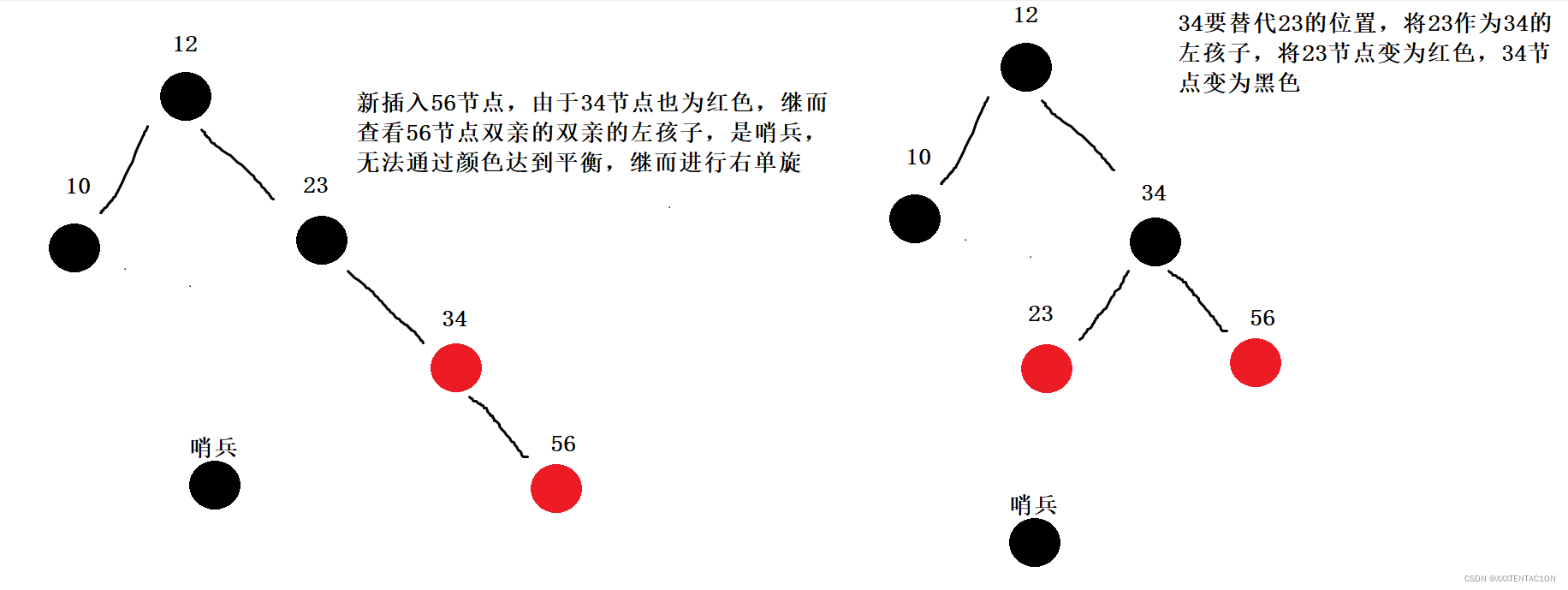
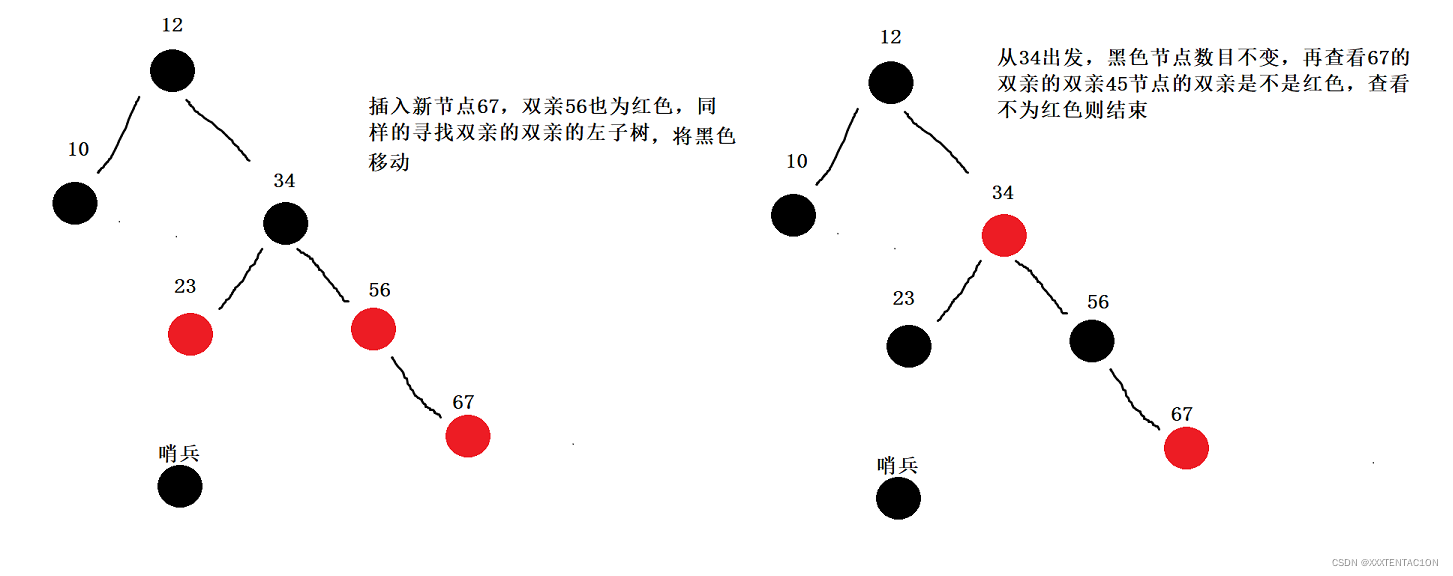
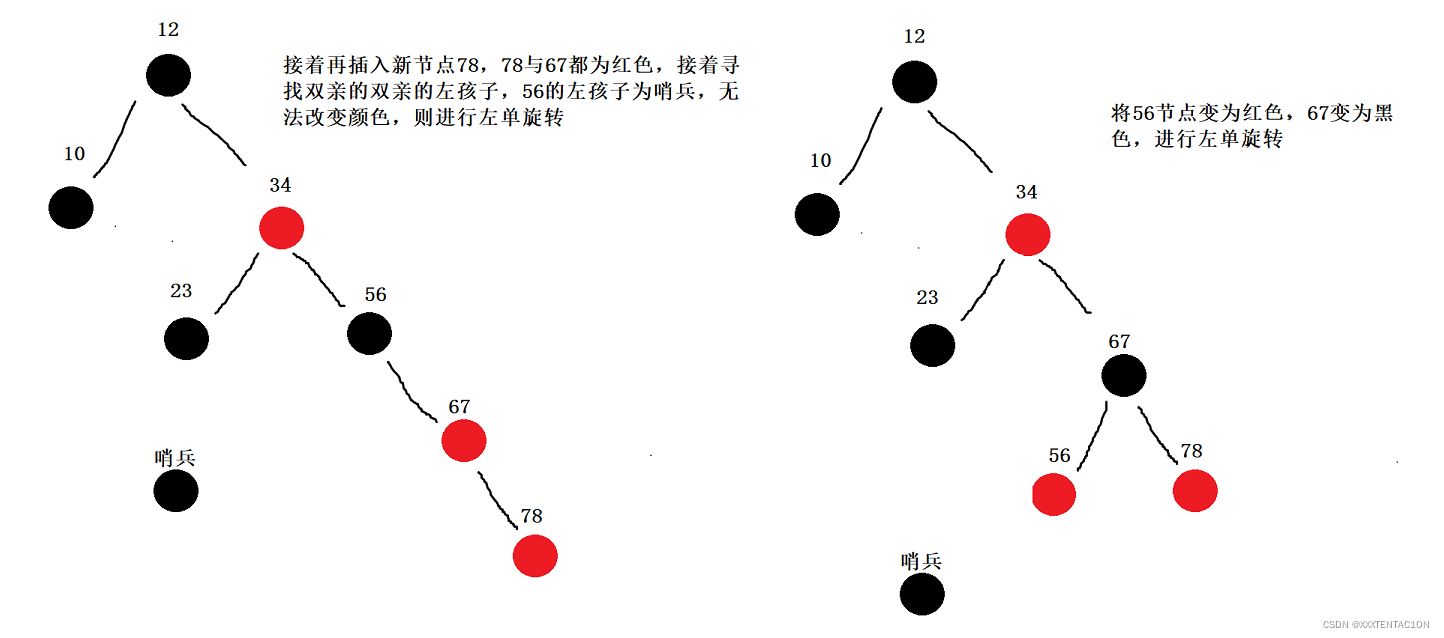
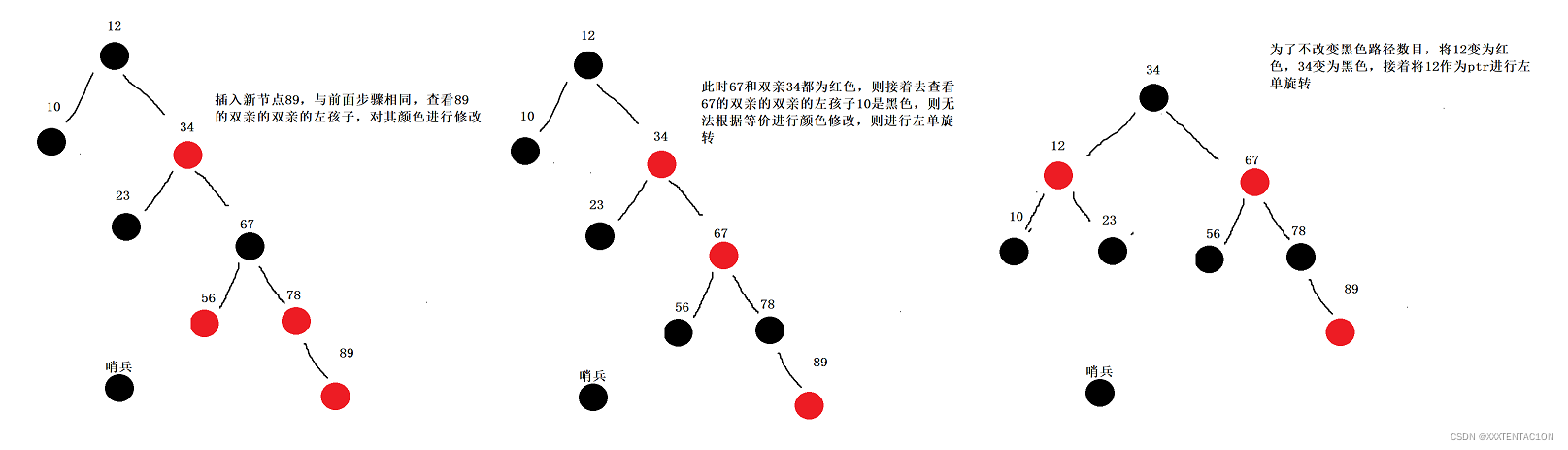
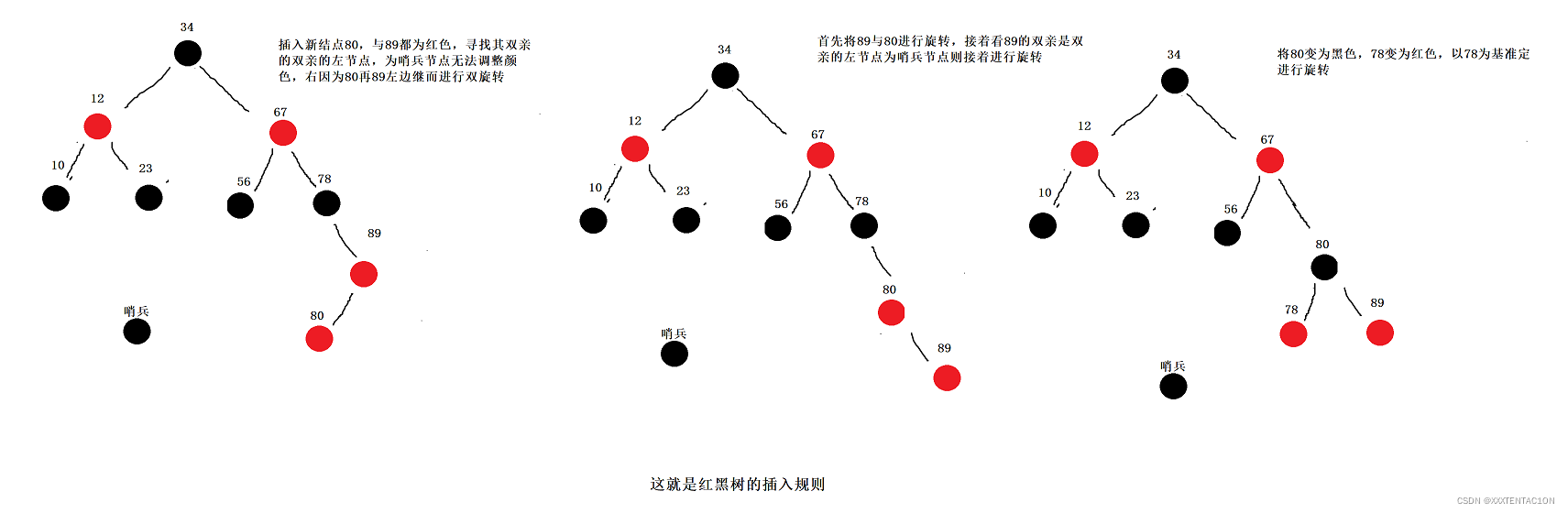
代码实现
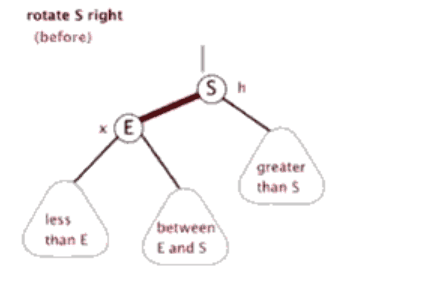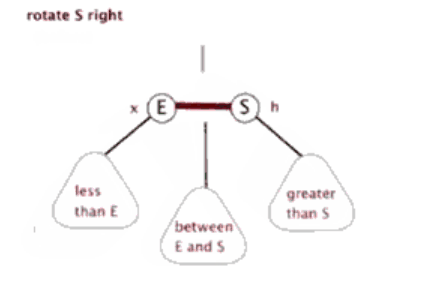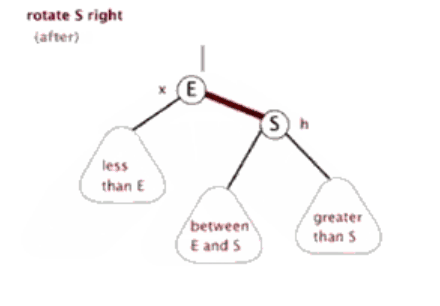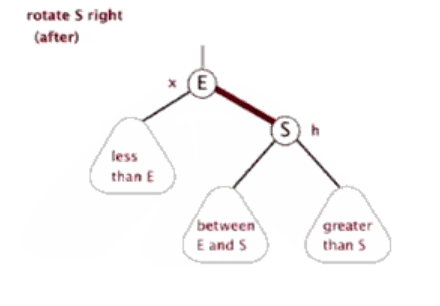
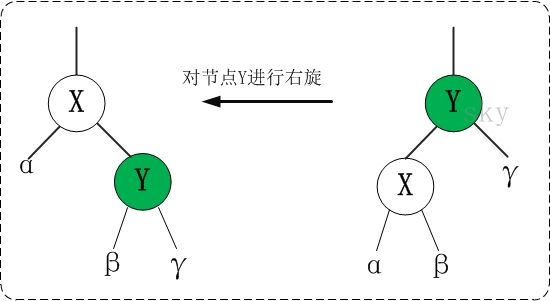
红黑树的左右单旋的代码与AVL树是一致的,根据上面的规则来实现红黑树的插入
typedef enum { RED = 0, BLACK = 1 }ColorType;typedef int KeyType;
typedef struct rb_node
{rb_node* leftchild;rb_node* parent;rb_node* rightchild;ColorType color; //AVL int balanceKeyType key;
}rb_node,*RBTree;rb_node* Buynode();
static rb_node* Nil = Buynode(); //哨兵节点rb_node* Buynode()
{rb_node* s = (rb_node*)malloc(sizeof(rb_node));if (s == nullptr) exit(1);memset(s, 0, sizeof(rb_node));s->rightchild = Nil;s->leftchild = Nil; //新节点左右孩子都指向哨兵s->color = RED;return s;
}
rb_node* MakeRoot(KeyType kx) //建根
{rb_node* root = Buynode();root->color = BLACK;root->key = kx;return root;
}void RotateLeft(rb_node*& tree, rb_node* ptr)
{rb_node* newroot = ptr->rightchild;newroot->parent = ptr->parent;if (newroot->leftchild != nullptr){newroot->leftchild->parent = ptr;}ptr->rightchild = newroot->leftchild;newroot->leftchild = ptr;if (ptr == tree){tree = newroot;}else{if (ptr->parent->leftchild == ptr){ptr->parent->leftchild = newroot;}else{ptr->parent->rightchild = newroot;}}ptr->parent = newroot;
}
void RotateRight(rb_node*& tree, rb_node* ptr)
{rb_node* newroot = ptr->leftchild;newroot->parent = ptr->parent;ptr->leftchild = newroot->rightchild;if (newroot->rightchild != nullptr){newroot->rightchild->parent = ptr;}newroot->rightchild = ptr;if (ptr == tree){tree = newroot;}else{if (ptr->parent->leftchild == ptr){ptr->parent->leftchild = newroot;}else{ptr->parent->rightchild = newroot;}}ptr->parent = newroot;
}void PassRBTree(rb_node*& tree, rb_node* p)
{rb_node* _X = nullptr;for (; p != tree && p->parent->color == RED;){if (p->parent->parent->rightchild == p->parent) //is right{_X = p->parent->parent->leftchild;if (_X->color == RED){_X->color = BLACK;p->parent->color = BLACK;p->parent->parent->color = RED;p = p->parent->parent;}else{if (p->parent->leftchild == p) //我爹在双亲右边,我在双亲左边,是个折线{p = p->parent;RotateRight(tree, p); //先右单旋}p->parent->color = BLACK;p->parent->parent->color = RED;RotateLeft(tree, p->parent->parent); //左单旋转}}else{_X = p->parent->parent->rightchild;if (_X->color == RED){_X->color = BLACK;p->parent->color = BLACK;p->parent->parent->color = RED;p = p->parent->parent;}else{if (p->parent->rightchild == p) {p = p->parent;RotateLeft(tree, p);}p->parent->color = BLACK;p->parent->parent->color = RED;RotateRight(tree, p->parent->parent); }}}tree->color = BLACK;
}bool Insert(rb_node*& tree, KeyType kx)
{if (tree == nullptr){tree = MakeRoot(kx);return true;}rb_node* pa = nullptr;rb_node* p = tree;while (p != nullptr && p->key != kx){pa = p;p = kx < p->key ? p->leftchild : p->rightchild;}if (p != nullptr && p->key == kx) return false;p = Buynode();p->key = kx;p->parent = pa;if (kx < pa->key){pa->leftchild = p;}else{pa->rightchild = p;}PassRBTree(tree, p); //回溯return true;
}