发表于我的博客网站(prajna.top): http://prajna.top/doc/2/175
什么是红-黑二叉树?
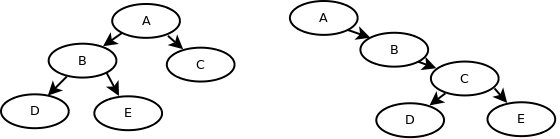
红-黑二叉树首先是一颗二叉树,它具有二叉树的所有性质,是一种平衡二叉树。普通二叉树在生成过程中,容易出现不平衡的现象,即使是使用随机算法生成二叉树,也是有一定概率生成不平衡的二叉树. 如下图所示 :
为了解决二叉树的不平衡问题,“大牛”们终于研究出了 红-黑二叉树(red-black binary tree),它总是生成像左图那样的平衡二叉树。
红-黑二叉树的数据结构
1)叶子节点(leaf child),和 内部节点(internal node)
红黑二叉树的每个节点都增加了2个指针,叫做 leaf child,它永远存在,而且永远都是 child,原二叉树节点,叫做 internal node。
2) 左旋,右旋, 重新着色(recolor)
左旋,右旋, 重新着色(recolor) 是红-黑二叉树的三个基本操作。
3) 规则
3.1) 根节点和 叶子节点(leaf child) 节点必须是黑节点, 内部节点(internal node)非黑即红。
3.2) 从根节点开始到每条子路径的叶子节点(leaf child),所有的黑节点数目相同。
3.3) 红节点的父亲节点必须是黑节点。
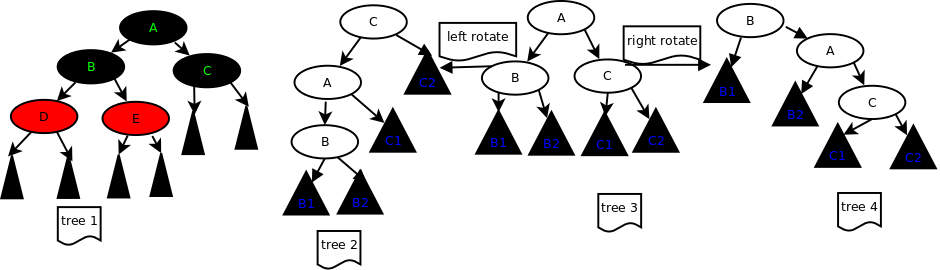
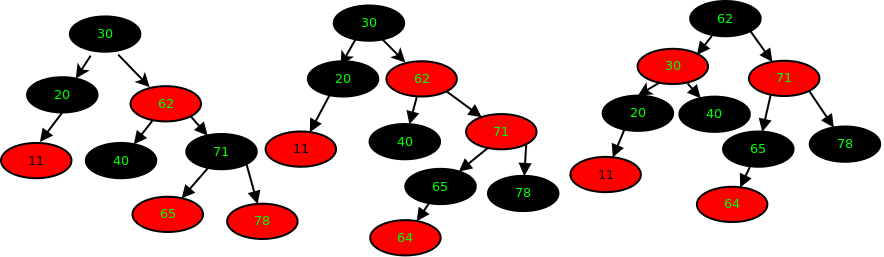
tree 1是一个标准的红-黑树,每条的路径的黑节点数量都是 3。 tree 2和 tree 4是 tree 3 分别左旋,右旋后的结果。
recolor 操作,设想一下树 tree 1,可以把B节点 改变成红色,D和E改变成黑色,这颗红-黑树同样成立,这个操作就是 recolor。
红-黑二叉树的设计思想
如果不了解红-黑树的设计思想,死套相应的操作规则,是件很头疼的事情,知其然而不知其所以然,也是工程师的大忌。可惜,在网上找了不少资料,都介绍红-黑树的工作流程。在这里,我大胆地猜想一下红黑树的设计思想。
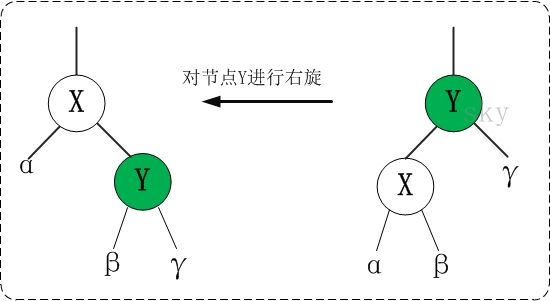
红-黑树的设计思想应该是,利用 红-黑这两种节点颜色来追踪二叉树的平衡状况, 重新着色(recolor)这个操作就是动态刷新各节点颜色,如果发现树开始出现不平衡状况,就使用 左旋(left rotate)或者右旋(right rotate)来改变树的结构。 把图(tree 2) 和(tree 3) 反过来看,它们都是不平衡树,对 (tree 2)进行右旋,或对(tree 4)进行左旋都能得到(tree 3)这样的平衡树。 左旋的实质是增加左树的高度而减少右树的高度,右旋反之。 这样交替运用这三个操作,我们就可以构建一颗平衡的二叉树。
插入
通过上面对设计思想的分析,插入的工作流程就非常简单了。
首先分析 父亲节点 和 叔叔节点的颜色,判断“父亲”和“叔叔”的势力是否平衡。如果平衡,则直接插入,然后进行recolor 操作,继续最踪插入后的情况。否则把"爷爷这颗子树"(父亲节点,爷爷节点 和 叔叔节点)左(右)旋以后再插入。
如何判断"爷爷"这颗子树是否平衡呢?
这就是红-黑树的核心了,通过 "父亲"与"叔叔"的颜色来判断。如果他们同时为红色或者黑色,那么"爷爷"这颗子树是平衡的。否则,就不平衡。需要进行旋转操作来平衡
这两者的势力。
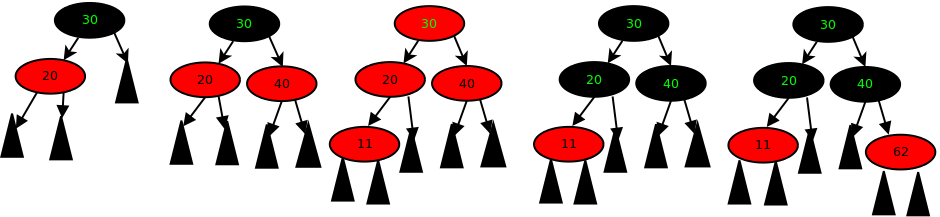
按照 红-黑树的规则,根节点 30 必须是黑色,然后,我们插入 20,为了不违反各分支,黑节点数相等的原则,20必须是红色,接着再插入 红色节点40,so good, so far. 现在 插入 节点11。现在问题出来了,按照红节点必要有黑父亲的规则, 11 和 20 出现了冲突, 这种情况下,需要进行 recolor 操作: 20 和 40 调整为黑色,同时把 11 的爷爷 30 调整为红色,这样可以保证 30 这颗子树的黑节点数目不变。 如果 30 的父亲节点恰好也是红色,需要执行 插入红色节点 30,如果 30的父亲是黑节点,调整结束,如果 30是根节点根据规则,把它改成 黑节点,此时,各分支节黑点数 +1变成了2,数目仍然相等。如果插入的数据是平衡的,我们只需要重复执行,上述操作,插入红节点,recolor。
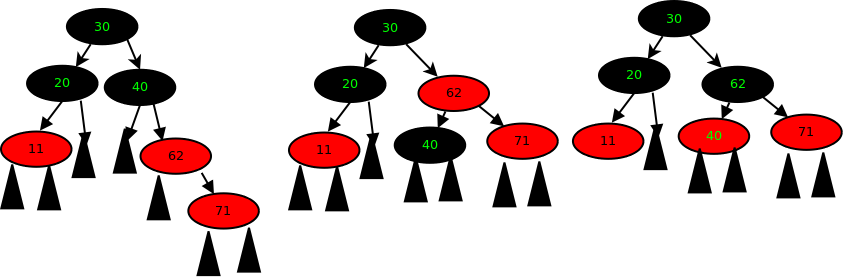
继续插入 71, 发现 71的父亲 62 这个节点没有兄弟节点,很明显以71的爷爷40作为根节点子树,已经不平衡了,因为,平衡的情况应该是,62 有一个 红色的兄弟节点——这样的话,我们只需要递归执行 recolor 即可。 可惜,62没有兄弟,于是,左旋一下 (40-62-71) 这颗树,左旋以后, 黑色根节点40变成了孩子节点,需要把的黑色上提,同新的根节点62交换颜色,以保证 黑色节点数目不变。 就这样交替执行下去,我们就会得到一颗平衡的二叉树。
继续 插入 65,recolor 40, 71, 62这三个节点。 OK,我们继续插入 78,64, 当插入64需要 recolor 65, 78 71 三个节点。 recolor 以后, 71 与 62同为红色节点,违反了规则,此时,执行一个递归算法,把71当成一个新接点插入。 现在让我们来插入新节点 71,由于 62 与 20颜色不相同, 30为根节点的这颗树不平衡,需要左一个 左旋的操作。
同时 62 与30 互换颜色。 现在,71的父亲为根节点,递归结束,71 插入成功。
上面的演示,包含了所有的插入的基本情况。 总结一下:
1)插入的新节点,总是红节点。
2) 如果 插入出现红节点冲突:
1)父亲,叔叔都是红节点,表明树处于平衡状态,执行重新着色(recolor)操作,否则进行旋转操作。
2) 把新的爷爷节点(子树根节点)当成一个新的节点, 插入该树。 重新执行,插入新节点的操作。
具体的 伪代码,很多地方都右介绍,我就不多说了。 伪代码里面,把插入的各种状况分得很细——一些变化的中间状态,也当成了一个插入状态,只是编程的需要,理论上,
从我们的刚才的分析中可以得出,实际的插入就2个状态,平衡 or 不平衡——通过父亲与叔叔的颜色来判断。 平衡就recolor,不平横就 rotate. 千万不要被代码的分析给迷惑住了。
删除
首先执行的是二叉树的通用删除方法, 找被删节点M的子节点C来替换它,而不是直接删除M,M被C替换后,删除C即可!这样就把一个删除 父亲节点的问题,转变成了删除子节点的问题。 子节点C的选择原则是, 取右分支最左边,或者 左分支最右边的。 这样,我们只需要研究 子节点C的删除情况,子节点C 最多有一个孩子节点(C 是最左边或者最右边)。
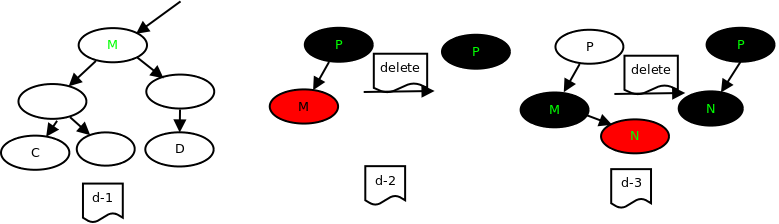
如下图 d-1所示,要删除M节点,可以先用 C或者D替换M,然后,在删除C或者D。
红-黑二叉树删除节点,最大的麻烦是要保持 各分支黑色节点数目相等。 因为是删除,所以不用担心存在颜色冲突问题——插入才会引起颜色冲突。
1) 直接删除。
1.1) M节点是红节点,直接删除。图 d-2. M不可能带有其它子节点——如子节点为黑,则违反黑节点数原则,为红,则违反“颜色”原则。
1.2) M节点是黑节点带有红色子节点直接用子节点,则recolr 子节点为黑,替换M。
2) M节点无子节点,且与 P 节点同为黑色。
如果删除M则分支 P的黑节点数肯定 少一个,如果M有子节点,就直接用子节点顶上来(情况1)。现在只右考察一下M的兄弟N,如果它是红色节点,那就好办了,
利用 插入时 reclor逆操作,把红节点变成黑节点,保持黑节点数目不变。
先是进行一个左旋, 把红节点当作新的根节点,然后,recolor,此时,P为红,M和N1则为黑, 最后,再此 recolor, 把 M和N1变红,P 变黑,现在可以直接删除M了。
其实,仔细观察一下,会发现它是 插入 recolor的逆过程。
OK,现在我们利用 红节点变黑, 删除了一个黑节点。保持了黑节点数目不变的原则。
如果 M 节点的兄弟节点是也是黑节点怎么办呢?
这种情况,把M的兄弟S recolor 为红,P节点分支减少一个 黑节点数, 然后,再把 P节点当作当前节点,递归"删除",直到其它分支,也都recolor一个黑节点为红节点,使黑节点数保持相同。
:“删除”加了引号,这个删除不是指从树中移除——这个过程是在最开始通过子节点替换完成的——而是指递归 recolor 一个黑节点。
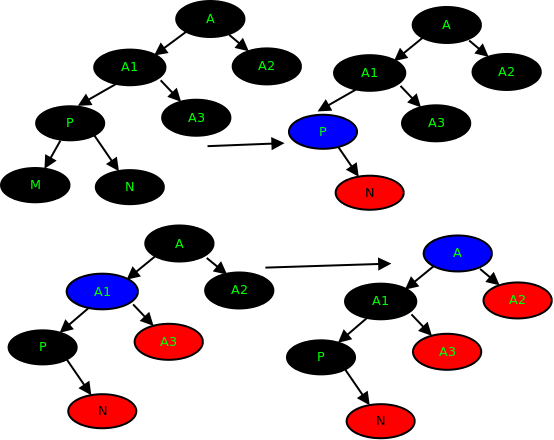
先recolor M的兄弟N,然后,“删除” 当前节点P, recolor p的兄弟 A3, 再"删除" A1,recolor A2,依次递归向上,每个分支减少一个 黑节点。
这里的 递归删除 根节点 P,并不是真正意义上面的删除,不同于删除节点M,只是为了重用代码的结构而已。
一些文章的伪代码里面,把删除也分成了好多种情况,其实 理论上就三种。 1) 直接删除。 2) 旋转,recolor 红节点成黑节点。 3) 递归,recolor 黑节点为红节点。
后记
这两天研究 红-黑树,到网上查了好多资料,都是讲述的操作流程,没有文章讲一下算法的思想。看得人一头雾水。我花了些时间,仔细研究了一下,感觉还是蛮简单的。
真的很佩服算法的设计者。写出来供大家研究一下。
参考资料
1) http://en.wikipedia.org/wiki/Red%E2%80%93black_tree
2) 算法导论。
3) google 了一些文章。