目录
一、定义
二、插入
三、删除
四、全部代码
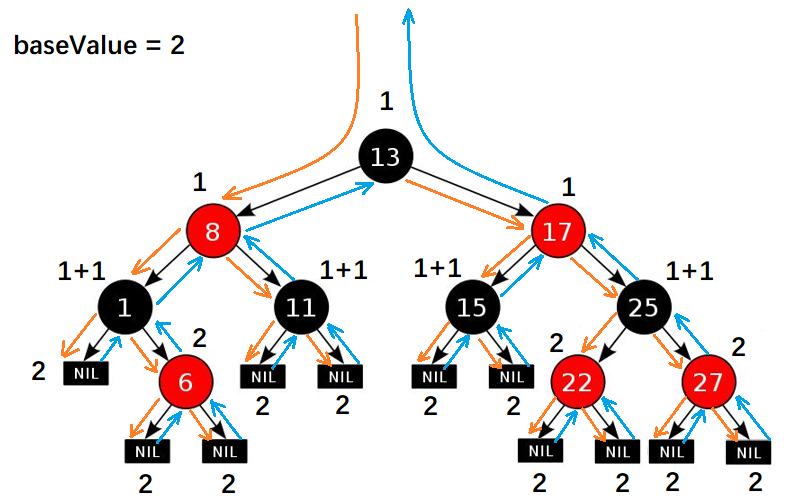
五、颜色效果
一、定义
红黑树是特殊的平衡二叉树,具有以下特性:
1、根节点的颜色是黑色
2、节点颜色要么是黑色、要么是红色
3、如果一个节点的颜色是红色,则它的子节点必须是黑色,即不能有2个连续的红色节点
4、每个叶子节点都是黑色(这里的叶子节点是为空的叶子节点)
5、从一个节点到该节点的叶子节点的所有路径上都包含相同数量的黑色节点
通过上面的定义,可以看到红黑树本质上还是一颗二叉查找树,所以,对红黑树的插入删除操作都可以分为两阶段来完成,首先,将红黑树看成一颗普通的二叉查找树完成插入删除操作,然后,通过旋转(左旋、右旋)以及颜色调整来使得操作后的树满足红黑树的所有特性即可。
二、插入
说明:以下的讨论,在如下前提下进行:插入的节点为S(son),S的父亲节点为F(father),F的父亲节点为G(grandfather),而F的兄弟节点为U(uncle),并且F为G的左儿子。(F为G的右儿子对称操作即可)
Step 1:执行二叉搜索树插入逻辑
Step 2:将插入的节点着色为红色
我们希望这次插入尽可能不破坏红黑树的性质,这样我们就可以不用进行额外的调整操作!所以,根据特性(5),我们显然不能将节点涂成黑色,因为这样所有经过点S的路径的黑色节点都多了一个,就破坏了特性(5),所以我们将S的颜色首先着色为红。
Step 3:进行适当得旋转以及颜色调整
如果插入节点的父节点是红,那么违反了特性(3),所以需要进行调整,共有三个case
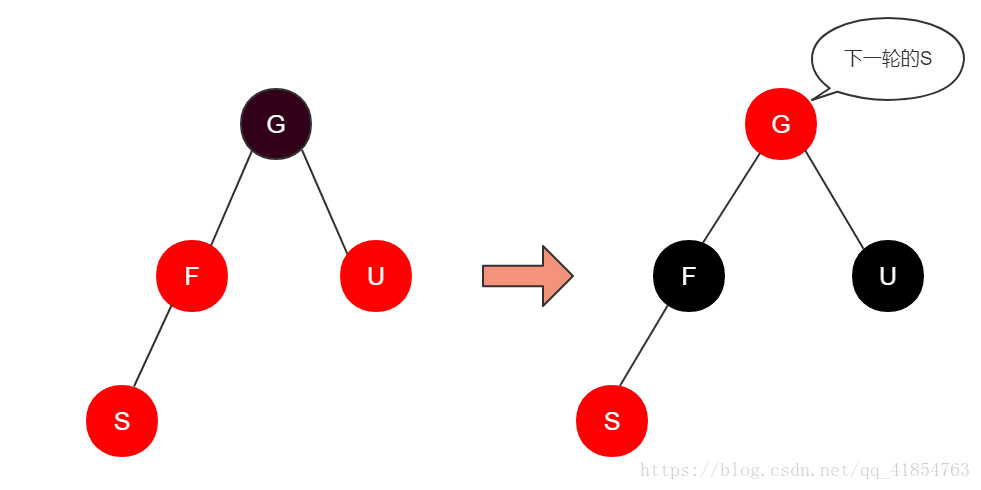
case 1:F为红,U为红
操作:将F以及U设置为黑,G设为红,并将G看成新插入的节点(即下一轮的S),递归操作。
原因:这个操作实际是想将红色往根处移动。将红色往上移了一层,并不会打破红黑树的特性,不断的把红色往上移动,当移动到根时,直接将根设置为黑色,就完全符合红黑树的性质了。
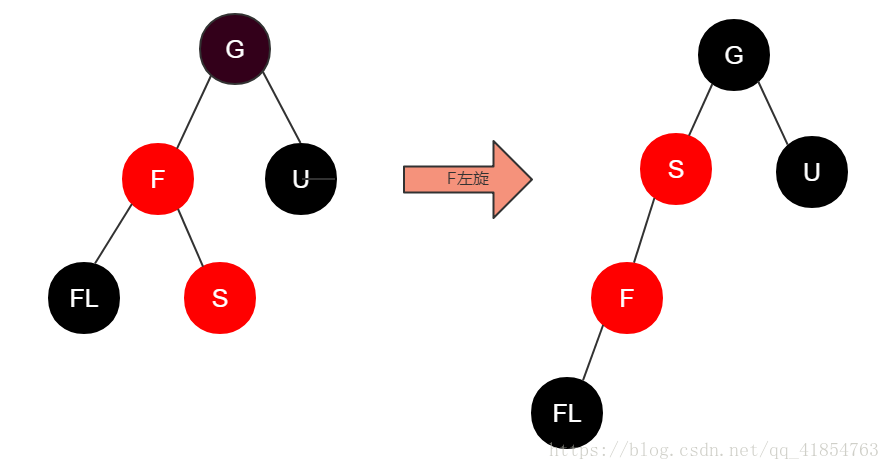
case 2:F为红,U为黑,并且,S为F的右儿子
操作:将F左旋,并把F看成新加入的节点(即下一轮的S),继续后面的判断。
原因:这个操作是为了将这一case转换为case 3
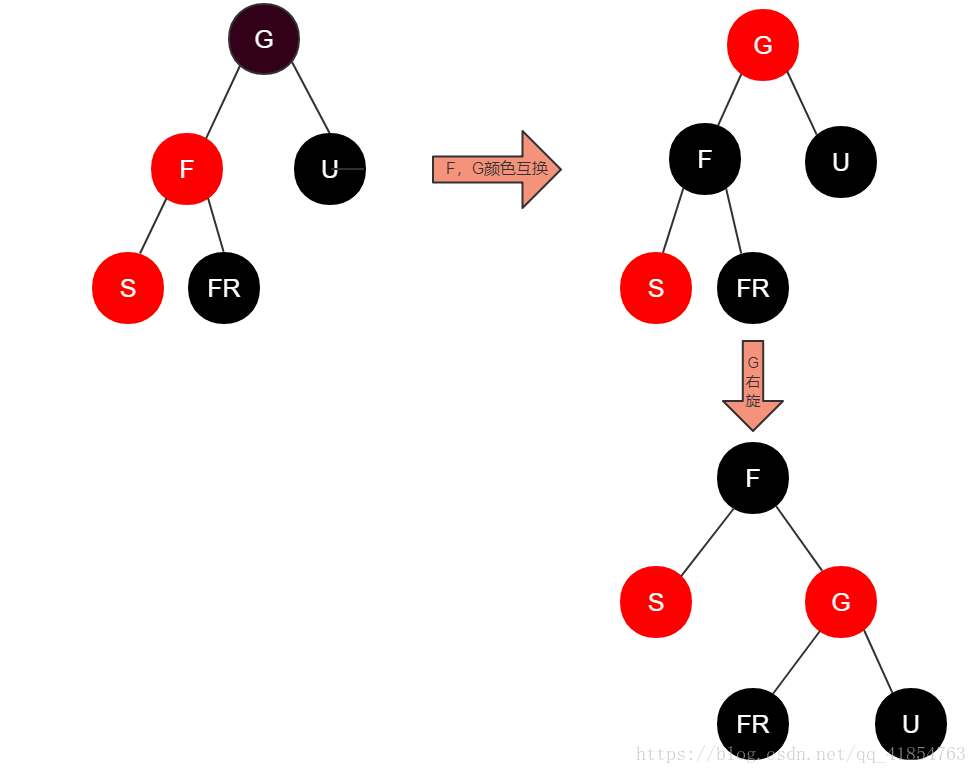
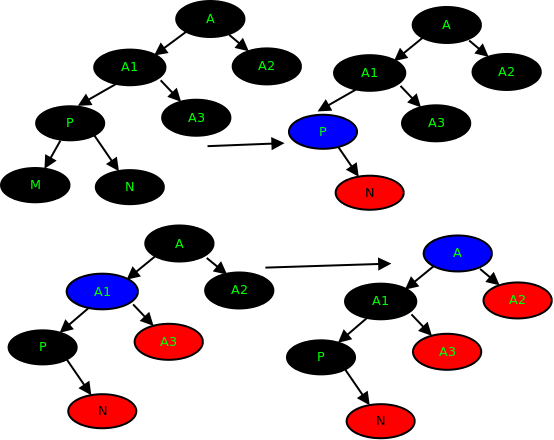
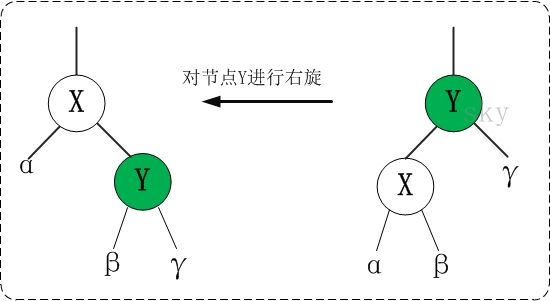
case 3:F为红,U为黑,并且,S为F的左儿子
操作:先将F设为黑,G设为红,然后G右旋。这样操作后,就完全符合红黑树的性质。
原因:G与F颜色互换,对左边路并没有影响,不过,对于右边路来说,由于G变为了红,其实少了一个黑,因此,将G右旋,使得黑色的F变为新的G,这样,就为右边路加回去了一个黑,而左边路只是损失了一个红,并不影响红黑树的平衡,这样操作后将会完全符合红黑树的性质,之所以说是完全符合,因为原来G的地方是个黑色节点,后来用了黑色的F去代替了G,对于G往上的层来说,并没有发生颜色变化,自然就是平衡的,所以,经过这一步的操作,红黑树恢复所有特性。
三、删除
说明:S的父亲节点为P,S的兄弟节点为B,B的左儿子为BL,B的右儿子为BR,且S为P的左儿子。(S为P的右儿子对称操作即可)
step 1:进行二叉查找树的删除操作
我们假设想要删除的节点是X,找到的替代节点为Y(选择方式是X的右子树的最小点),那么我们可以将Y的值拷贝到X,然后将这个Y删除,将Y删除,也会需要有一个人顶替现在的Y的位置,我们设为S,接下来的讨论就会围绕着S展开。
step 2:红黑树性质判断
由于我们将Y删除了,并且用S代替了Y的位置,如果Y原来是红色的,那么并不会破坏红黑树的颜色平衡,我们不需要额外的操作,删除成功!如果Y是黑色的,那么相当于经过Y的路径(现在是经过S)都会少了一个黑。那么我们怎么把这个黑弥补回来呢?那就是给S再加上一个黑,用来弥补删除Y而损失的那个黑。这时候,相当于S节点拥有了两个颜色,违反了特性(2),所以,我们现在想办法把这个多出来的黑色删除掉!
如果原来S是红色的,那么我们直接不要S的红色,将S设置为黑色即可,因为丢弃红色是不会打破红黑树的颜色平衡的,我们这一操作是安全的。可是,如果S原来就是黑色呢?那就要看S是不是根了,如果是根,将黑色丢弃了也没啥,相当于所有的路径都减少了一个黑,也是不影响平衡的,最糟糕的情况在于S原来是黑,且不是根,这时候,我们就要进行一些旋转以及颜色调整来恢复红黑树的特性了!
step 3:旋转以及颜色调整
共有四个case:
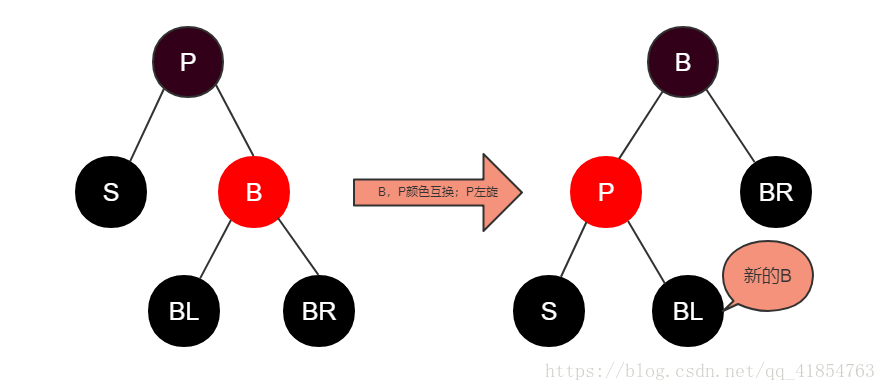
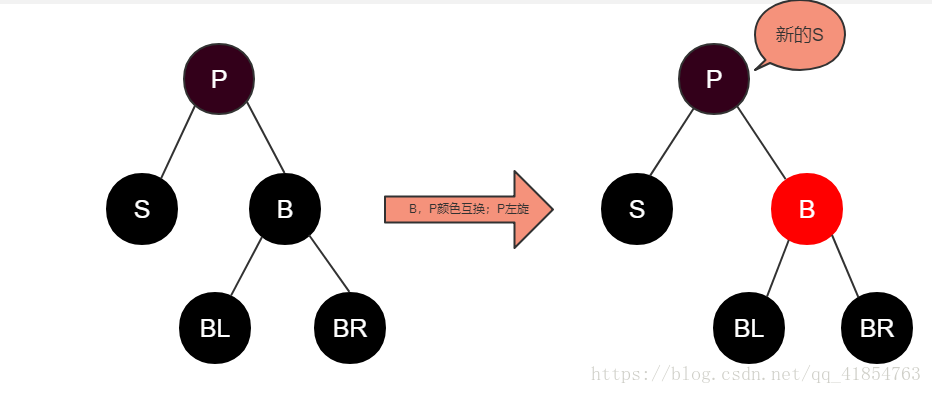
Case 1: S是“黑+黑”,且B为红。
操作:将P设为红,B设为黑,然后将P左旋,这时S获得了新的B,用新的B进行后续的判断
原因:在这种情况下,我们可以得到P必定为黑,并且BL & BR 也都为黑。由于我们想要左旋(左旋的目的是让S有新的B,从而转化为后面的case 2 or 3 or 4,进行下一步的操作),而又不能破坏红黑树的平衡,所以,将P设为红,B设为黑。
Case 2:S是“黑+黑”,且B为黑,并且BL BR也都是黑。
操作:将B设为红,并且让P为新的S,进行新一轮的递归。
原因:我们的目的就是想让多余的黑往上走,这时候,把这个多余的黑给到P,左边路的黑是不变的,而右边路多了一个,为了平衡,恰好BL BR都是黑,所以我们直接把B设为红就好啦,这样,黑就上浮到了P,将P看作新的起点(S),递归后面的操作就好啦~!
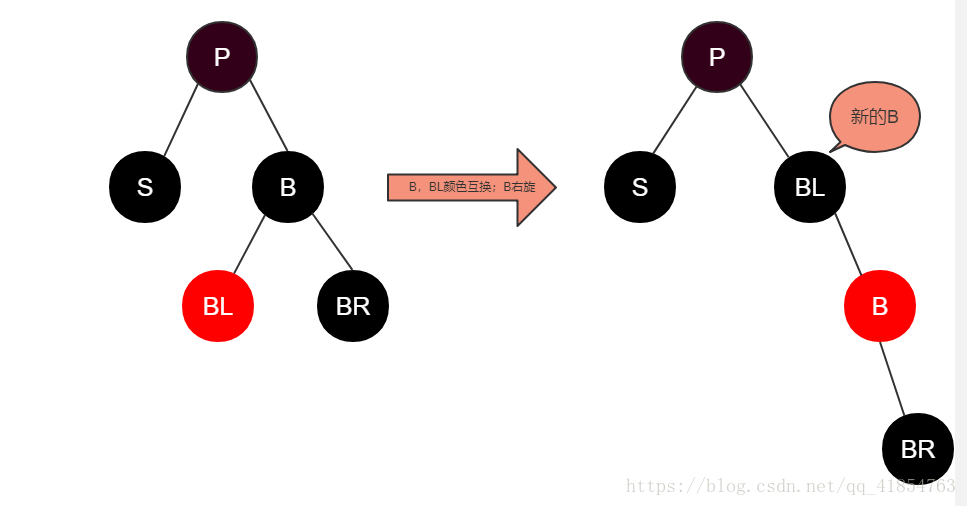
Case 3:S是“黑+黑”,且B为黑,并且BL为红,BR为黑。
操作:将B设为红,BL设为黑,然后B右旋
原因:这个操作是为了转换到case 4。B和BL的颜色互换也是为了平衡。
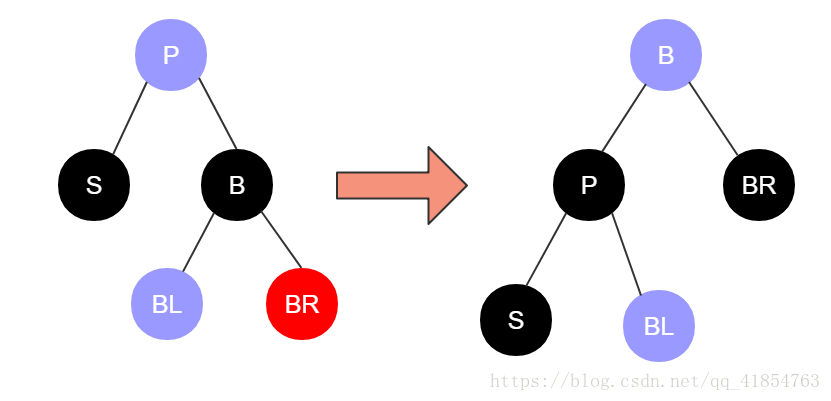
Case 4:S是“黑+黑”,且B为黑,并且BR为红,(P、BL任意颜色)。
操作:将P的颜色给到B,将P设为黑,将BR设为黑,对P左旋,最后将S设置为root以结束循环。
原因:我们将P的颜色给到B,然后将P左旋,这时候,不管P初始是什么颜色,首先是BL变成了P的儿子,而这里我们不关心BL的颜色,所以,必须要把P设置为黑色,这样即使BL为红色也不会破坏红黑树,而将P设置为黑色,对于左边路,都多了一个黑色,为了保证颜色平衡,正好把S中多余的那个黑丢掉啦。还有一点,不管P的初始颜色,左旋之后,右边路少了一个黑,为了补回来,我们让BR由红变黑就好啦!
(注:蓝色表示任意颜色)
四、全部代码
红黑树节点
package com.mzp.tree.rb;/*** 红黑树节点*/
public class RedBlackTreeNode {public static boolean Red = false;public static boolean Black = true;//节点颜色private boolean color;private int data;private RedBlackTreeNode left;private RedBlackTreeNode right;private RedBlackTreeNode parent;public RedBlackTreeNode(int data){this.data = data;color = Red;}public boolean isColor() {return color;}public void setColor(boolean color) {this.color = color;}public int getData() {return data;}public void setData(int data) {this.data = data;}public RedBlackTreeNode getLeft() {return left;}public void setLeft(RedBlackTreeNode left) {this.left = left;}public RedBlackTreeNode getRight() {return right;}public void setRight(RedBlackTreeNode right) {this.right = right;}public RedBlackTreeNode getParent() {return parent;}public void setParent(RedBlackTreeNode parent) {this.parent = parent;}
}
红黑树
package com.mzp.tree.rb;import java.util.LinkedList;
import java.util.Queue;/*** 红黑树*/
public class RedBlackTree {//根节点private RedBlackTreeNode root;public static void main(String[] args) {RedBlackTree tree = new RedBlackTree();tree.insert(12);tree.insert(1);tree.insert(9);tree.insert(2);tree.insert(0);tree.insert(11);tree.insert(7);tree.insert(19);tree.insert(4);tree.insert(15);tree.insert(18);tree.insert(5);tree.insert(14);tree.insert(13);tree.insert(10);tree.insert(16);tree.insert(6);tree.insert(3);tree.insert(8);tree.insert(17);tree.delete(12);tree.delete(1);tree.delete(9);tree.delete(2);tree.delete(0);tree.delete(11);tree.delete(7);tree.delete(19);tree.delete(4);tree.delete(15);tree.delete(18);tree.delete(5);tree.delete(14);tree.delete(13);tree.delete(10);tree.delete(16);//tree.delete(6);//tree.delete(3);//tree.delete(8);//tree.delete(17);System.out.println("层级");levelTraversal(tree.root);System.out.println();System.out.println("前序");recursivelyPreTraversal(tree.root);System.out.println();System.out.println("中序");recursivelyInTraversal(tree.root);System.out.println();System.out.println("后序");recursivelyPostTraversal(tree.root);}/*** 插入节点* @param data* @return*/public RedBlackTreeNode insert(int data){RedBlackTreeNode insert = new RedBlackTreeNode(data);if(root == null){root = insert;setBlack(insert);}else{RedBlackTreeNode parent = null;RedBlackTreeNode node = root;while(node != null){parent = node;if(node.getData() >= data){//左子树node = node.getLeft();}else{//右子树node = node.getRight();}}//跳出循环则说明找到插入位置if(parent.getData() >= data){parent.setLeft(insert);}else{parent.setRight(insert);}insert.setParent(parent);//旋转和调整节点颜色保持红黑树平衡insertFix(insert);}return insert;}/*** 旋转和调整节点颜色保持红黑树平衡* @param node 插入节点*/private void insertFix(RedBlackTreeNode node) {while(node.getParent() != null && isRed(node.getParent())){RedBlackTreeNode parent = node.getParent();RedBlackTreeNode grandFather = parent.getParent();if(grandFather.getLeft() == parent){//F为G左儿子的情况RedBlackTreeNode uncle = grandFather.getRight();if(uncle != null && isRed(uncle)){setBlack(parent);setBlack(uncle);setRed(grandFather);node = grandFather;continue;}if(parent.getRight() == node){//插入节点为父节点的右子树//左旋leftRotate(parent);//将旋转后的parent看作插入节点RedBlackTreeNode tmp = node;node = parent;parent = tmp;}setBlack(parent);setRed(grandFather);rightRotate(grandFather);break;}else{//F为G的右儿子的情况,对称操作RedBlackTreeNode uncle = grandFather.getLeft();if(uncle != null && isRed(uncle)){setBlack(parent);setBlack(uncle);setRed(grandFather);node = grandFather;continue;}if(parent.getLeft() == node){//插入位置为父节点的左子树//右旋rightRotate(parent);RedBlackTreeNode tmp = node;node = parent;parent = tmp;}setBlack(parent);setRed(grandFather);leftRotate(grandFather);break;}}setBlack(root);}/*** 删除节点* @param data* @return*/public RedBlackTreeNode delete(int data){RedBlackTreeNode node = query(data);if(node == null){return null;}deleteNode(node);return node;}/*** 查询节点* @param data* @return*/public RedBlackTreeNode query(int data){if(root == null){return null;}RedBlackTreeNode node = root;while(node != null){if(node.getData() == data){return node;}else if(node.getData() >= data){node = node.getLeft();}else {node = node.getRight();}}return null;}private void deleteNode(RedBlackTreeNode node) {if (node == null){return;}//替换节点RedBlackTreeNode replaceNode = null;if(node.getLeft() != null && node.getRight() != null){//存在左右子树RedBlackTreeNode tmp = node.getRight();while(tmp != null){replaceNode = tmp;tmp = tmp.getLeft();}//将替换节点的值放到原本需要删除的节点node.setData(replaceNode.getData());//删除替换节点node = replaceNode;}if(node.getLeft() != null){replaceNode = node.getLeft();}else{replaceNode = node.getRight();}RedBlackTreeNode parent = node.getParent();if(parent == null){root = replaceNode;if(replaceNode != null){replaceNode.setParent(null);}}else{if(parent.getLeft() == node){parent.setLeft(replaceNode);}else{parent.setRight(replaceNode);}if(replaceNode != null){replaceNode.setParent(parent);}}if(isBlack(node)){//replaceNode为了保持平衡,多了一个黑色,需修复removeFix(parent, replaceNode);}}/*** 修复* @param parent* @param node 多了一个黑色*/private void removeFix(RedBlackTreeNode parent, RedBlackTreeNode node) {while(isBlack(node) && node != root){if(parent.getLeft() == node){//S是P的左儿子RedBlackTreeNode brother = parent.getRight();if(isRed(brother)){setBlack(brother);setRed(parent);leftRotate(parent);brother = parent.getRight();}if(brother == null || (isBlack(brother.getLeft()) && isBlack(brother.getRight()))){setRed(brother);node = parent;parent = node.getParent();continue;}if(isRed(brother.getLeft()) && isBlack(brother.getRight())){setRed(brother);setBlack(brother.getLeft());rightRotate(brother);brother = parent.getRight();}brother.setColor(parent.isColor());setBlack(parent);setBlack(brother.getRight());leftRotate(parent);node = root;}else{//S是P的右儿子RedBlackTreeNode brother = parent.getLeft();if(isRed(brother)){setBlack(brother);setRed(parent);rightRotate(parent);brother = parent.getLeft();}if(brother == null || (isBlack(brother.getLeft()) && isBlack(brother.getRight()))){setRed(brother);node = parent;parent = node.getParent();continue;}if(isRed(brother.getRight()) && isBlack(brother.getLeft())){setBlack(brother.getRight());setRed(brother);leftRotate(brother);brother = parent.getLeft();}brother.setColor(parent.isColor());setBlack(parent);setBlack(brother.getLeft());rightRotate(parent);node = root;}}if(node != null){setBlack(node);}}/*** 左旋* @param node*/private void leftRotate(RedBlackTreeNode node) {RedBlackTreeNode right = node.getRight();RedBlackTreeNode parent = node.getParent();node.setRight(right.getLeft());if(right.getLeft() != null){right.getLeft().setParent(node);}node.setParent(right);right.setLeft(node);if(parent == null){root = right;right.setParent(null);}else{right.setParent(parent);if(parent.getLeft() != null && parent.getLeft() == node){parent.setLeft(right);}else{parent.setRight(right);}}}/*** 右旋* @param node*/private void rightRotate(RedBlackTreeNode node) {RedBlackTreeNode left = node.getLeft();RedBlackTreeNode parent = node.getParent();node.setLeft(left.getRight());if(left.getRight() != null){left.getRight().setParent(node);}node.setParent(left);left.setRight(node);if(parent == null){root = left;left.setParent(null);}else{left.setParent(parent);if(parent.getLeft() != null && parent.getLeft() == node){parent.setLeft(left);}else{parent.setRight(left);}}}/*** 设置颜色为黑* @param node*/public static void setBlack(RedBlackTreeNode node) {if(node == null){return;}else{node.setColor(RedBlackTreeNode.Black);}}/*** 设置颜色为红* @param node*/public static void setRed(RedBlackTreeNode node) {if(node == null){return;}else{node.setColor(RedBlackTreeNode.Red);}}/*** 是否是黑色节点* @param node* @return*/public static boolean isBlack(RedBlackTreeNode node){if(node == null){return true;}else{return node.isColor() == RedBlackTreeNode.Black;}}/*** 是否是红色节点* @param node* @return*/public static boolean isRed(RedBlackTreeNode node){if(node == null){return false;}else{return node.isColor() == RedBlackTreeNode.Red;}}/*** 层级遍历* @param root*/public static void levelTraversal(RedBlackTreeNode root){if(root == null){return;}Queue<RedBlackTreeNode> queue = new LinkedList<>();queue.offer(root);while(!queue.isEmpty()){RedBlackTreeNode poll = queue.poll();String color = "Black";if(isRed(poll)){color = "Red";}System.out.print(poll.getData()+"(" + color + ") ");if(poll.getLeft() != null){queue.offer(poll.getLeft());}if(poll.getRight() != null){queue.offer(poll.getRight());}}}/*** 前序遍历* @param node*/public static void recursivelyPreTraversal(RedBlackTreeNode node){if(node == null){return;}String color = "Black";if(isRed(node)){color = "Red";}System.out.print(node.getData()+"(" + color + ") ");recursivelyPreTraversal(node.getLeft());recursivelyPreTraversal(node.getRight());}/*** 中序遍历* @param node*/public static void recursivelyInTraversal(RedBlackTreeNode node){if(node == null){return;}recursivelyInTraversal(node.getLeft());String color = "Black";if(isRed(node)){color = "Red";}System.out.print(node.getData()+"(" + color + ") ");recursivelyInTraversal(node.getRight());}/*** 后序遍历* @param node*/public static void recursivelyPostTraversal(RedBlackTreeNode node){if(node == null){return;}recursivelyPostTraversal(node.getLeft());recursivelyPostTraversal(node.getRight());String color = "Black";if(isRed(node)){color = "Red";}System.out.print(node.getData()+"(" + color + ") ");}
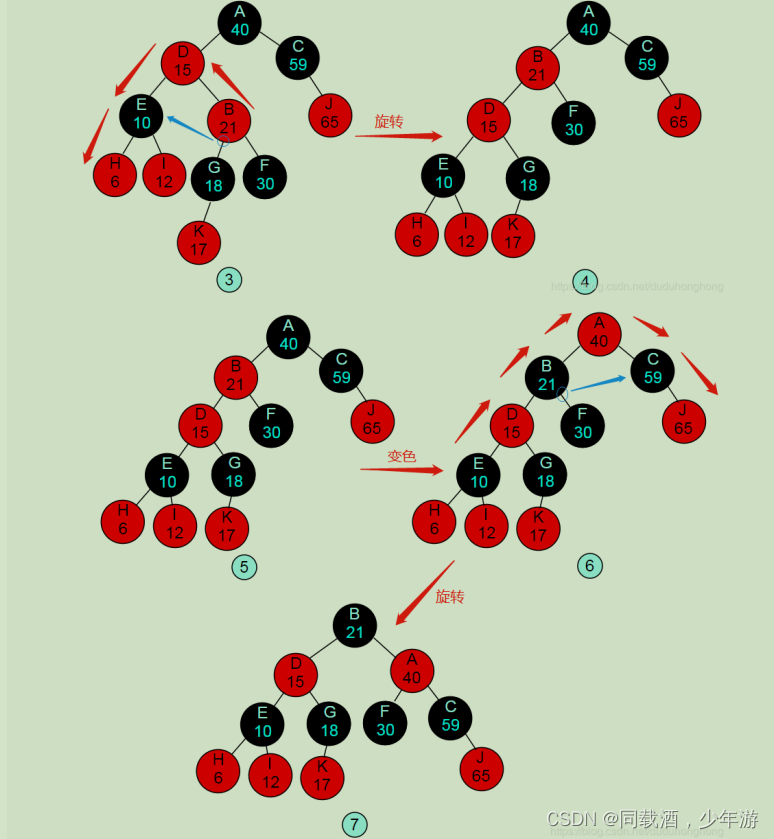
}五、颜色效果
可参考根据红黑树研究记录-实例 - Geek_Ma - 博客园图片验证代码是否正确

参考地址:红黑树理解以及Java实现_一个默默努力的人的博客-CSDN博客_红黑树java
红黑树研究记录-实例 - Geek_Ma - 博客园