【数据结构】--二叉树,红黑树
- 🏆概念
- 🍍定义
- 🍋 术语
- 📝可视化网站
- ☀️二叉树
- ✨ 二叉搜索树
- 🍍定义
- 🍑查找节点
- 🍋插入节点
- 🍅遍历节点
- 🍕 前序排序
- 🧀 后序排序
- 🍟 中序排序
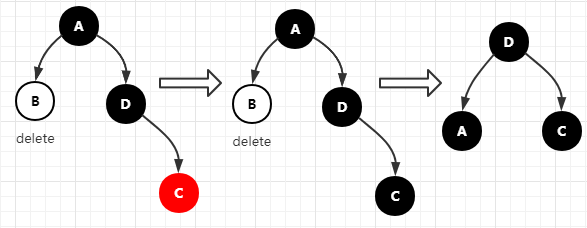
- 🍇删除节点
- 🍖删除无子节点的节点
- 🌺删除有一个子节点的节点
- 🔥删除有两个子节点的节点
- ⭐️时间复杂度分析
- 🐈二分查找算法的
- 🎉缺陷
- ⭐️平衡二叉树(AVL树)
- 🔥 红黑树
- ✌变色
- 🎄左旋
- 🎄右旋
- 🔎参考博客
🏆概念
🍍定义
树:N个节点构成的有限结合,树中有一个称为“根”的特殊节点。其余节点分为互不相交的“子树”。

🍋 术语
- 节点:以图为例,11,20.41 …都是节点。
- 边:节点与节点之间的连线为边。
- 根:树顶端的节点为根节点。一棵树只有一个根节点。
- 节点相对关系: 11是20的子节点;20是11的父节点;29是11的兄弟节点。
- 叶子节点:没有子节点的节点,例如11。
- 度:树中一个节点的孩子个数称为该结点的度,树中节点的最大度数称为树的度。例如:20的度为2;(孩子节点为11,29)
- 高度:从下往上看,从节点到叶子节点的最长路径。从0开始计数。所有叶子节点的高度为0.例如:20节点的高度为:2;
- 深度:从上往下看,从根节点到任意节点的路径长度。从0开始计数。根节点深度为0.例如:29的深度为:2;
- 层次:从上往下看,从1开始计数。根节点层次为1.
有的资料对于高度深度从0还是1开始计数定义不同,可参考树的高度和深度
树的性质
————————————————
版权声明:本文为CSDN博主「UniqueUnit」的原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接及本声明。
原文链接:https://blog.csdn.net/Real_Fool_/article/details/113930623
📝可视化网站
🔎visualgo

🔎usfca

☀️二叉树
树的每个节点最多只能有两个子节点.(二叉树中不存在度大于2的结点);二叉树的子树有左右之分,其次序不能任意颠倒。



✨ 二叉搜索树
🍍定义
在二叉树的基础上,加一个额外的条件,可以得到特殊的二叉树,二叉搜索树
二叉搜索树要求:
- 若左子树不为空,则左子树所有节点的值均小于它的根节点;
- 若右子树不为空,则右子树所有节点的值均大于它的根节点;
- 左右子树为二叉排序树
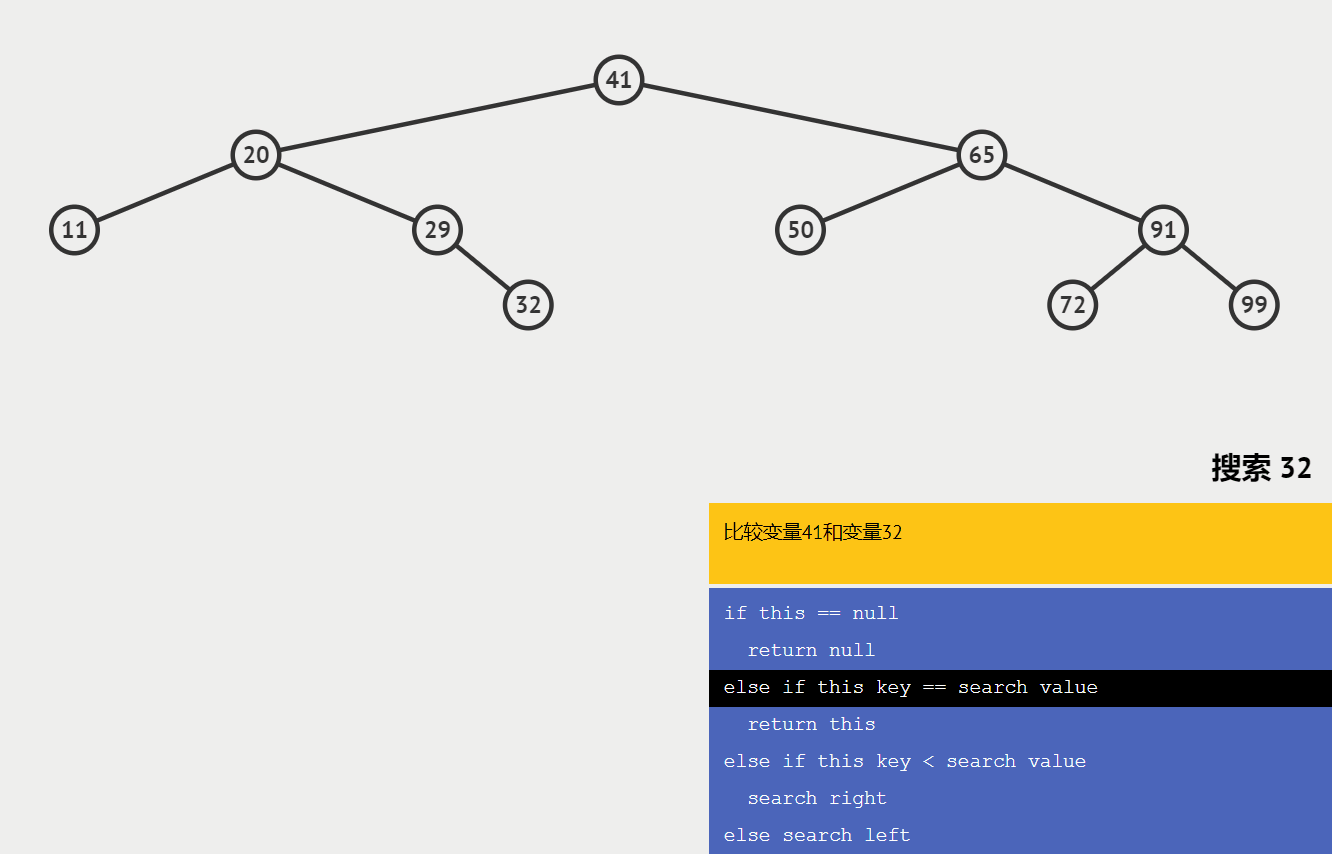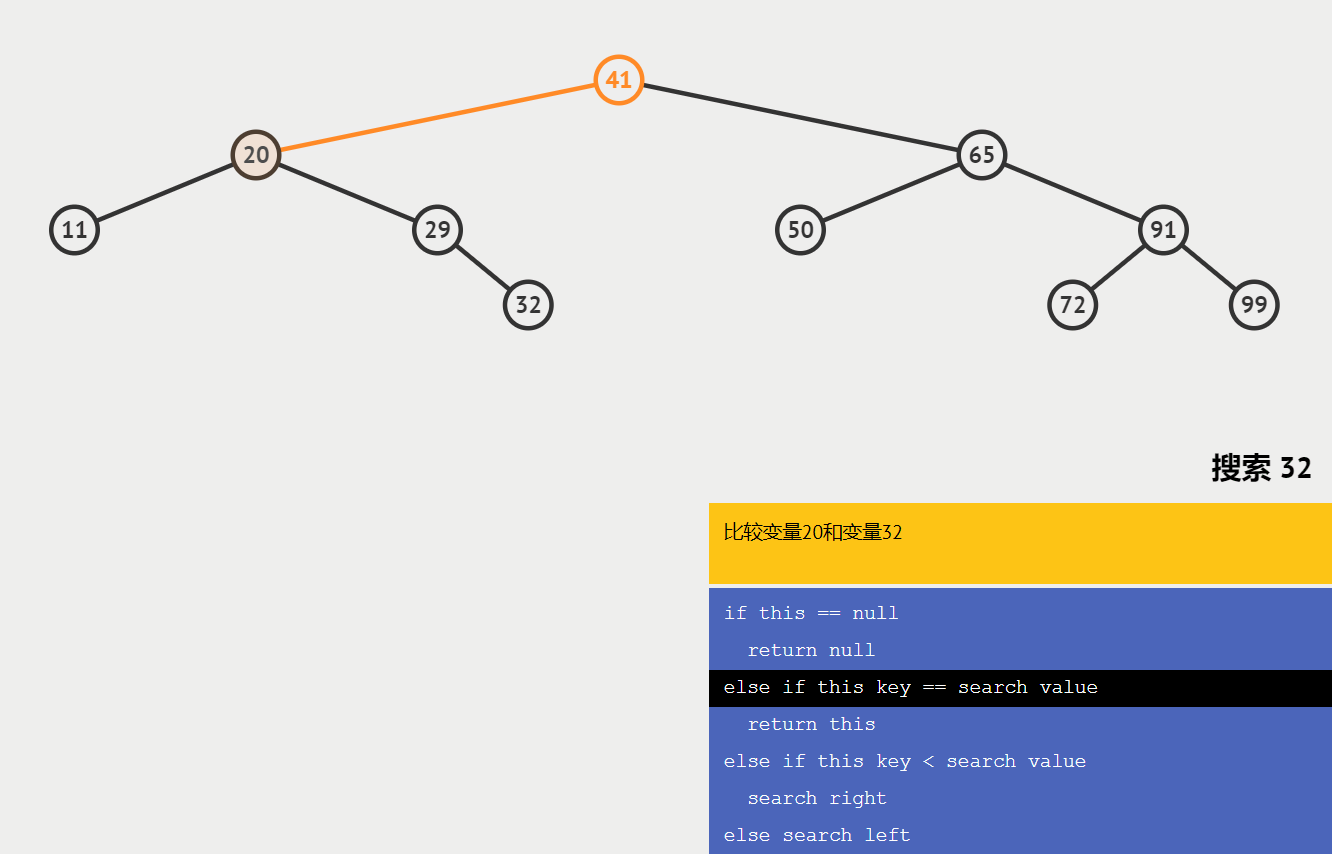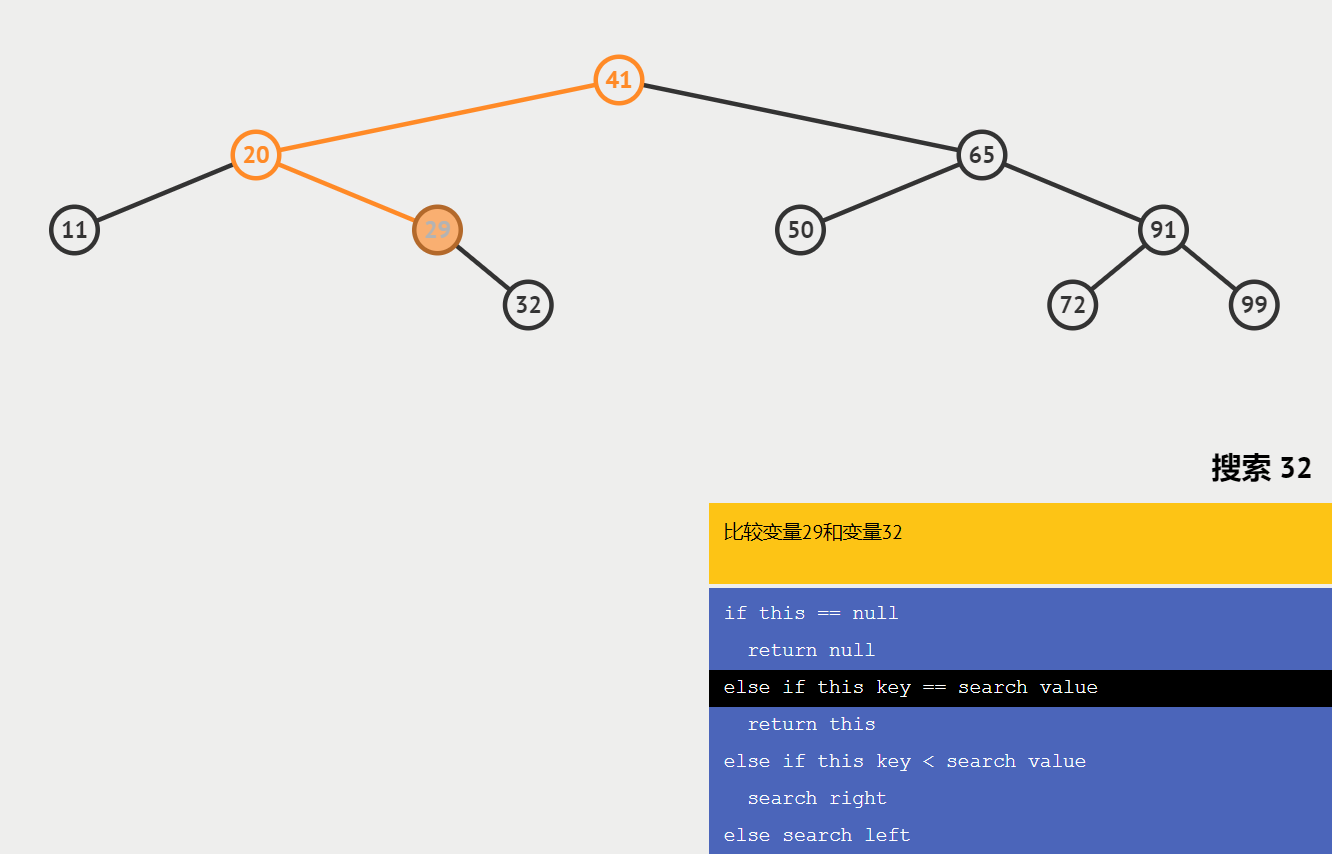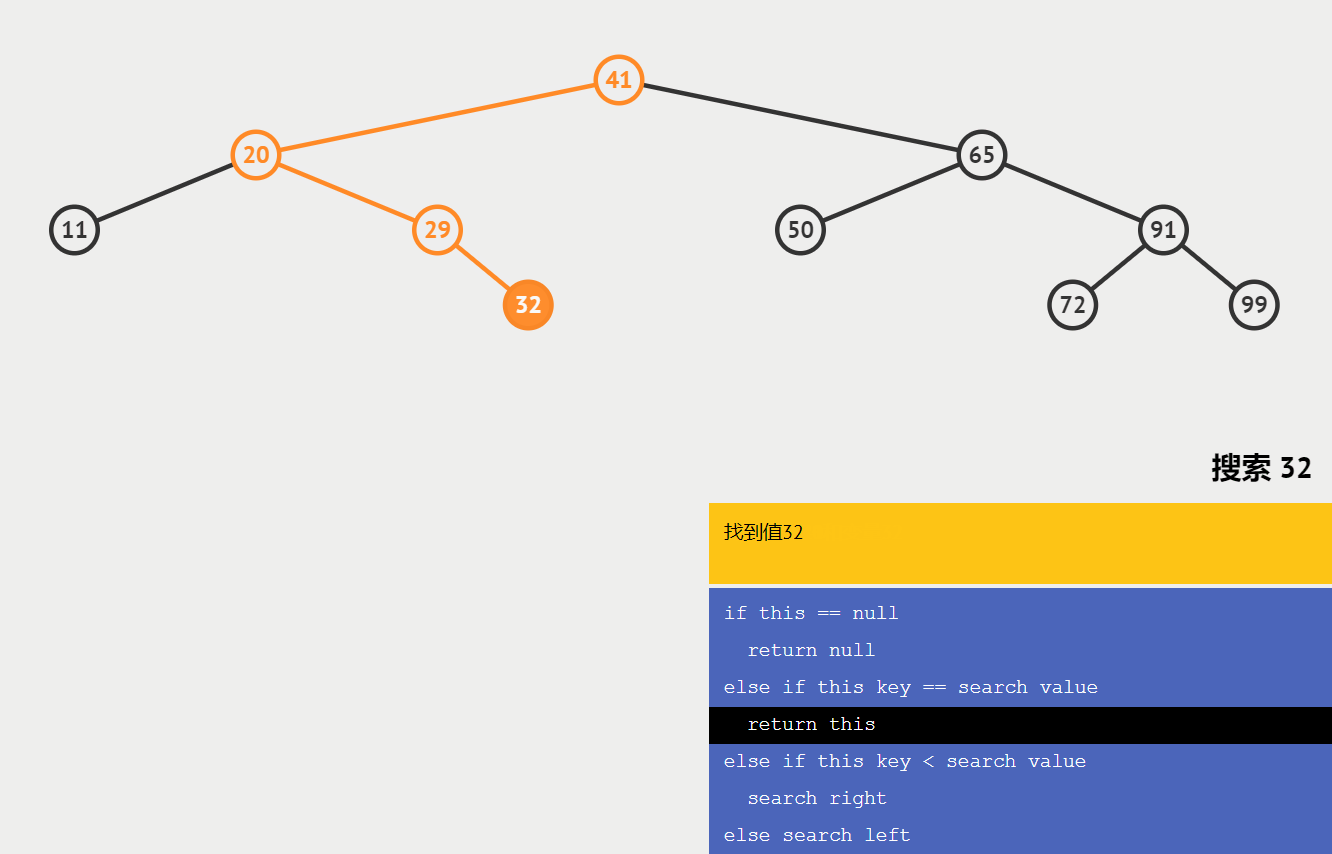
🍑查找节点
查找某个节点,必须从根节点开始查找;
查找值比当前节点值大,则搜索右子树;
查找值等于当前节点值,停止搜索;
查找值小于当前节点值,则搜索左子树;
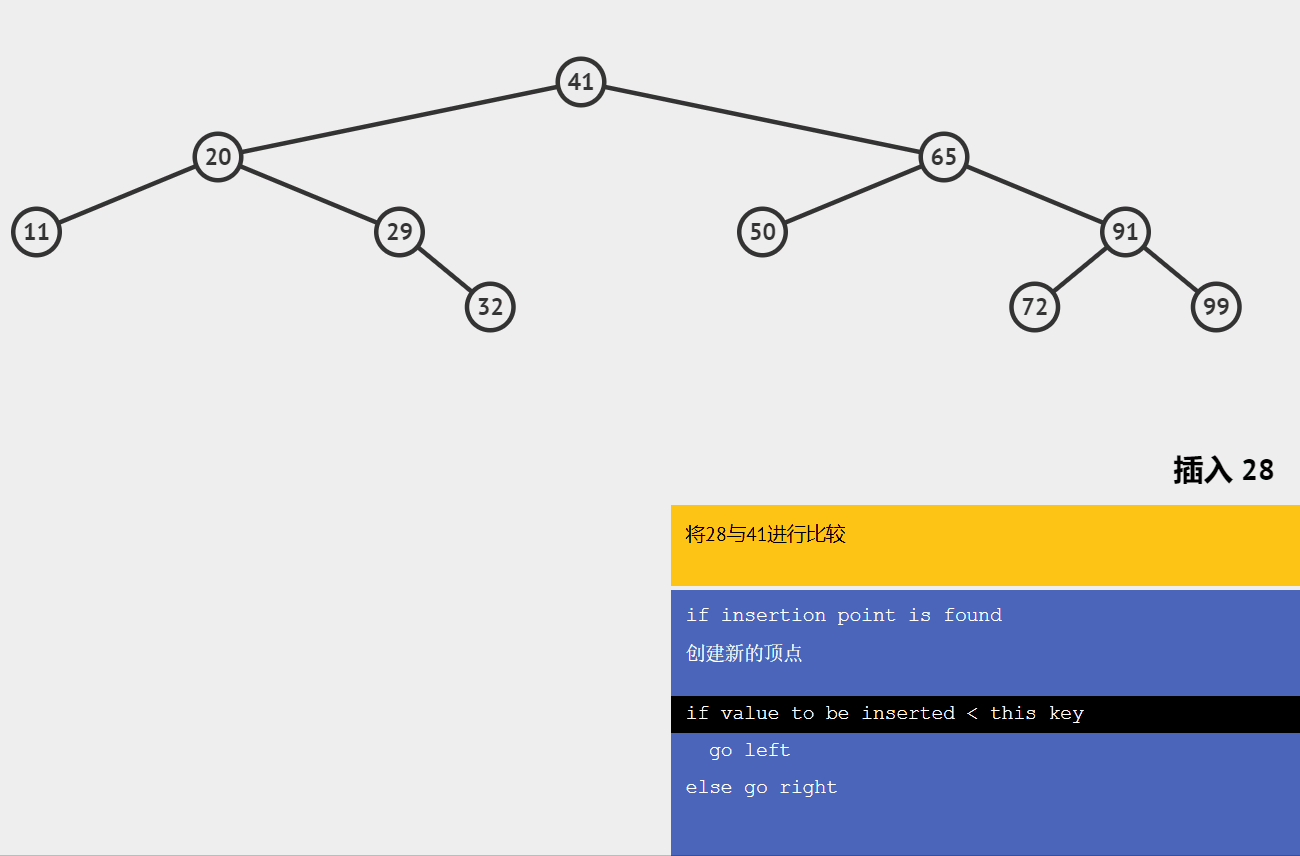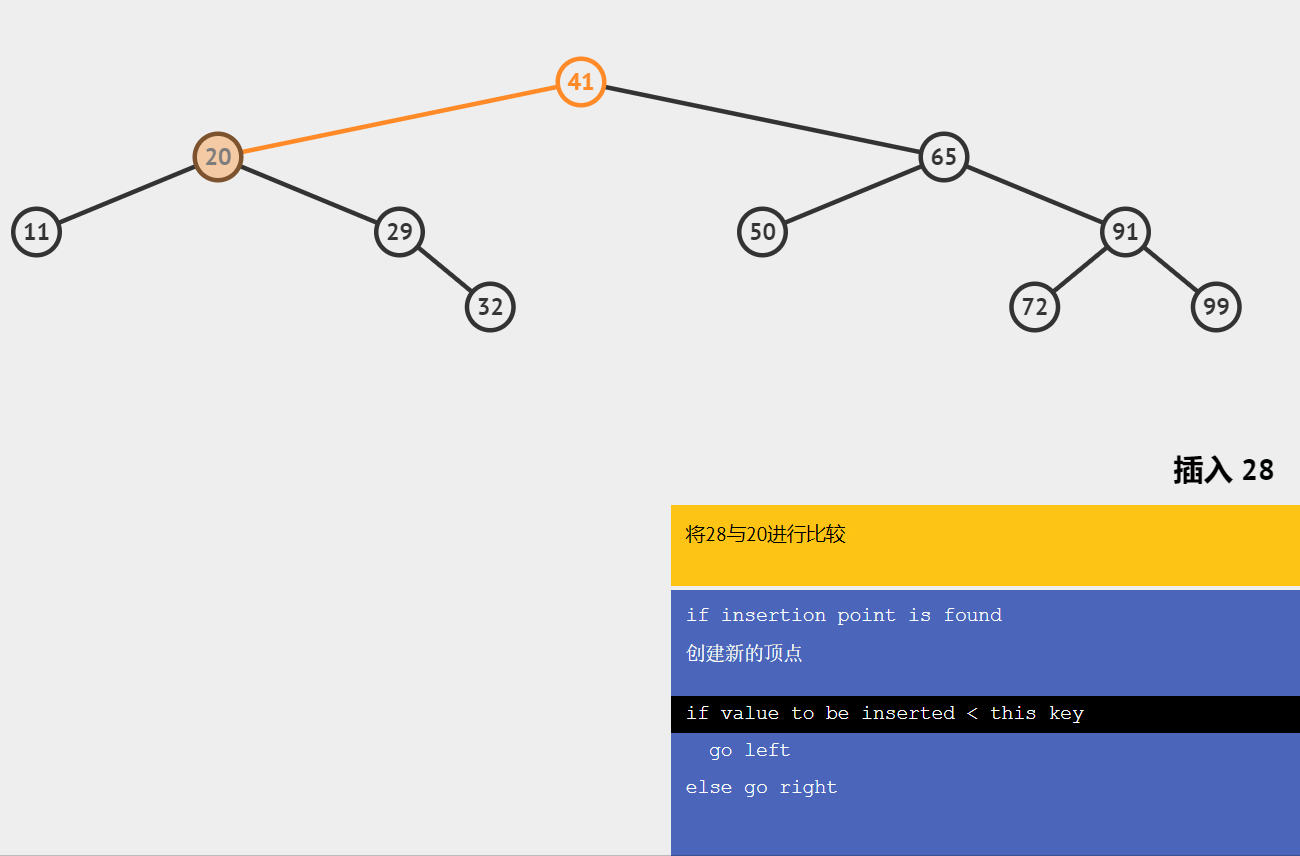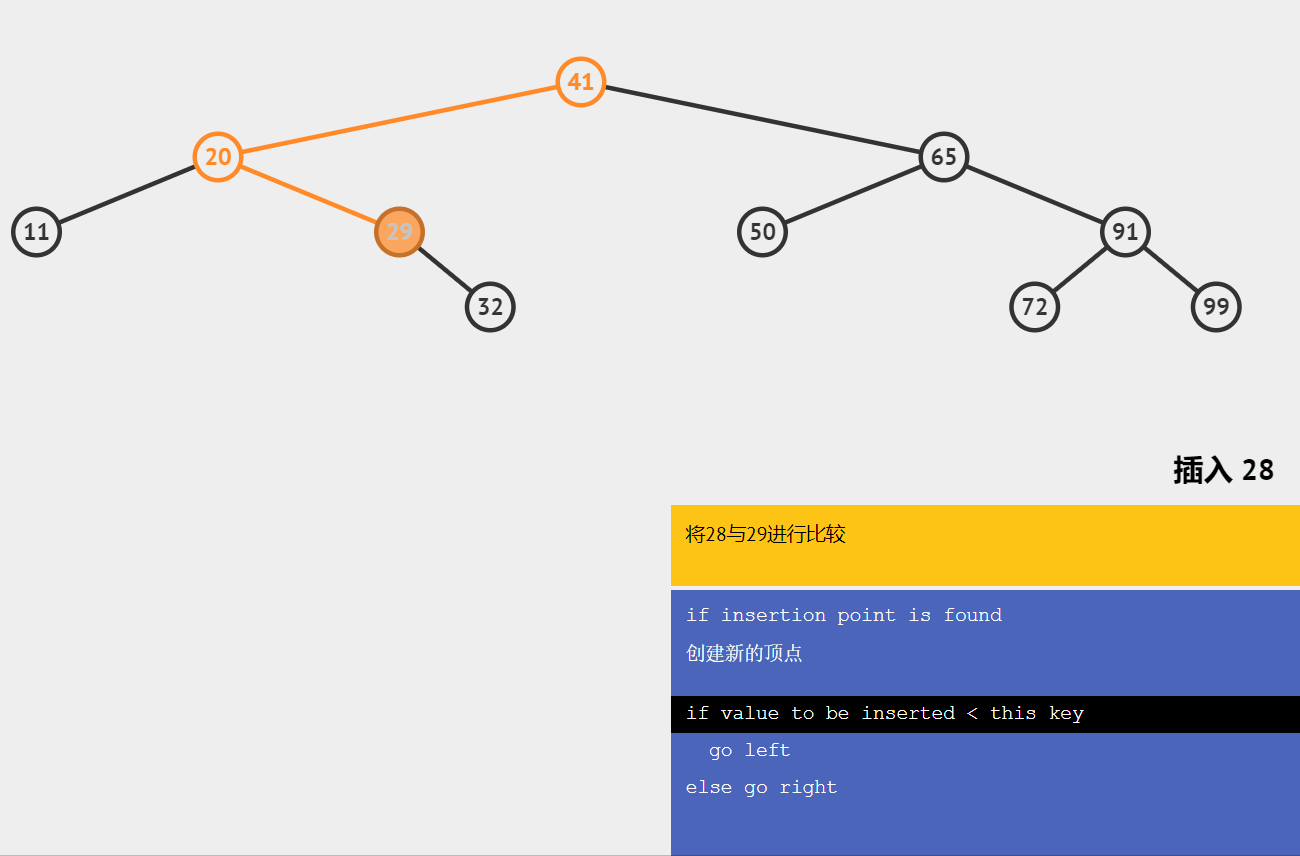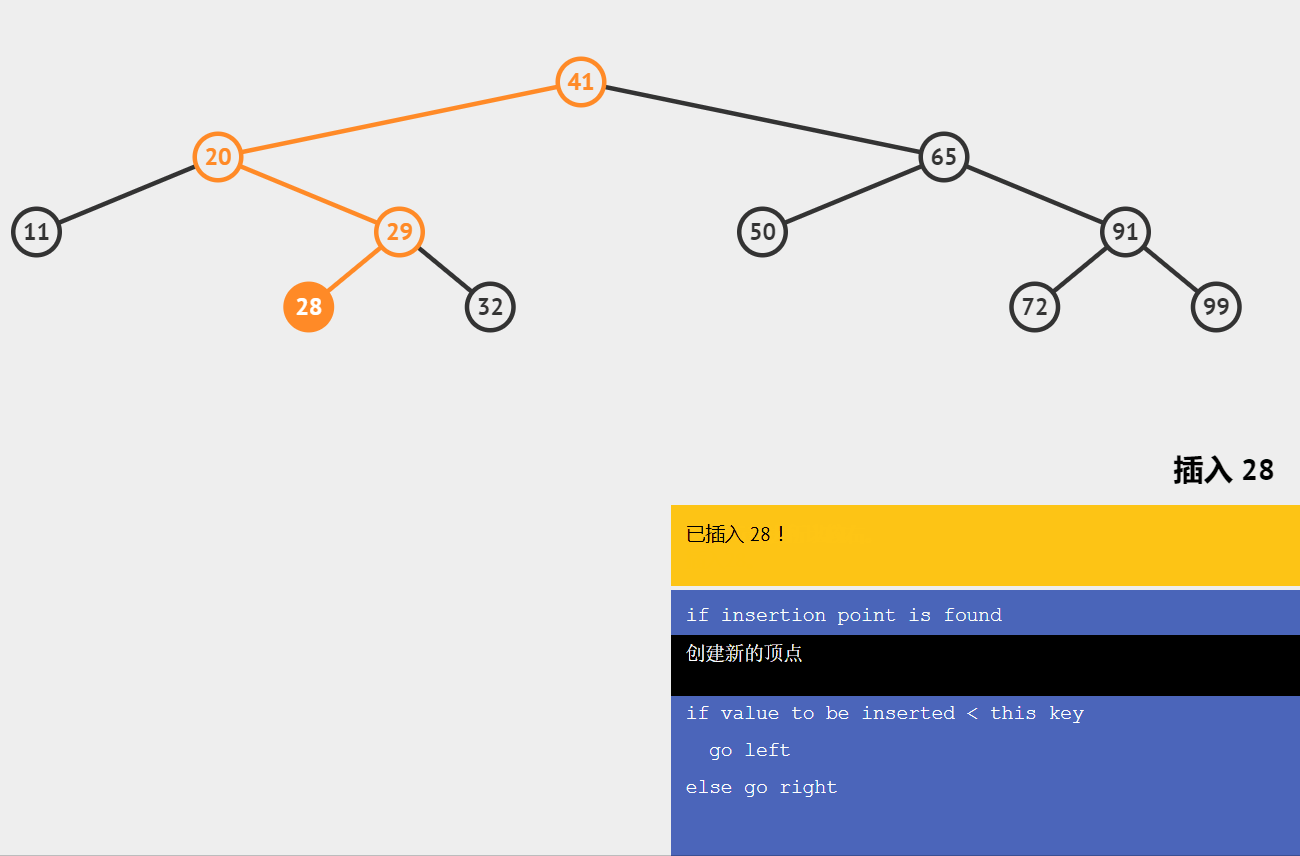
🍋插入节点
类似于查找,拿插入值与当前节点值比较
小于向左,大于向右
直到左子树或者右子树为空时插入数据。
🍅遍历节点
遍历树按照特定的顺序访问每个节点。分为:前序遍历,中序遍历,后序遍历。
二叉搜索树常用为:中序遍历。
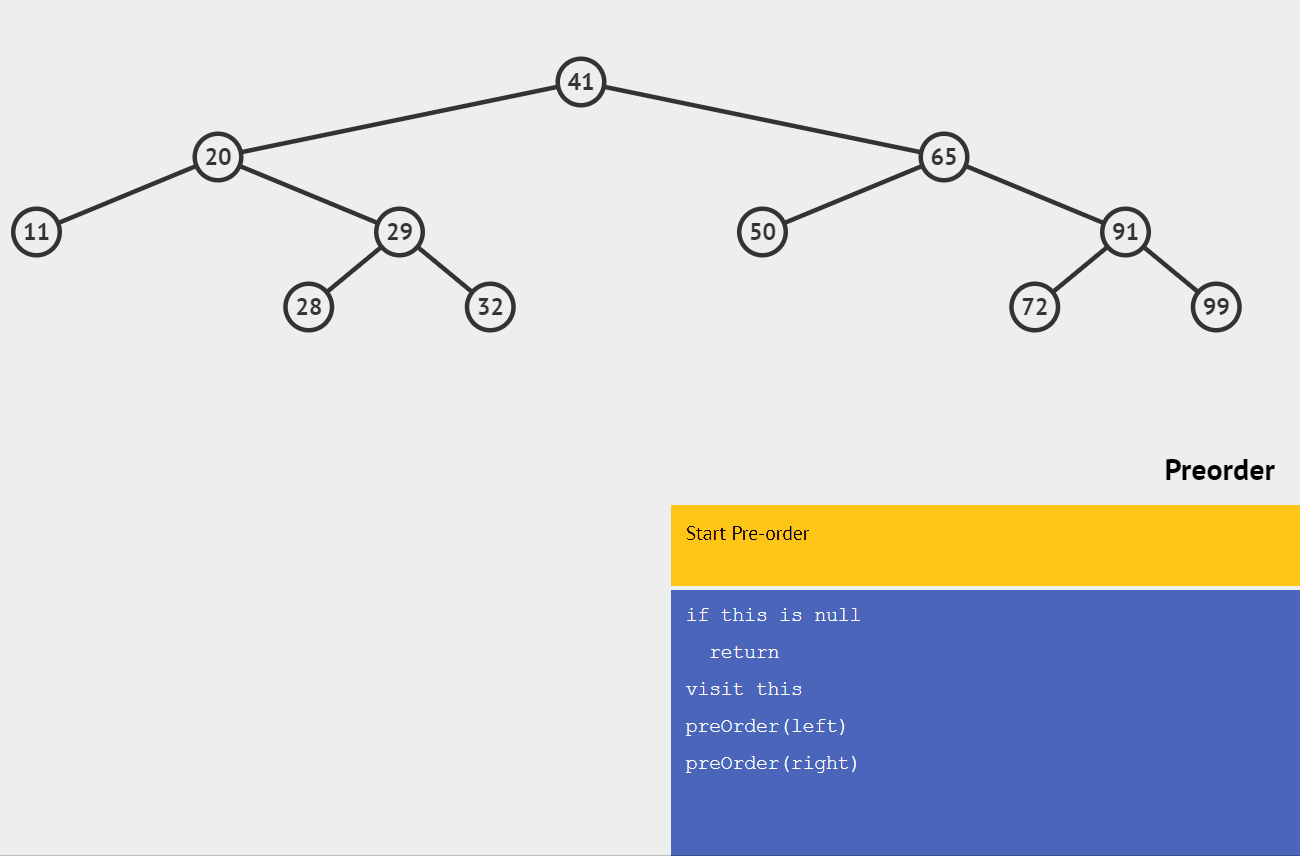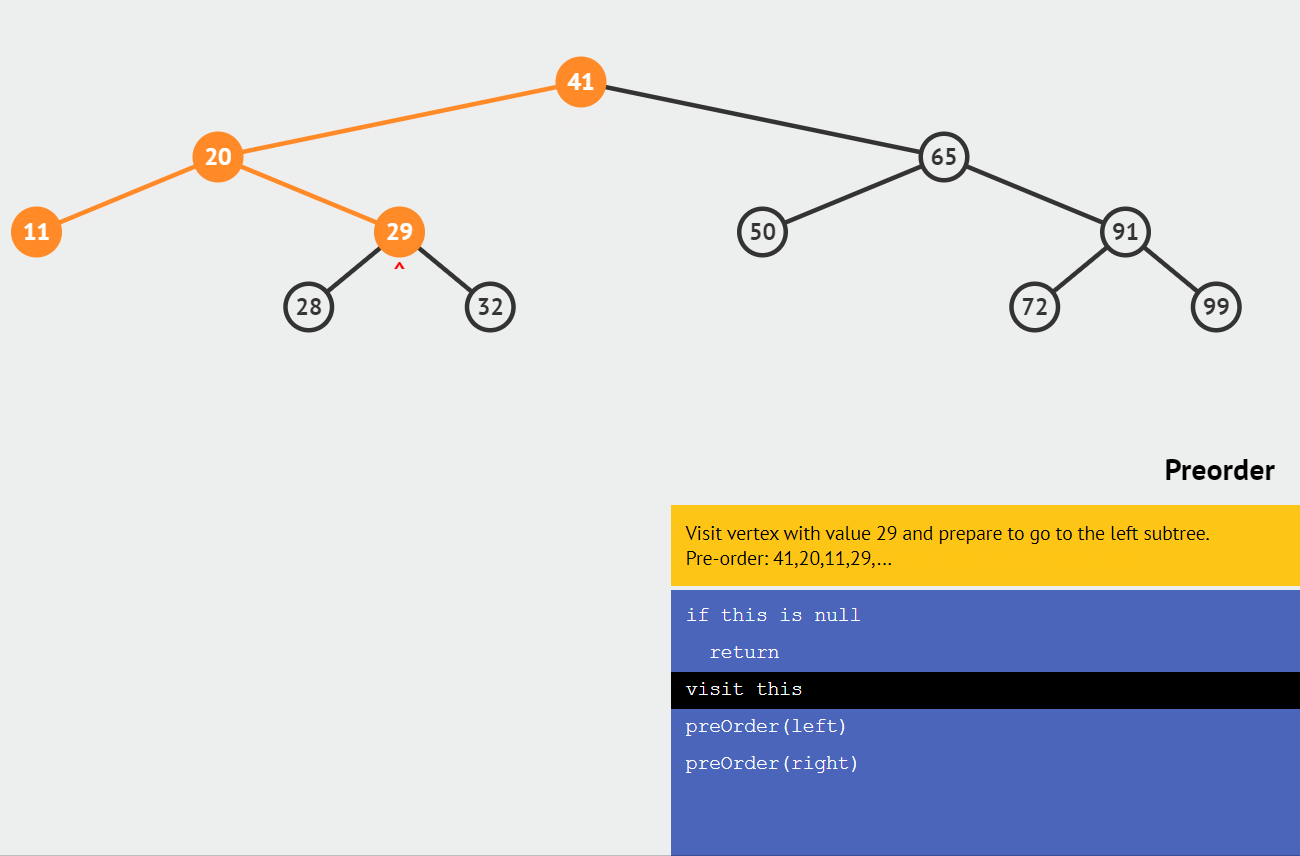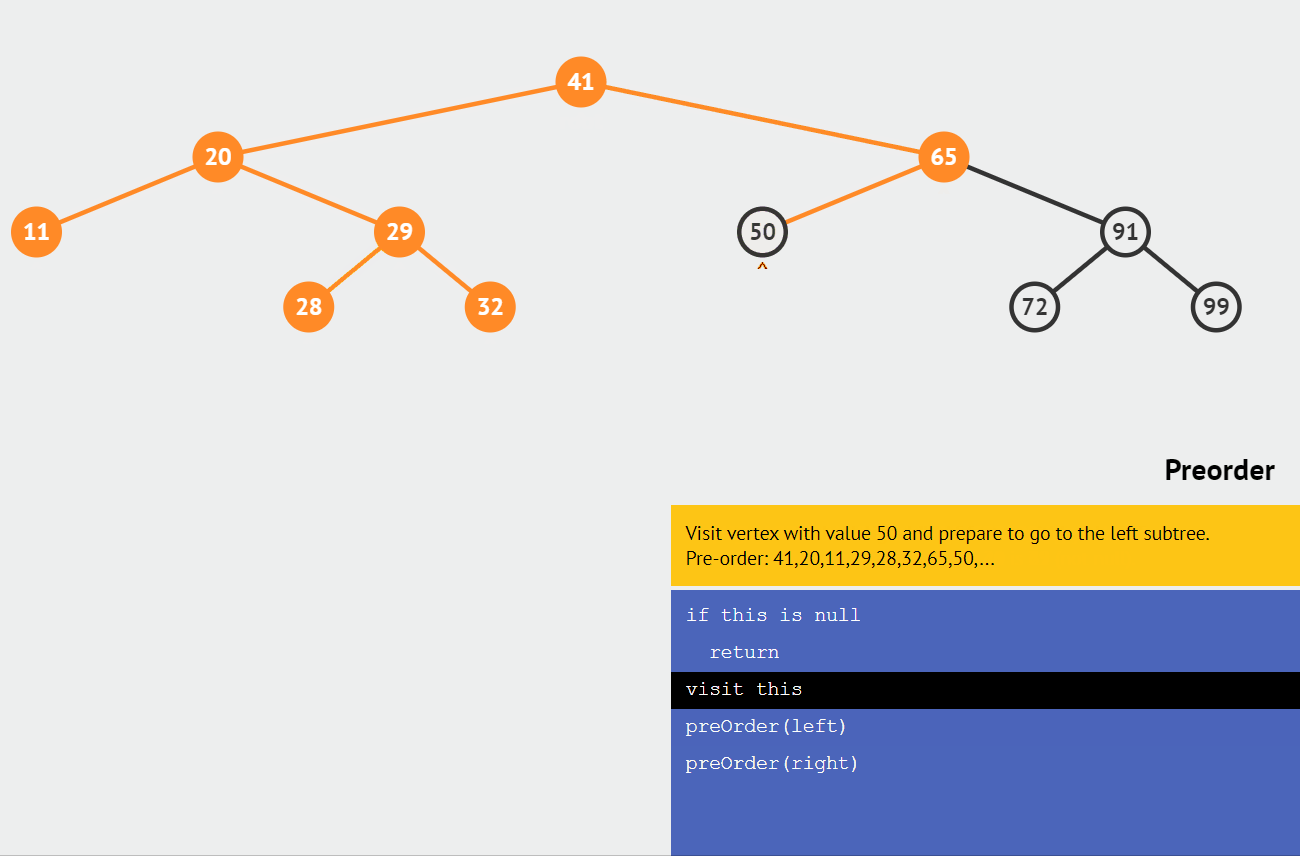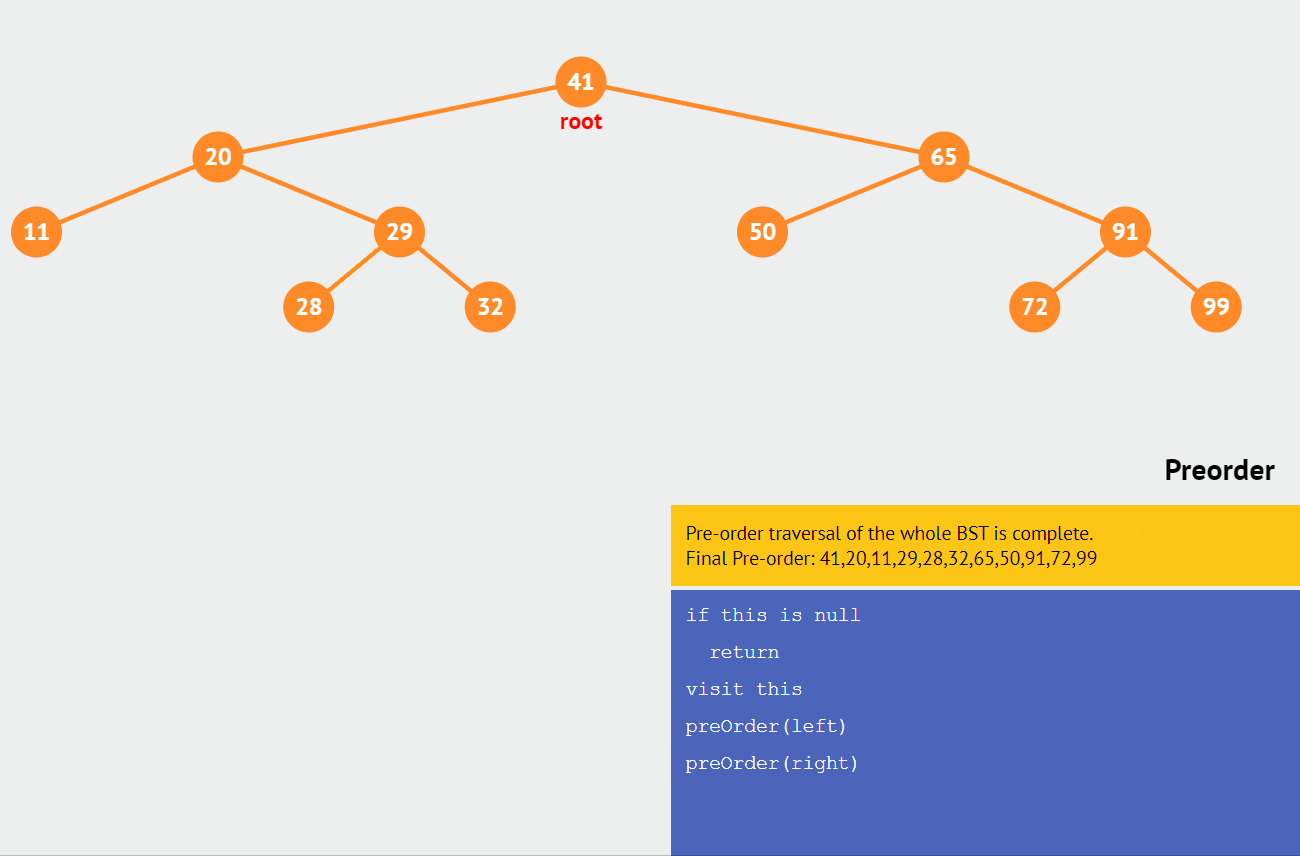
🍕 前序排序
如果二叉树为空,则空操作;否则依次执行以下操作。
- 访问根结点
- 先序遍历根结点的左子树
- 先序遍历根结点的右子树
结果为:41,20,11,29,28,32,65,50,91,72,99
🧀 后序排序
如果二叉树为空,则空操作;否则依次执行以下操作。
- 后序遍历根结点的左子树
- 后序遍历根结点的右子树
- 访问根节点
结果为:11,28,32,29,20,50,72.99.91,65,41
提示:目前网站不支持后序排序动画;
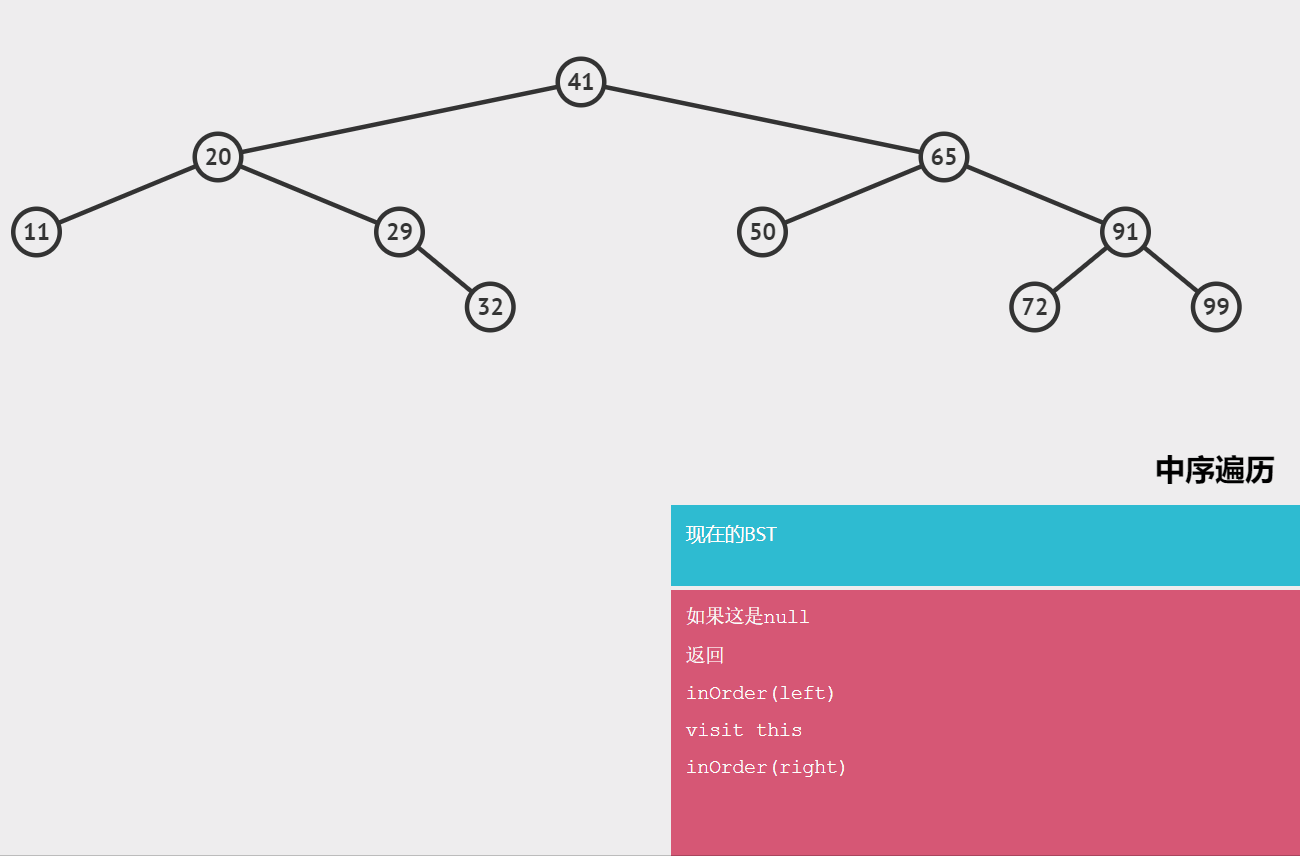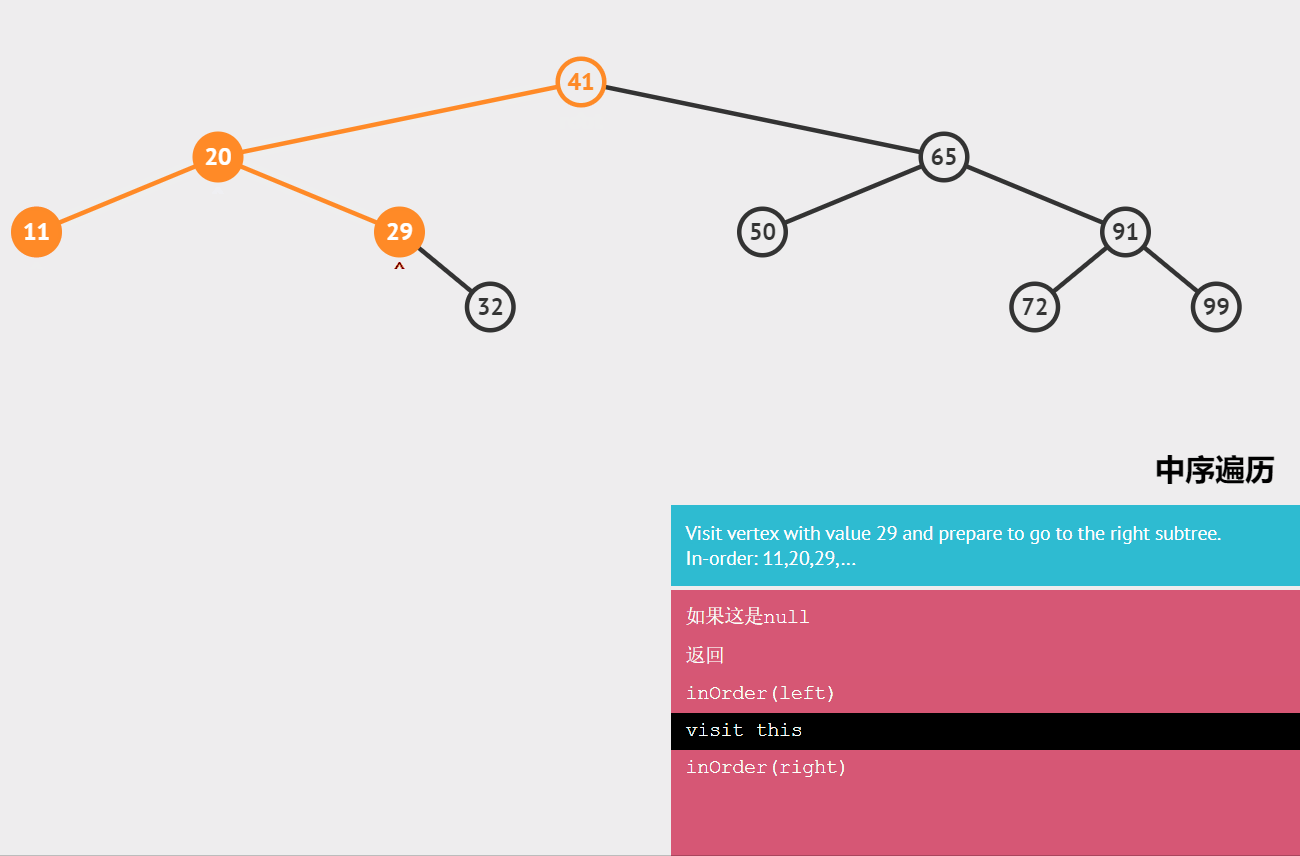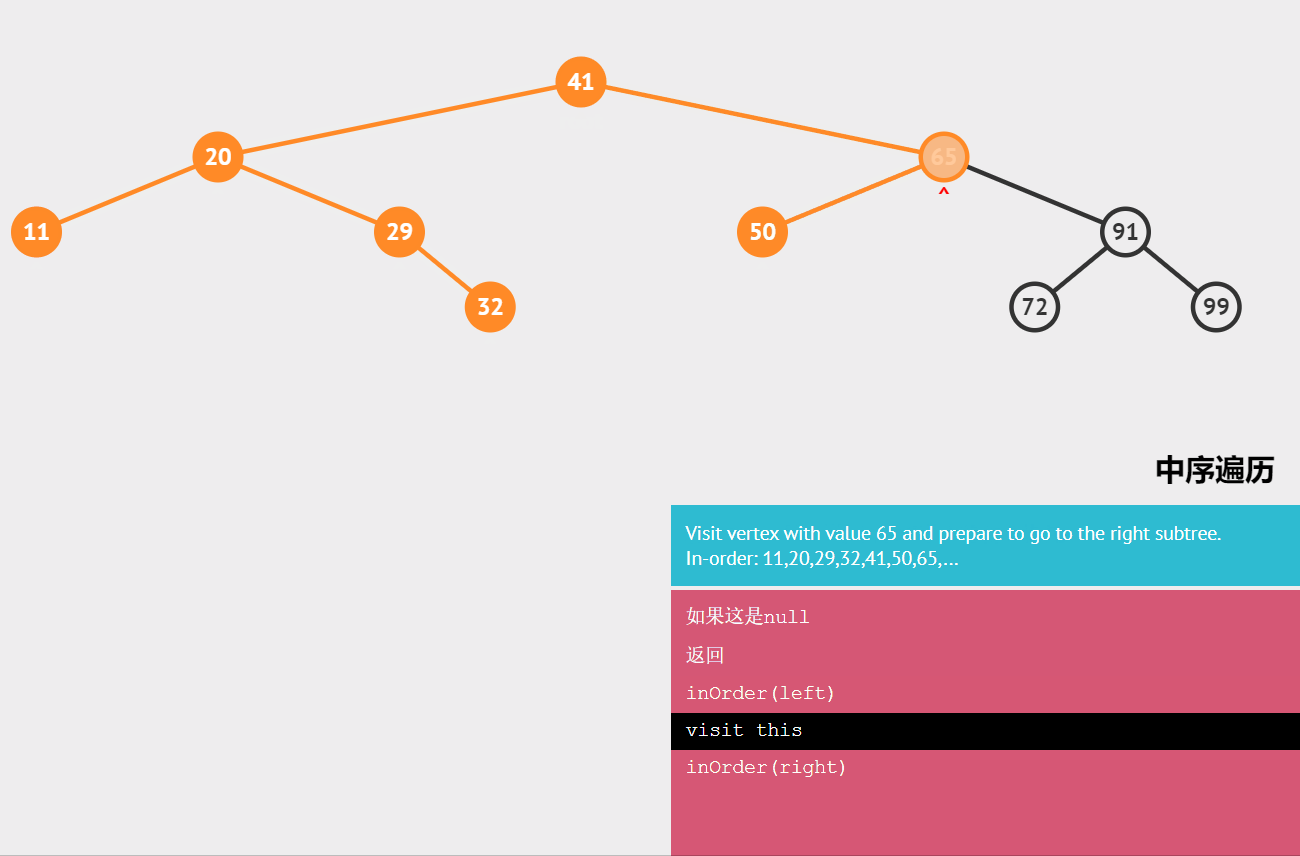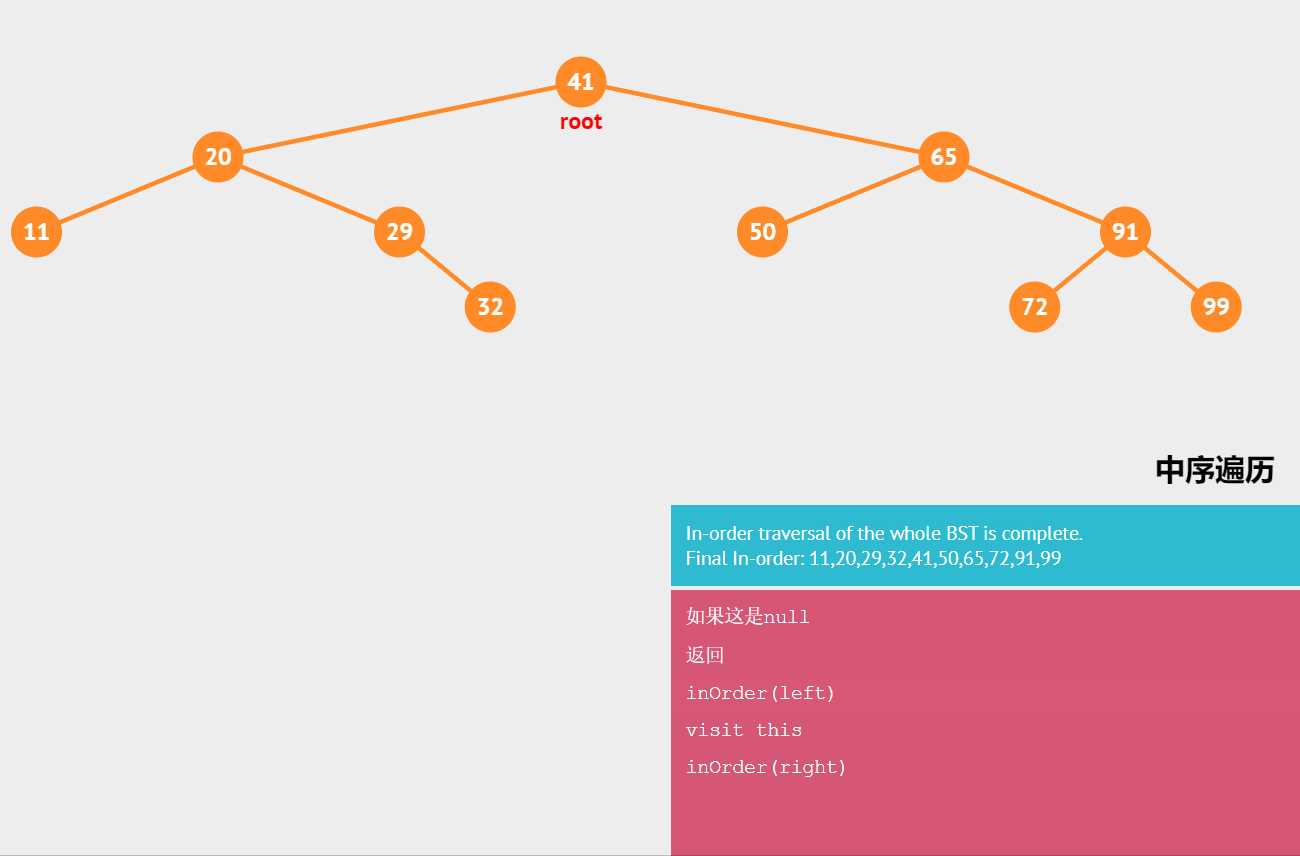
🍟 中序排序
如果二叉树为空,则空操作;否则依次执行以下操作。
- 中序遍历根结点的左子树
- 访问根结点
- 中序遍历根结点的右子树
结果为:11,20,29,32,41,50,65,72,91,99
🍇删除节点
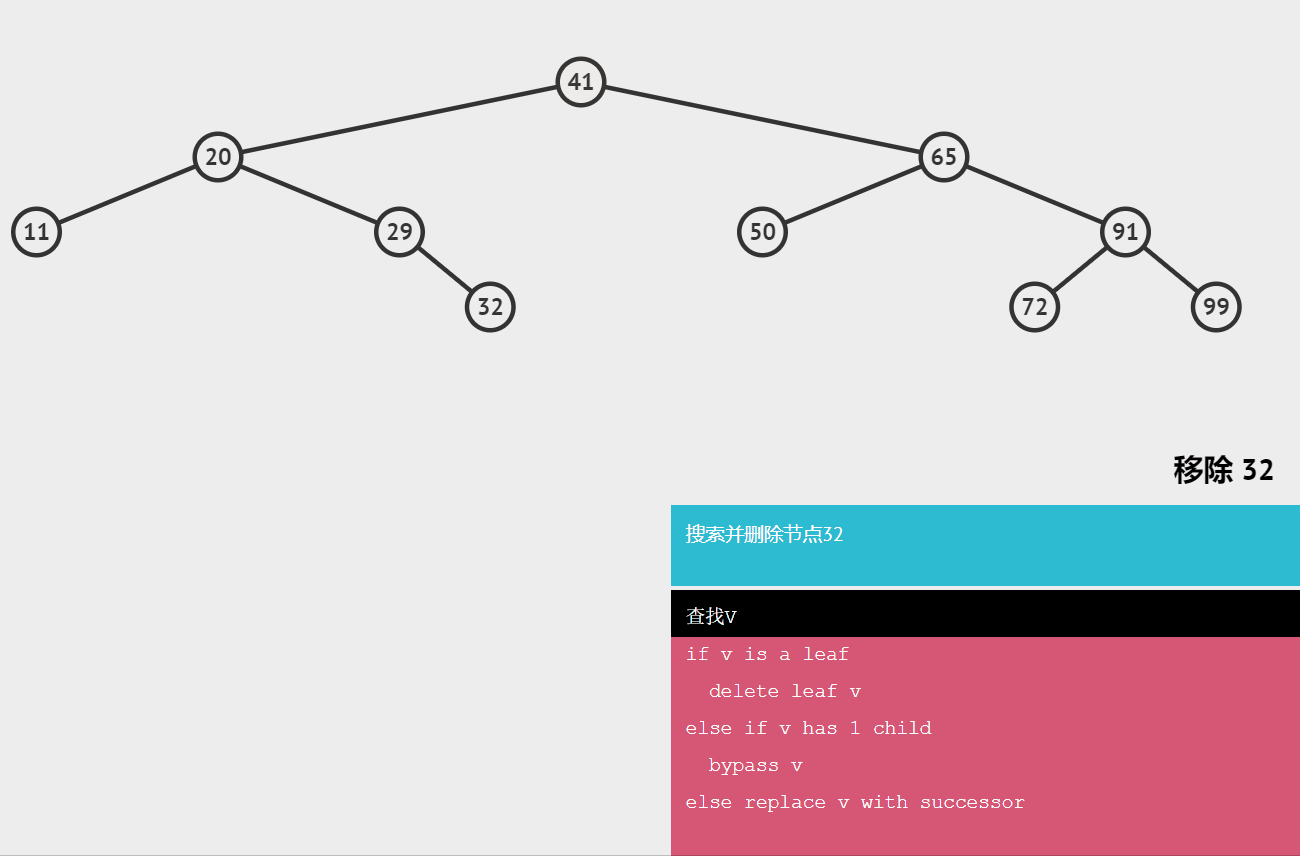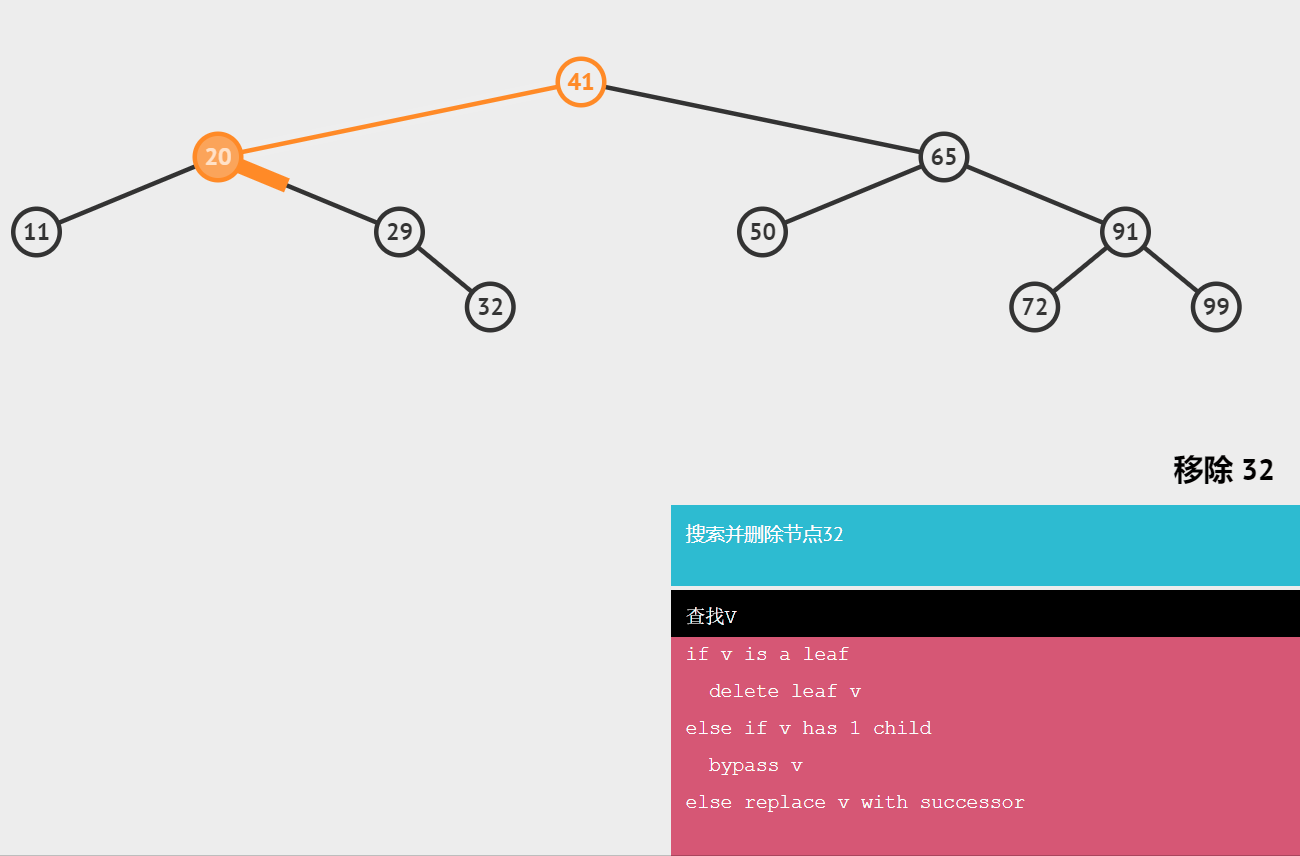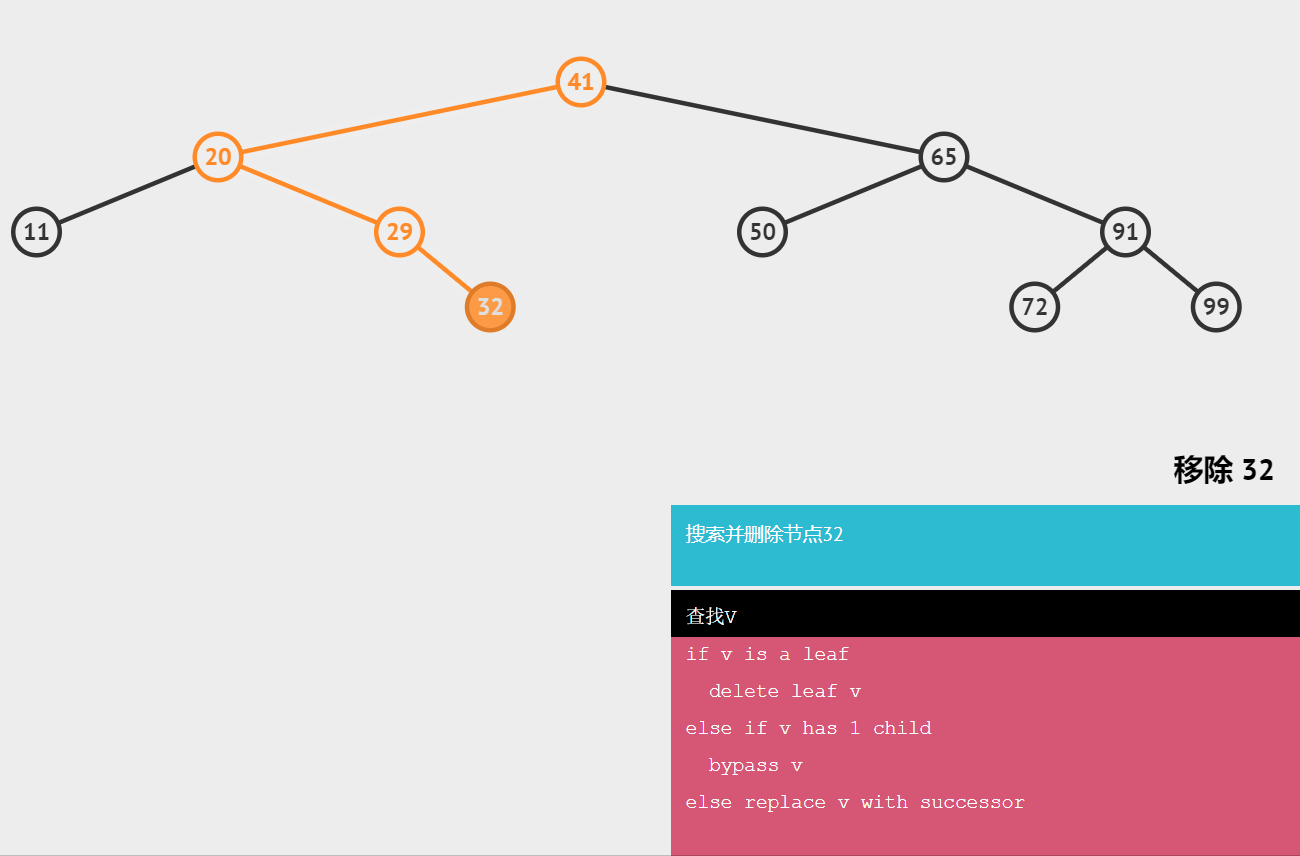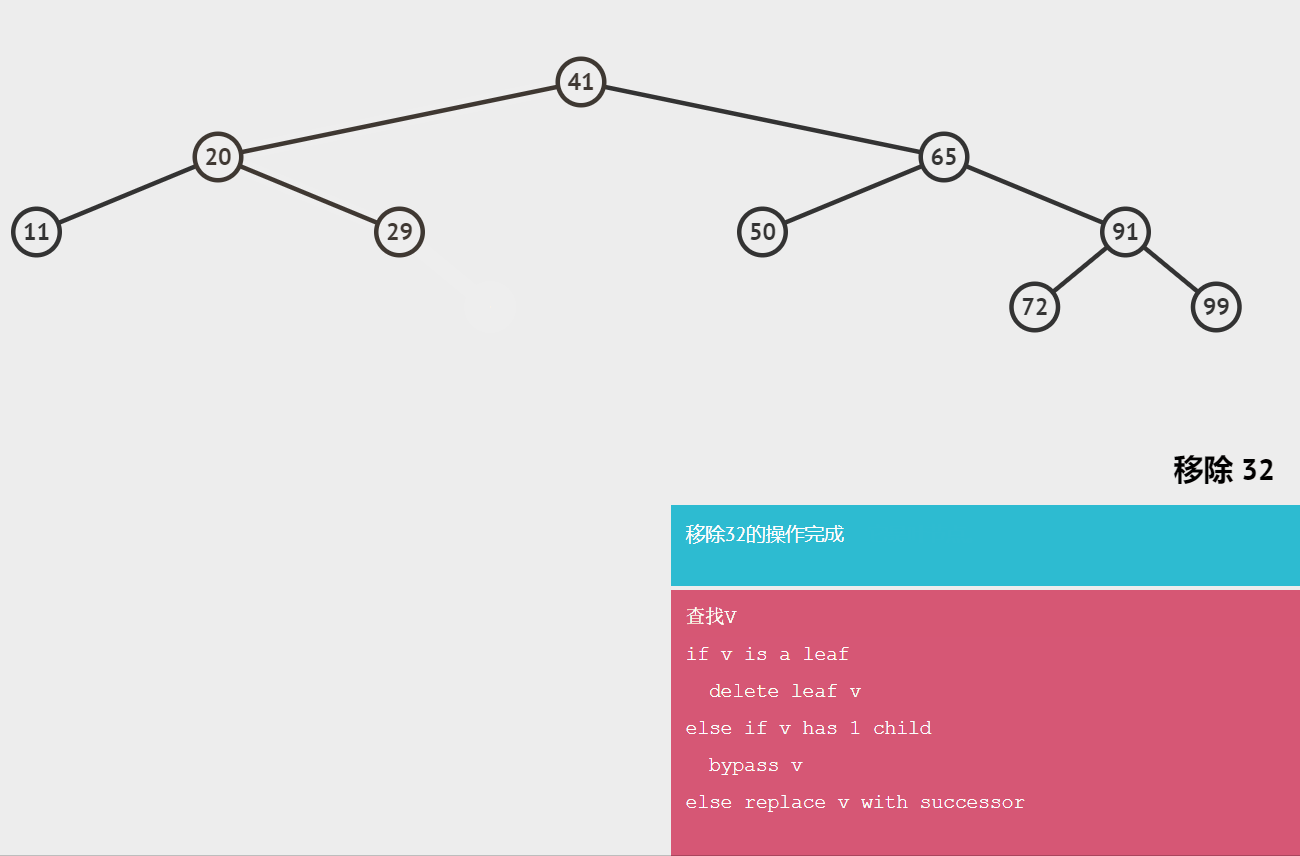
删除节点情况比较多
🍖删除无子节点的节点
只需要改变节点的父节点引用该节点的值,即:将其引用改为null.
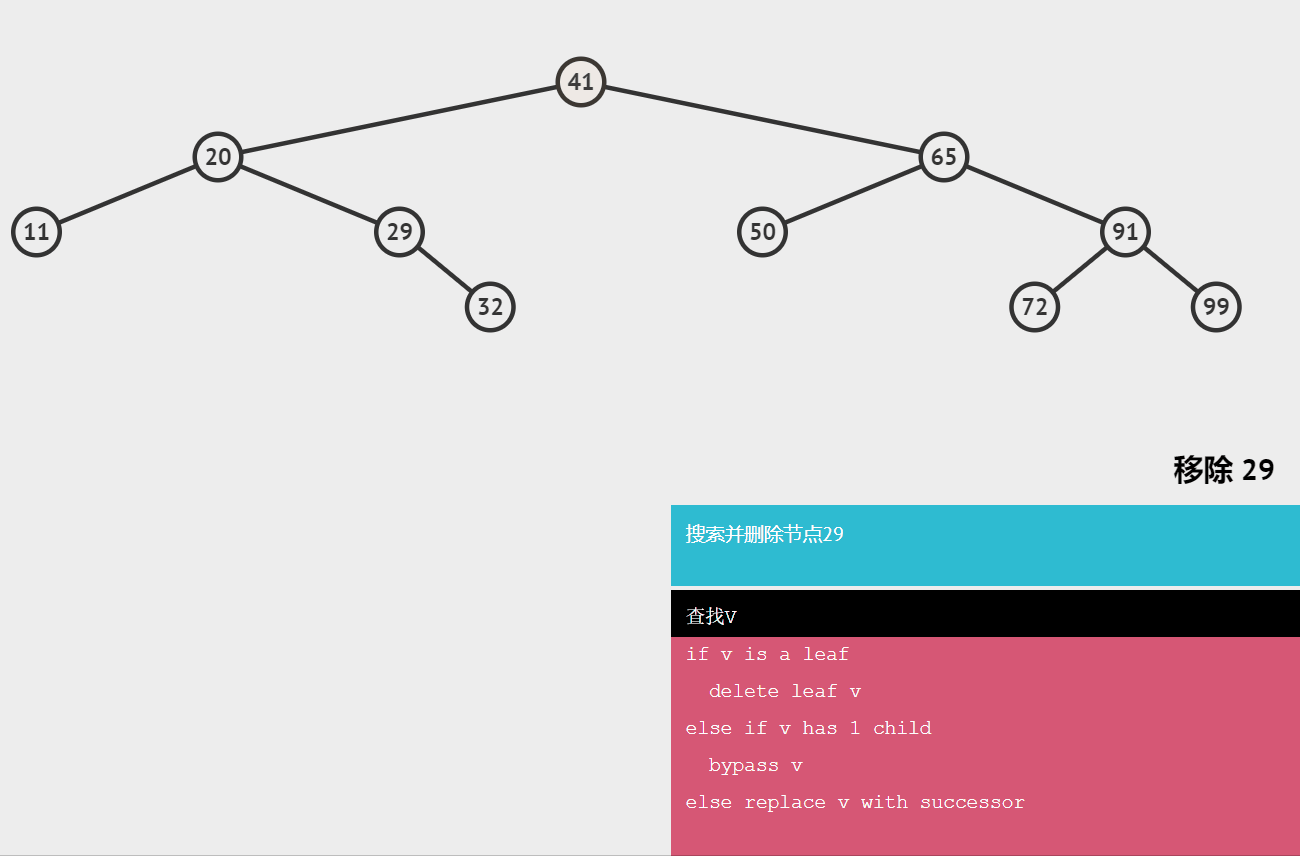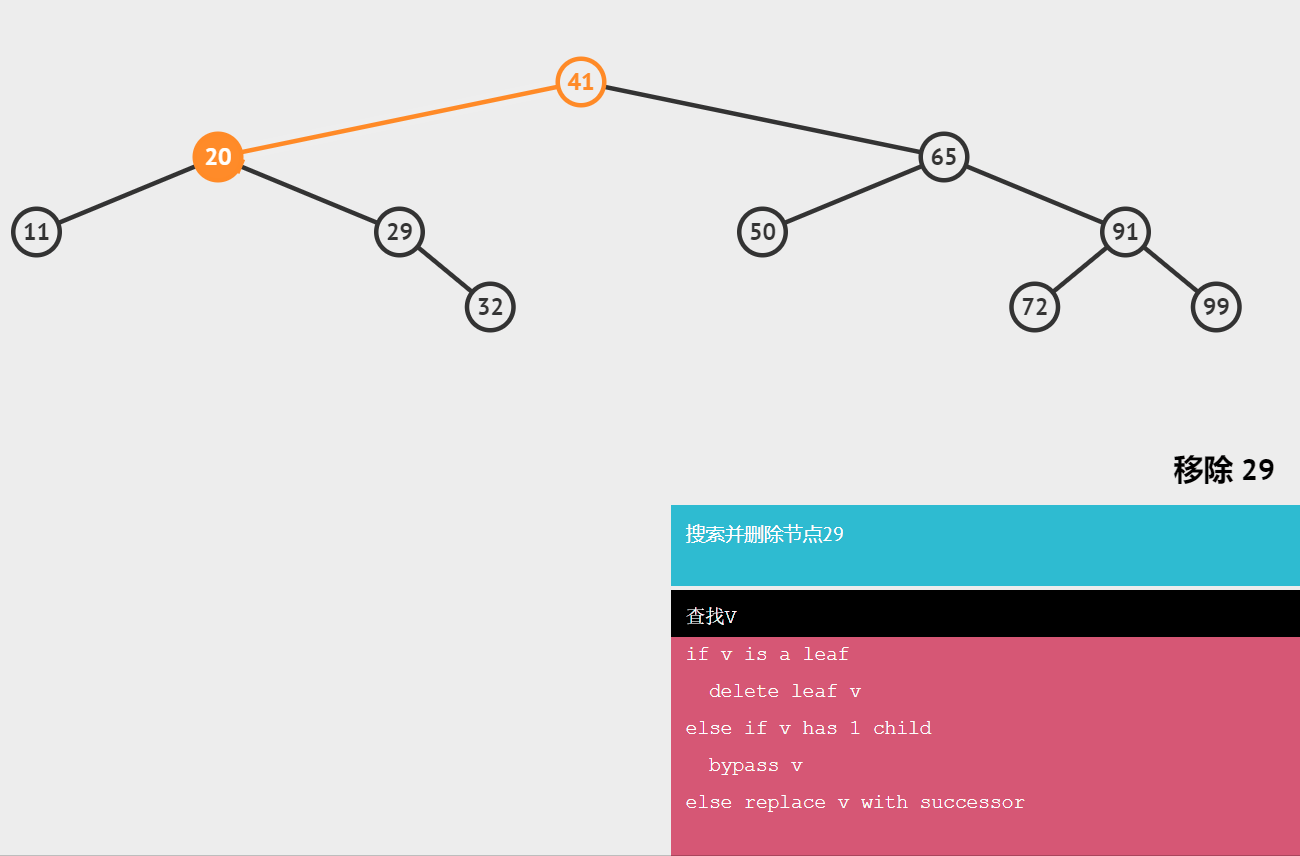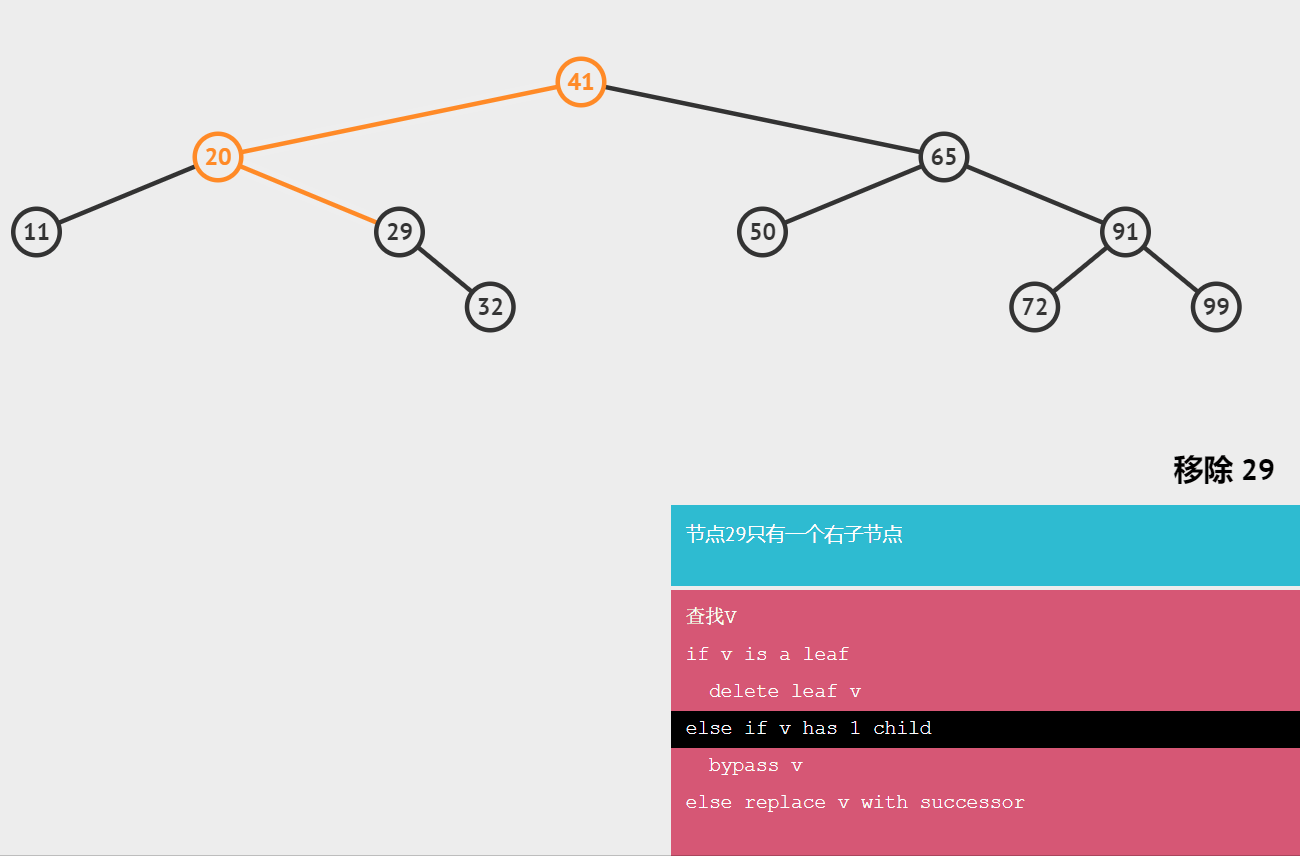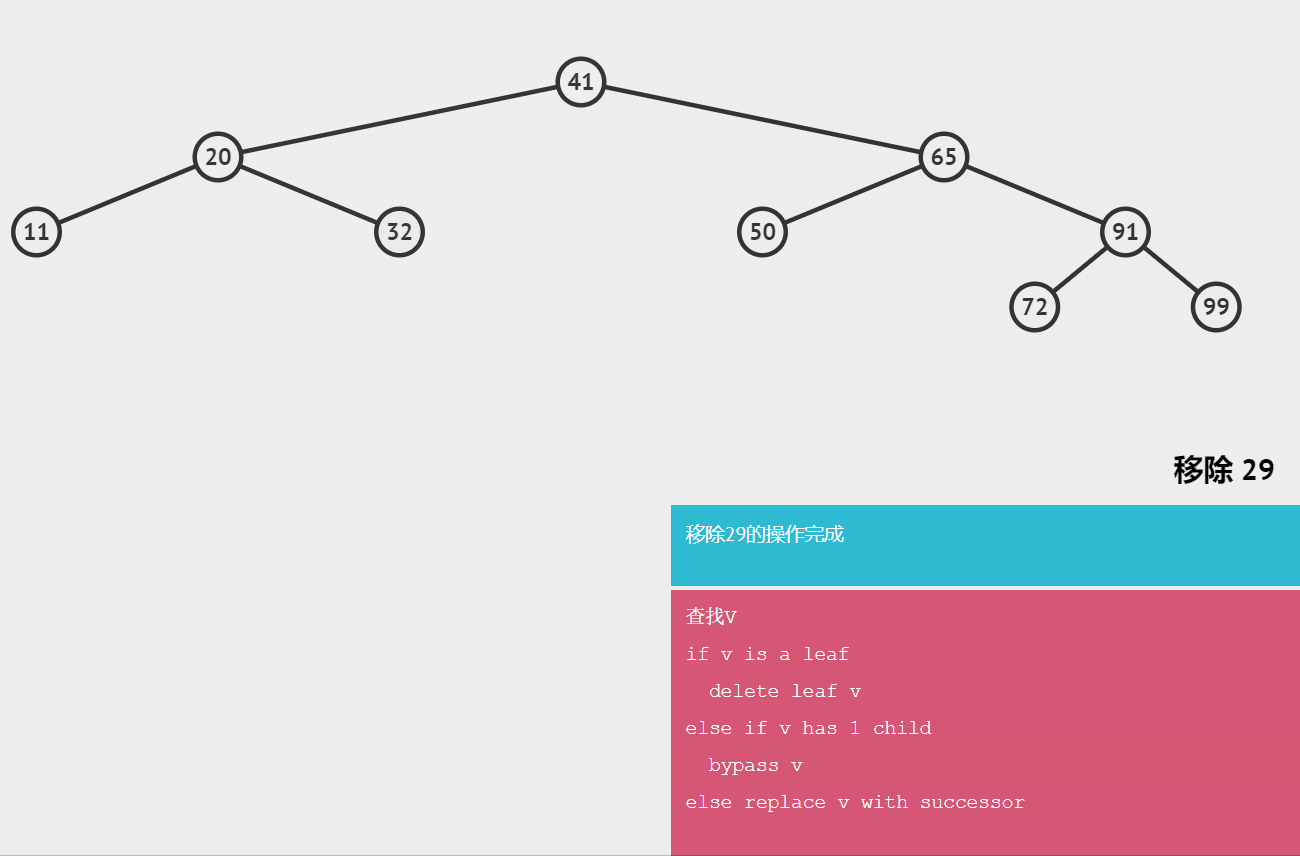
🌺删除有一个子节点的节点
需要将该节点的父节点指向该节点的引用指向该节点的子节点
🔥删除有两个子节点的节点
需要找删除节点的后继节点,用后继节点代替删除的节点;
后继节点:大于节点的最小节点。
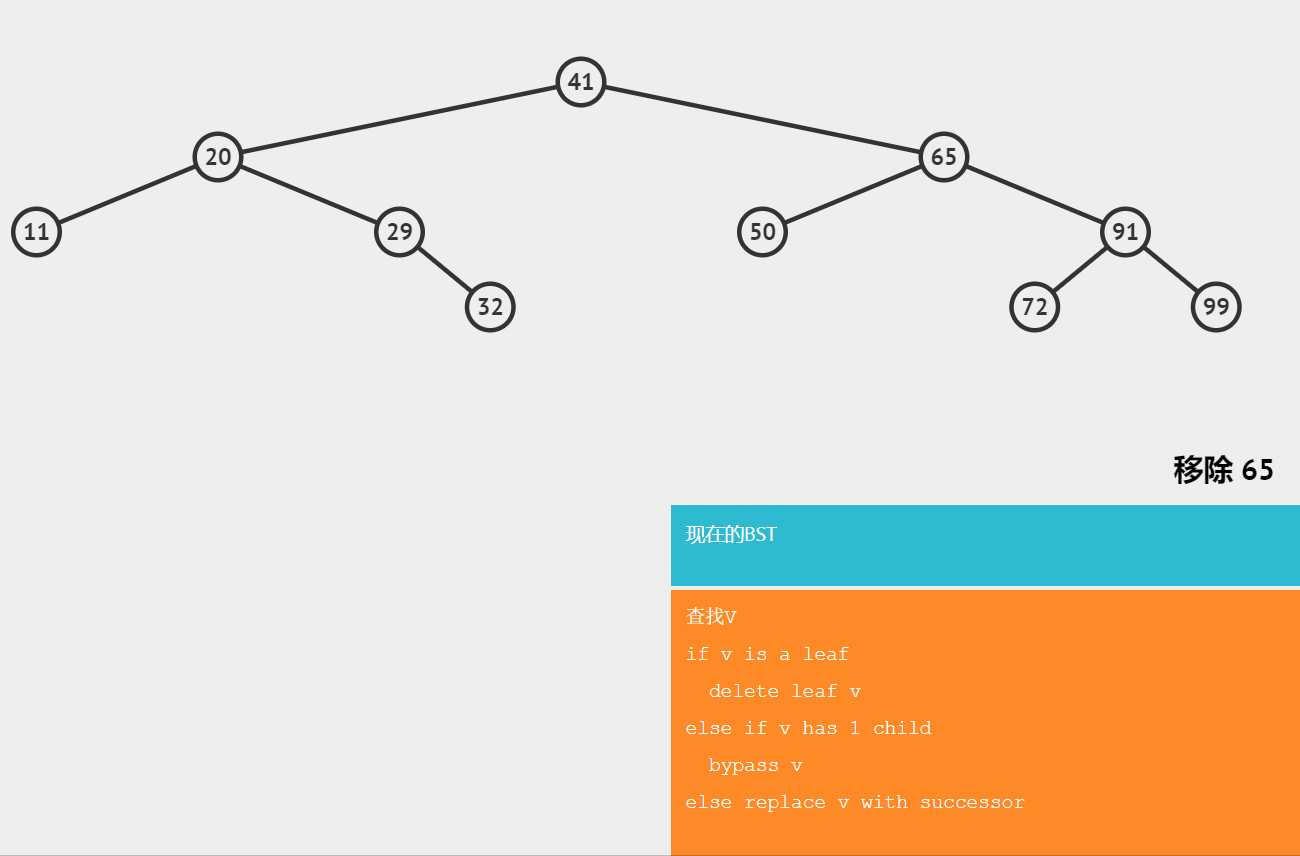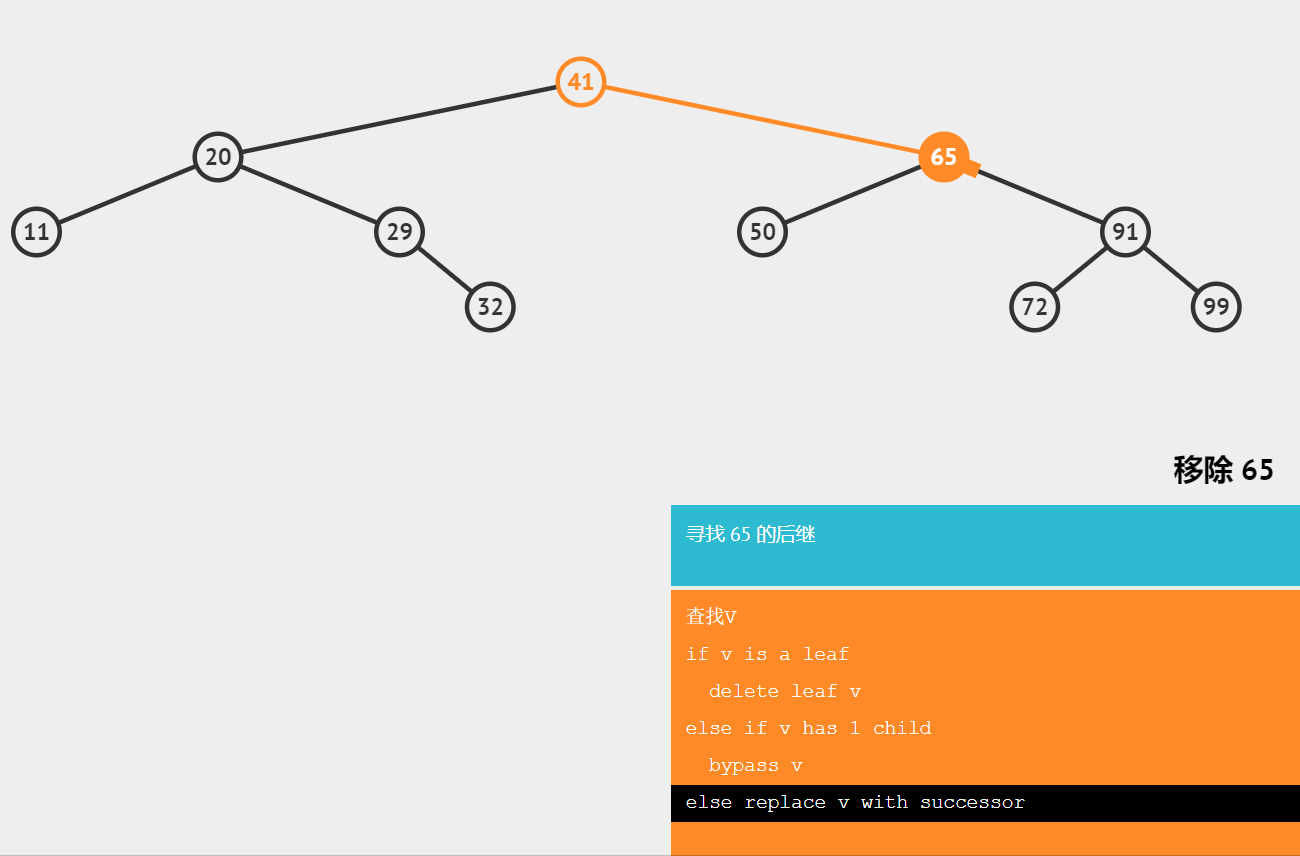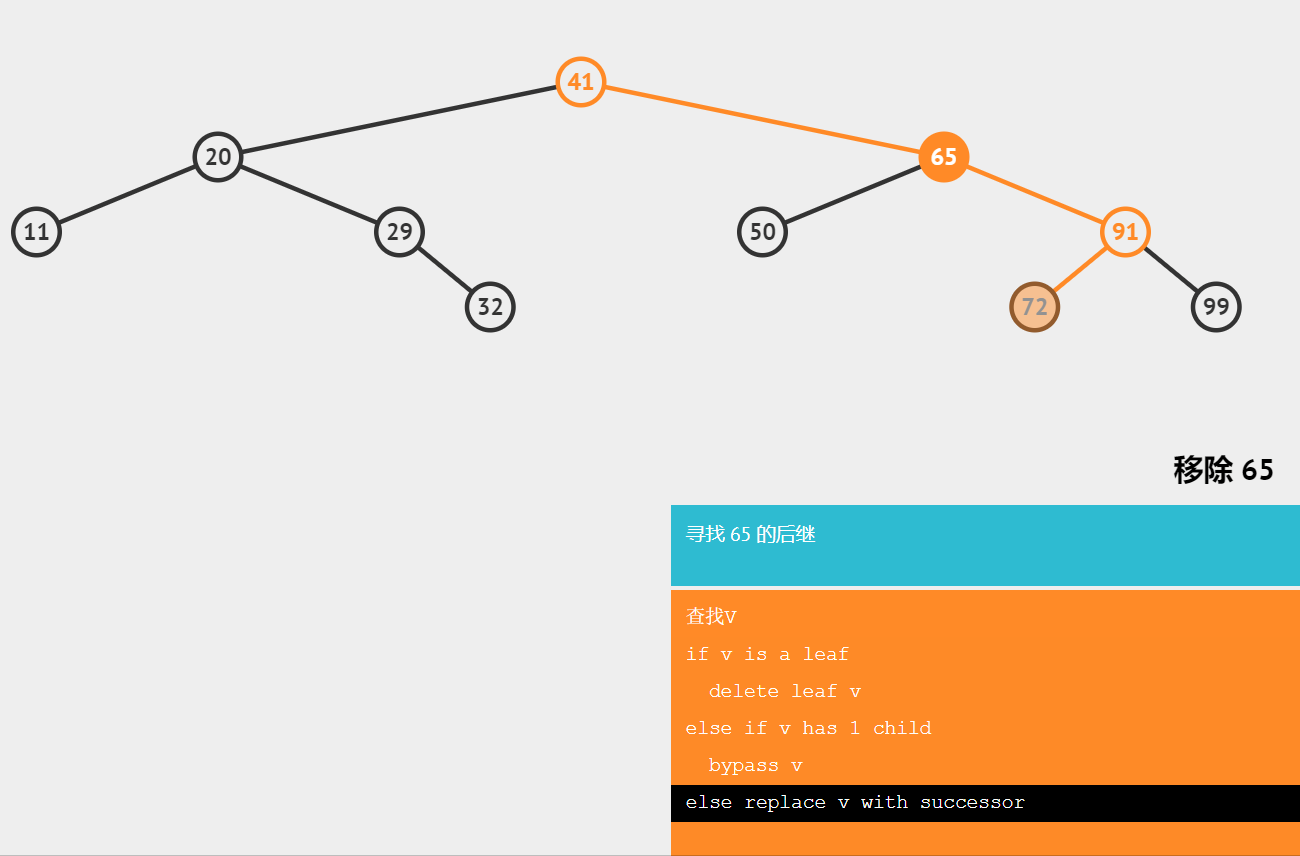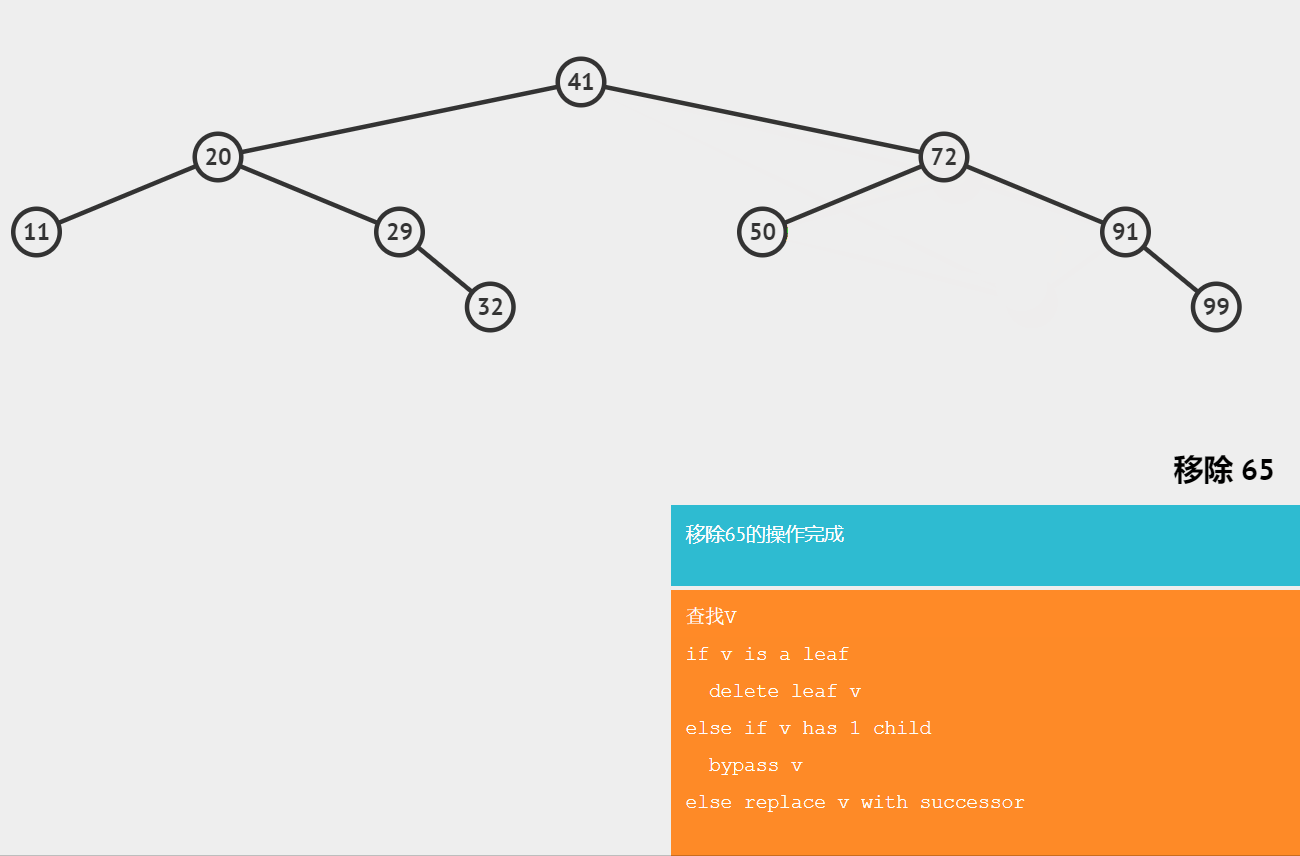
⭐️时间复杂度分析
🐈二分查找算法的
数组[1,2,3…100]
- 暴力算法:遍历数组查找性能不稳定,取决于查找元素位置。
- 二分查找算法:数据源必须是有序数组,性能优异,每次迭代排除数据的一半。
public static void main(String[] args) {int[] arr=new int[]{0,1,2,3,4,5,6,7,8,9,10};System.out.println(binarySerrch(arr,1));}public static int binarySerrch(int[] arr,int data){int begin=0;int end=arr.length-1;while (begin<=end){//起始位加上中间长度,获取中间位置下标int mid=begin+(end-begin)/2;System.out.println("中间位置-->"+mid);if (arr[mid]<data){begin=mid+1;}else if (arr[mid]==data){return mid;}else {end=mid-1;}}return -1;}
二分查找缺陷:强制依赖有序数组
数组缺陷:不能快速插入,不能灵活扩容
链表可以弥补数组缺陷
📜综上,二分查找如何才能既要高性能,又要链表一样灵活。可以使用二叉搜索树来使用。
二分查找时间复杂度为:
N/(2 ^ K)=1 => (2 ^ K)=N => K=log2(N) => O(logN)
🎉缺陷
这样的二叉树就退化为了链表。 此时时间复杂度为:O(N)

⭐️平衡二叉树(AVL树)
- 具有二叉树全部特征。
- 每个节点的左子树和右子树高度差至多等于1

由于第二条规则,在每次插入,删除时,几乎都会破坏这个规则。在调整树的过程,大大影响性能。引入红黑树。
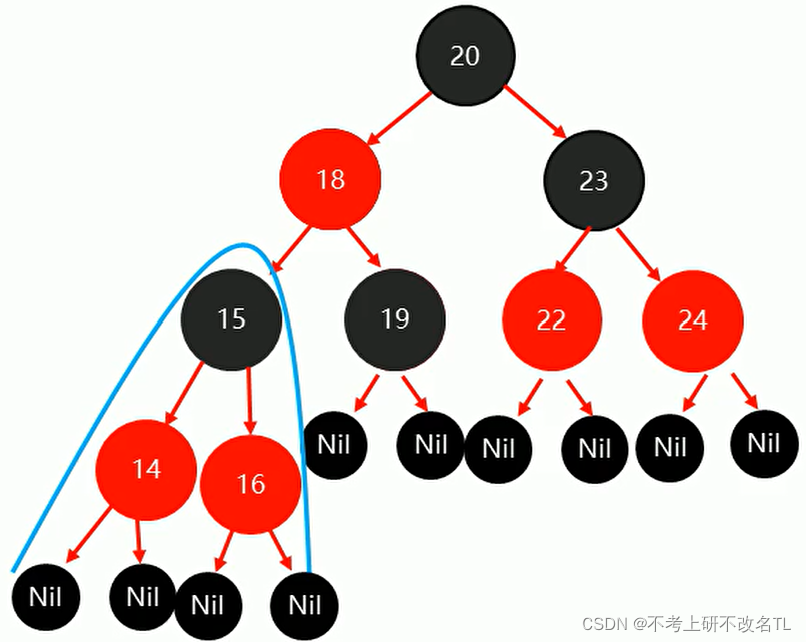
🔥 红黑树
🔎红黑树定义:全称是Red-Black Tree,又称为“红黑树”,它一种特殊的二叉查找树。红黑树的每个节点上都有存储位表示节点的颜色,可以是红(Red)或黑(Black)。
红黑树的特性:
(1)每个节点或者是黑色,或者是红色。
(2)根节点是黑色。
(3)每个叶子节点(NIL)是黑色。 [注意:这里叶子节点,是指为空(NIL或NULL)的叶子节点!]
(4)如果一个节点是红色的,则它的子节点必须是黑色的,不能有两个红色节点相连。
(5)从一个节点到该节点的子孙节点的所有路径上包含相同数目的黑节点。(黑高,黑色完美平衡)

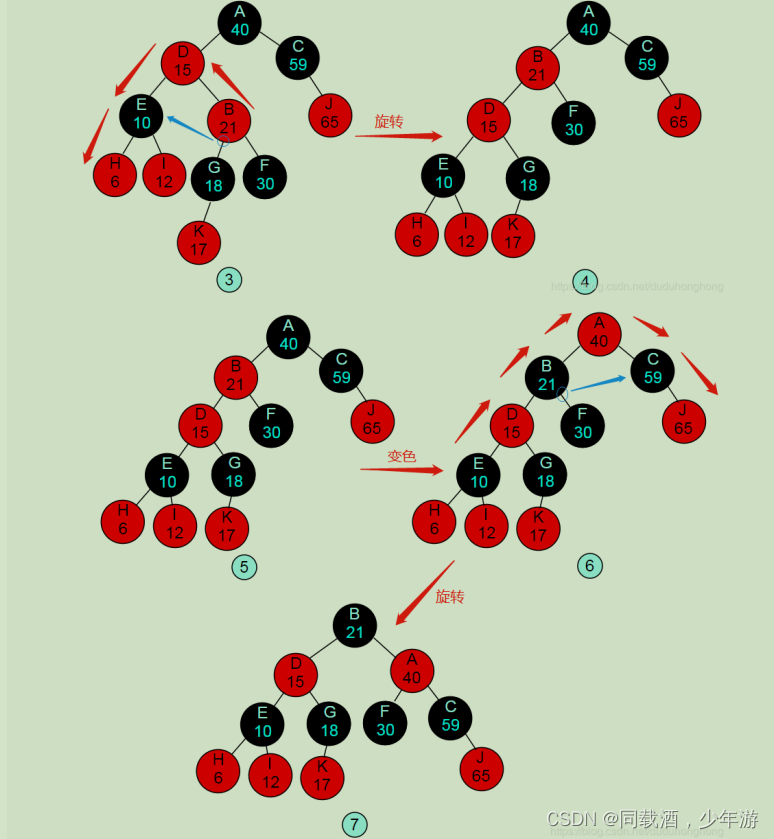
红黑树能自平衡:变色,左旋,右旋。
旋转和颜色变换规则:所有插入的点默认为红色
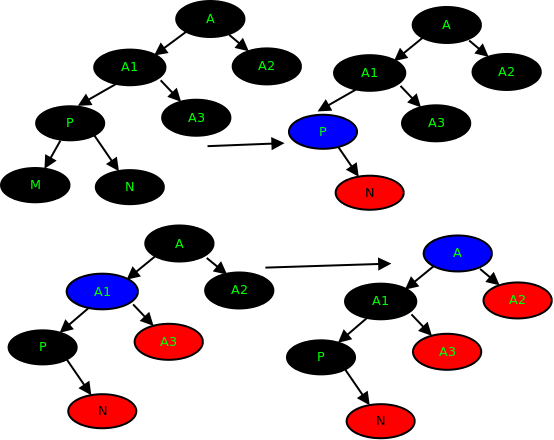
✌变色
当前结点的父亲是红色,且叔叔结点也是红色:
(1)把父节点设为黑色
(2)把叔叔也设为黑色
(3)把祖父也就是父亲的父亲设为红色(爷爷)
(4)把指针定义到祖父结点设为当前要操作的(爷爷)分析的点变换的规则
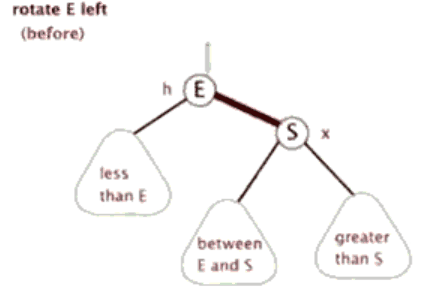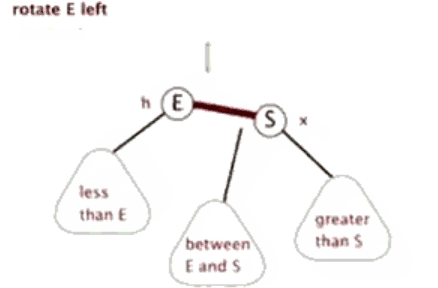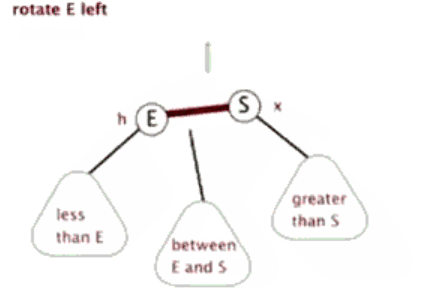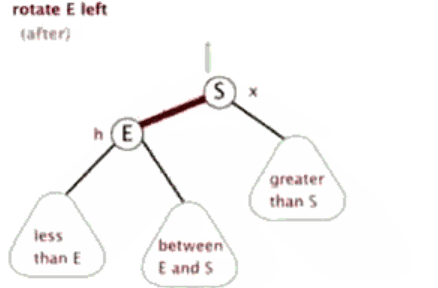
🎄左旋
当前父结点是红色,叔叔是黑色的时候,且当前的结点是右子树。左旋以父节点作为左旋
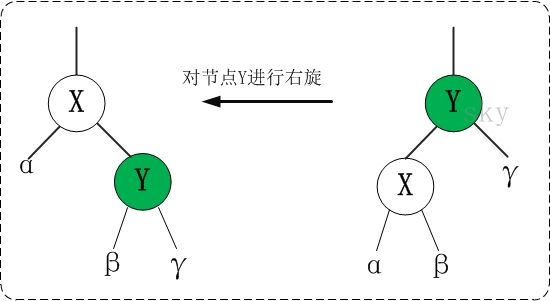
🎄右旋
当前父结点是红色,叔叔是黑色的时候,且当前的结点是左子树。右旋
(1)把父节点变为黑色
(2)把祖父结点变为红色(爷爷)
(3)把祖父结点旋转(爷爷)
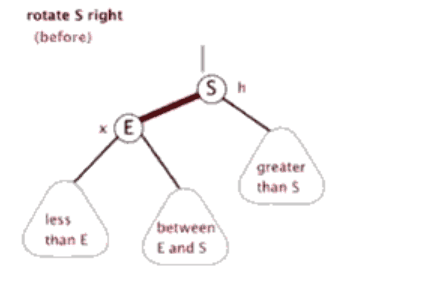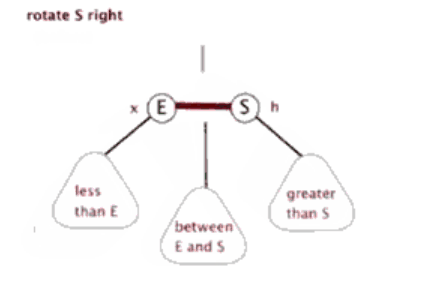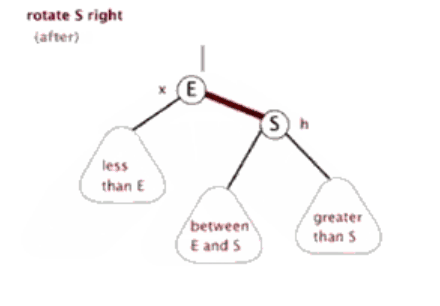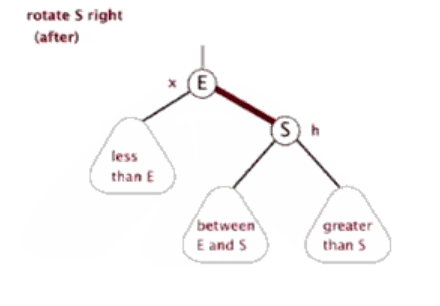
所以,我们发现左旋和右旋是一个相对的操作。
关于红黑树旋转的代码,其实很简单,我大概说一下如何实现,其实每个节点有这么几个属性:
1、父节点的指向
2、子节点的指向(有两个,一个左子节点,一个右子节点)
3、该节点的颜色
4、该节点存储的value(当然如果是map,那就是该节点的key和value都要存,然后按照key的大小来插入新节点)
所以当我们做旋转的时候,只需要把该节点的父节点指向该节点的子节点,然后把子节点的一条腿接到该节点上。
————————————————
版权声明:本文为CSDN博主「lsr40」的原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接及本声明。
原文链接:https://blog.csdn.net/lsr40/article/details/85245027
🔎参考博客
红黑树插入数据(变色,左旋、右旋)
数据结构:树(Tree)【详解】