红黑树结构原理的图文讲解（非代码）

article/2025/10/1 6:13:07

1.引言

HashMap的基本结构是数组，链表和红黑树。以数组为基本形态，数组中的元素先以链表形式储存，当链表的长度超过8时（包含数组上的那个链表头）就会将链表转换为红黑树，以加快修改和查询效率。当然除了HashMap还有很多地方都会用到红黑树，理解红黑树的原理还是比较重要的。

2.概念与由来

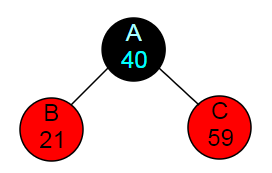
红黑树的本质是二叉树，二叉树在插入元素的时候是根据关键字（可以理解为用来识别每个节点的id，一般是hash来判断）的大小来判断插入到哪一个分支的，如下图所示：

（备注：大写字母代表每个节点相当于每个节点的名字没有实际意义在本文中方便文字说明，数字代表每个节点的关键字的大小有实际意义）

规律是父节点的关键字大于左子节点且小于右子节点，即B<A<C的关系。

举个插入的例子：当新插入一个元素是会判断其关键字大小如果大于A的，则插入到A的右子节点也就是C，但是此处已经有了节点存在了，然后继续判断是否大于C，如果小于C，则插入到C的左子节点，正好此处为空存在，插入后形成下图所示：

但是按照这个规则插入就遇到一个问题，如下图所示的情况：

这样的现状导致查询效率非常低，如果要找节点J，这样一串遍历下来就跟链表结构区别不大了，从而失去了树结构的优势。为了解决这个问题出现了平衡二叉树。而平衡二叉树在原始二叉树基础上加了平衡节点的机制，每插入一次元素后都会自动去判断是否失衡了，如果失衡了则会自动调整节点的布局结构使其从根节点（最顶端的节点）到每一个叶节点（最低端的节点）的距离不会相差太多。然而平衡二叉树的要求过于严格，几乎每一次插入都要调整节点的布局，使得插入操作效率变得很低，于是有了一个这种的办法那就是红黑树。

3.红黑树规则

一共如下四条规则：

每个节点不是红色就是黑色的；
根节点（顶端节点）总是黑色的；
如果节点是红色的，则它的子节点必须是黑色的（反之不一定）；
从根节点到叶节点或空子节点的每条路径，必须包含相同数目的黑色节点（即相同的黑色高度）。

根据该规则，新插入的节点全都是红色，然后再根据具体情况做颜色变换甚至旋转。

原因：如果我们新插入的颜色是黑色的话，那么每插入一个节点都会违背第四条规则，这样就导致每次都做变色甚至旋转。当插入红色节点时，首先不会违反第四条规则，并且如果其父节点是黑色时也不会违反第三条，至于第二条规则大部分情况不会违背基本不予以考虑了。这样一来插入红色就不是每次都需要变色或者旋转了，这样就可以优化计算机的处理过程。

4.旋转机制

旋转分为向右旋转和向左旋转，下图所示是向右旋转，第一次看旋转的图可能会有些困难，但是看多了一眼就能看出来如何去旋转才能达到平衡了。外圈节点顺时针旋转一个节点的角度，中间红圈的连接点转移到C的位置（旋转完了C的位置就不是C了，这个箭头指示表示位置，而不是连接到哪一个节点）。

这样旋转完了就会变成下图所示的形状，这样就看上去平衡多了。整个旋转过程可以空间想象一下。

下图是向左旋转的示意图，这一个稍微复杂一点：

旋转完成后，如下图所示：

其实不管怎么旋转，宗旨就是两点，一是节点的高度（从顶点到低端的节点数量）差距不大，二是满足关键字大小的规则。

虽然刚开始看这种结构旋转有些不适应，看多了一看原始图就能想象出如何旋转可以达到平衡了。但是这只是从目的出发去使其平衡，光靠这些不能细化什么样的二叉树才能满足红黑树，并且这只是我们人类一看就能明白如何去旋转来达到平衡，但是计算机做不到，然后又加入了颜色这一指标（也便于指定规则来约束计算机）。

5.插入过程演化（该过程为的是更好的理解所有变化操作的情况和做法）

5-1.对在空的红黑树中插入第一个元素时，插入红色节点，由于违反第二条规定，做变色操作，变为黑色节点,如下图所示。

5-2.继续插入两个子节点，不需要任何变色操作，如下图所示。

5-3.给节点B插入左子节点D，插入后由于新节点的父节点B和叔叔C节点（祖父节点的另一个子节点）也都是红色，违反了第三条，最简单的办法就是将其父节点B和叔叔节点C变为黑色，如下图所示。

5-3.给节点D插入左子节点E，插入后首先插入节点E为红色，其父节点D为红色，且新插入的E是其父节点D的左子节点，解决办法是，首先将其父节点D变为黑色，祖父节点B变为红色，然后以祖父节点B为支点向右旋转，如下图所示。

5-4.给节点B插入右子节点F，其父节点B和叔叔节点E均为红色，将父节点B和叔叔节点E变为黑色并将其祖父节点D变成红色，如下图所示。

5-5.多插入几个节点便于后面观察，如下图所示。

5-6.给G插入左子节点K，其父节点和叔叔节点均为红色，所以将父节点和叔叔节点变为黑色且祖父节点变为红色，如下图从1变成2。这样B和D都是红色又会冲突，此时将B看作是新插入的节点，B的父节点为红色，叔叔节点为黑色，且B是其父节点的右子节点，以D为支点向左旋转，如下图3变成4(蓝色箭头代表转移的位置并不是代表连接到该节点上)。接下来D和B都是红色依然冲突，将D看着是新插入的节点，其父节点B为红色，叔叔节点C为黑色，且是其父节点B的左子节点，所以将其父节点B变为黑色，祖父节点A变为红色，并以A节点为支点向右旋转，如下图5变成6再变成7，这样整个红黑树就平衡了。