二叉树
二叉树,是一个非常重要的数据结构,在日常的开发中起着很重要的作用,它也衍生出来的各种高效的复杂的数据结构,为我们解决问题提供了高效的解决方案。
二叉树,它是由各个数据节点和左右链接构成的一种类似树的数据结构。一棵二叉树,我们只需要知道根节点,便可以访问到树中各个节点;同时树中的每一个节点,都有自身包装的数据和指向它的左右子节点的链接,如果不存在子节点,为null值,每一个节点(除去根节点)都有一个父亲节点。
节点(TreeNode)的数据结构
private class TreeNode {Data data;//节点包装的数据TreeNode left;//左节点TreeNode right;//右节点/**其他数据项**/...
}
二叉树的遍历
先序遍历
即是在进行树遍历的时候,先访问父节点,然后访问左节点,最后访问右节点。
private void preorderTraversal(TreeNode node) {if (node != null) {System.out.println("data: " + node.data);preorderTraversal(node.left);preorderTraversal(node.right);}
}
中序遍历
即是在进行树遍历的时候,先访问左节点,然后访问父节点,最后访问右节点。
private void middleTraversal(TreeNode node) {if (node != null) {middleTraversal(node.left);System.out.println("data: " + node.data);middleTraversal(node.right);}
}
后序遍历
即是在进行树遍历的时候,先访问左节点,然后访问右节点,最后访问父节点。
private void lastTraversal(TreeNode node) {if (node != null) {lastTraversal(node.left);lastTraversal(node.right);System.out.println("data: " + node.data);}
}
二叉查找树
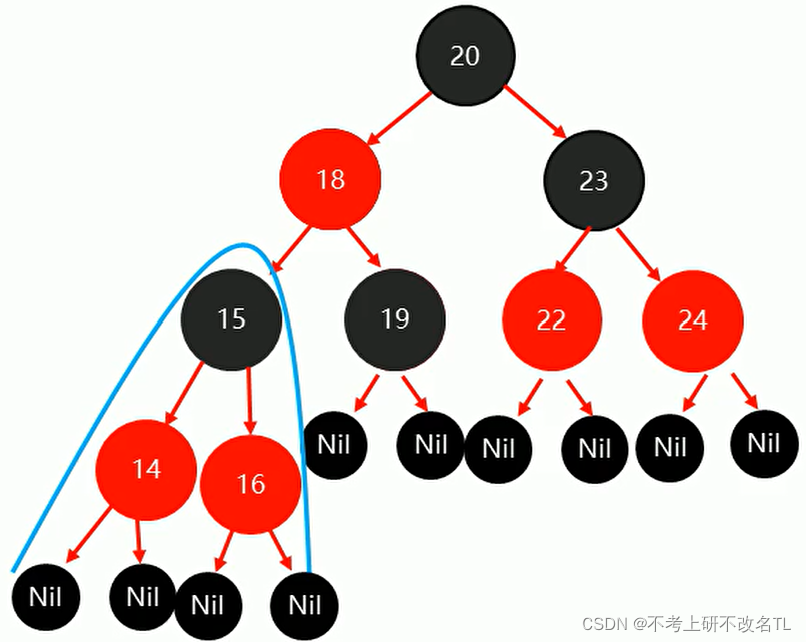
二叉查找树,顾名思义,肯定是一个方便于查找的数据结构,先看看一下二叉查找树的例子:

从上图可以很容易看出:对于每一个节点而言,它的左节点的键值(具体的可以自定义,一般为key)比它本身的键值要小,右节点的键值比它本身的大。由此构成的二叉树就是一棵二叉查询树。如果我们用中序遍历的方式来遍历该树,可以得到一个按照键值有序排列的序列。在查找一个数据节点时,会从根节点开始,用当前节点的键值与给定的键值比对,如果相同,说明当前节点即为查找节点,如果小于当前节点键值,说明待查节点在当前节点的左子树中,进而便将右子树的节点排除了,提升了查找的效率。
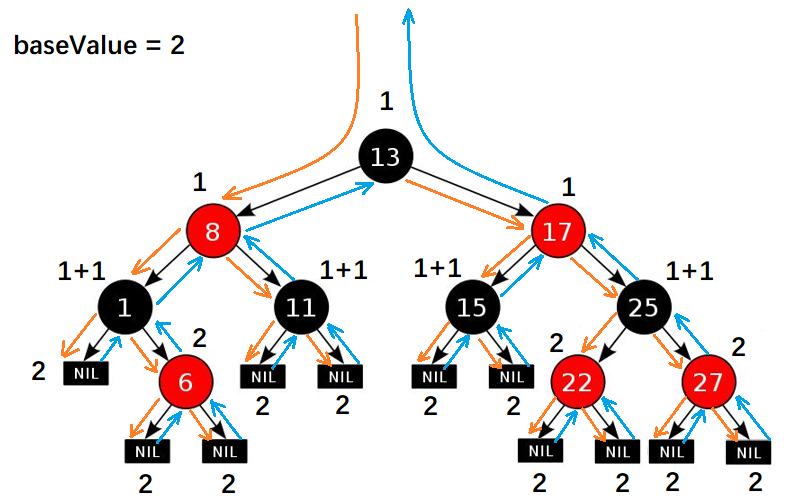
红黑树
红黑树,这是一种比较复杂的数据结构,它是
JDK1.8以后中的HashMap的底层数据结构的一个重要部分,在某些大厂的面试中也是经常出现,不知道有多少盆友都跪倒在它的脚下。

定义
红黑树是一种自平衡二叉查找树,它是基于二叉查找树设计的,具有比较高的查询效率。
性质
- 每个节点只有红和黑两种颜色
- 根节点是黑色的
- 每个红色节点的两个子节点一定是黑色节点
- 任意节点到每个叶子节点的路径包含的黑色节点的数量相同,俗称:黑高。
- 每个叶子节点都为黑色的(NIL)
节点(TreeNode)数据结构
private class TreeNode {Key key;// 键值Value value; // 数据项TreeNode left; // 左节点TreeNode right;// 右节点TreeNode parent;// 父节点int amount; // 以该节点为子树的节点总数boolean color; // 节点颜色
}
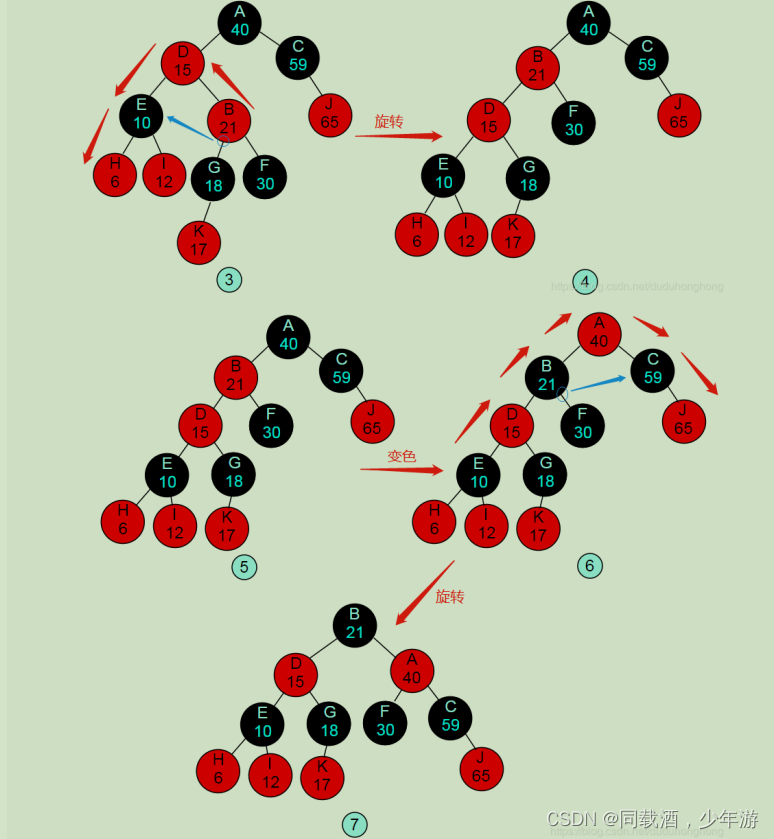
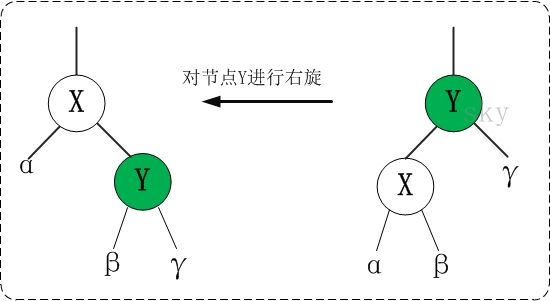
左右旋
这一部分是红黑树最难理解的部分,也是各面试官喜欢提到的点。首先要理解为哈要进行左右旋?
首先:这种操作主要是在更改树结构的时候发生,比如插入新的节点和删除一个节点,为了保证红黑树的完美平衡性,需要对树结构进行修改以满足这种要求。
这里,主要以插入来讲解一下左右旋。
首先,待插入的节点在初始化的时候,需要设置为红色。因为,如果我们以黑色的节点作为新节点插入到树中,必定会影响到树的结构,而且插入后的结构不满足红黑树的要求,必须进行旋转和变色来调整;反之,采用红色节点插入,可以避免一部分树结构调节。

虽说采用红节点作为插入节点的颜色,可以避免一定数量的树结构调节,但根据 两个红节点不能直接相连,仍然会出现需要调节树结构的情况。
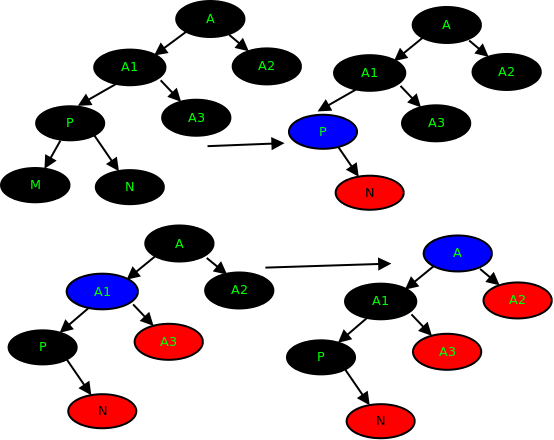
比如上图的插入节点的键值为3时,这就是一个需要调节的情况。

左右旋情况分析
-
情况一:左左(LL)

-
情况二:左右(LR)

右旋
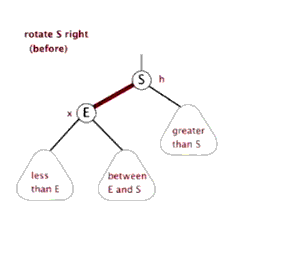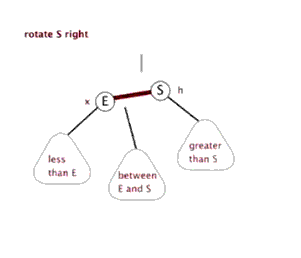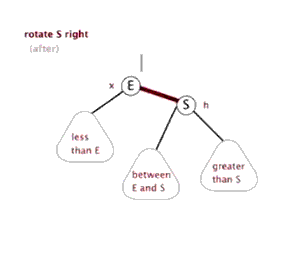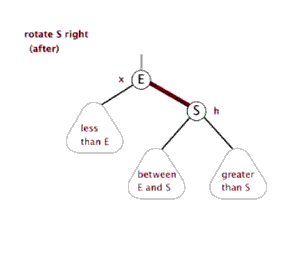
左旋
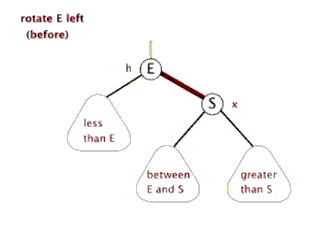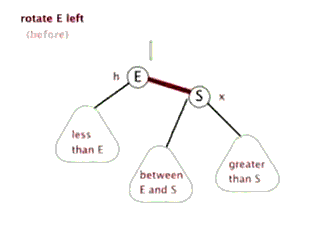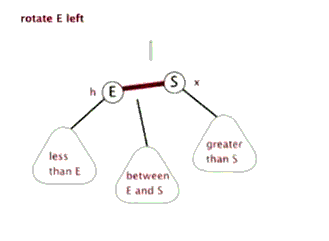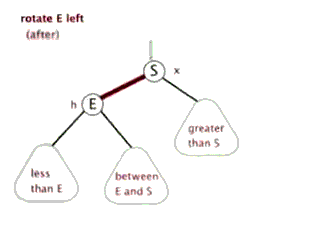
总之:在处理需要旋转的时候,我们都是把类型变为 LL 或者 RR 类型的处理。
欢迎关注公众号