二叉树系列：红黑树

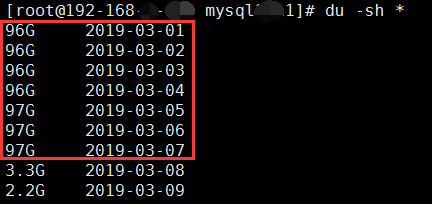
介绍

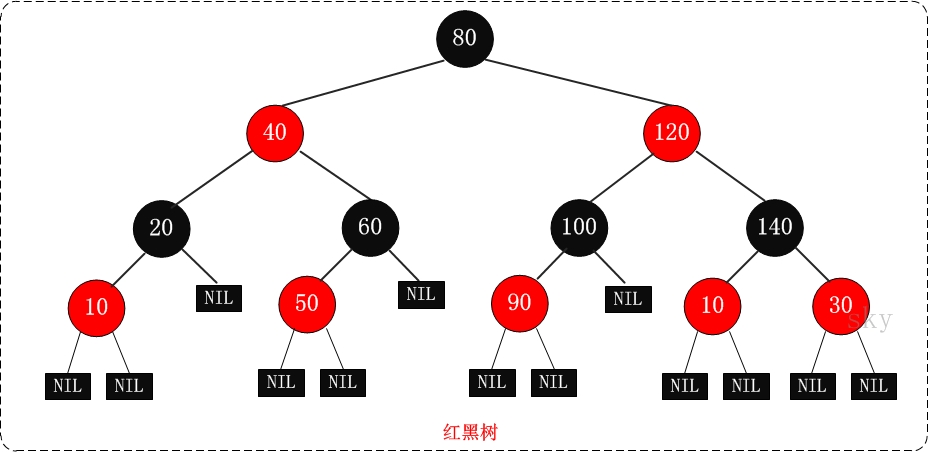
红黑树(Red-Black Tree，简称R-B Tree)，它一种特殊的二叉查找树。
红黑树是特殊的二叉查找树，意味着它满足二叉查找树的特征：任意一个节点所包含的键值，大于等于左孩子的键值，小于等于右孩子的键值。
除了具备该特性之外，红黑树还包括许多额外的信息。

红黑树的每个节点上都有存储位表示节点的颜色，颜色是红(Red)或黑(Black)。
红黑树的特性:
(1) 每个节点或者是黑色，或者是红色。
(2) 根节点是黑色。
(3) 每个叶子节点是黑色。 [注意：这里叶子节点，是指为空的叶子节点！]
(4) 如果一个节点是红色的，则它的子节点必须是黑色的。
(5) 从一个节点到该节点的子孙节点的所有路径上包含相同数目的黑节点。

关于它的特性，需要注意的是：
第一，特性(3)中的叶子节点，是只为空(NIL或null)的节点。
第二，特性(5)，确保没有一条路径会比其他路径长出俩倍。因而，红黑树是相对是接近平衡的二叉树。

二红黑树操作

常见的操作就是插入跟删除。因为红黑树的特性插入、删除会导致破坏了平衡性。所以需要修正。常见的修正操作就是颜色设置及旋转。使它重新成为红黑树。

写贴一下treemap的实现

static final class Entry<K,V> implements Map.Entry<K,V> {K key;V value;Entry<K,V> left;Entry<K,V> right;Entry<K,V> parent;boolean color = BLACK;/*** Make a new cell with given key, value, and parent, and with* {@code null} child links, and BLACK color.*/Entry(K key, V value, Entry<K,V> parent) {this.key = key;this.value = value;this.parent = parent;}
...

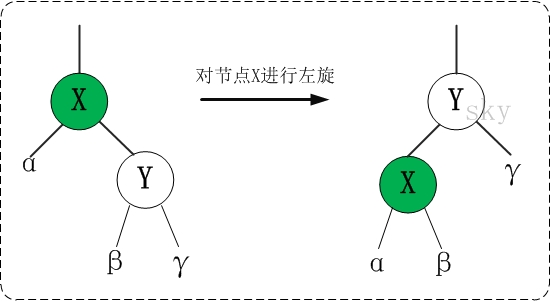
1 左旋

对x进行左旋，意味着"将x变成一个左节点"。

/** From CLR */private void rotateLeft(Entry<K,V> p) {if (p != null) {//设置p的右孩子节点为rEntry<K,V> r = p.right;// 将 “r的左孩子” 设为 “p的右孩子”；p.right = r.left;//如果r的左孩子不为空，则将p设置为“r左孩子的父亲”if (r.left != null)r.left.parent = p;//把p的父亲设置为r的父亲    r.parent = p.parent;//如果p的父亲为空，则r设为根节点if (p.parent == null)root = r;//p是它父节点的左孩子，则设置r是“p父节点的左孩子”else if (p.parent.left == p)p.parent.left = r;//p是它父节点的右孩子，则设置r是“p父节点的右孩子”elsep.parent.right = r;//p设置为r的左孩子r.left = p;//p的父节点设为rp.parent = r;}}

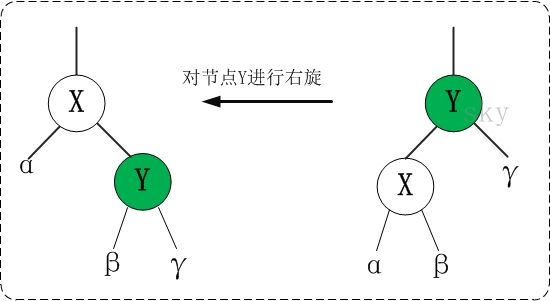
2 右旋

对y进行右旋，意味着"将y变成一个右节点"。思路同上，不再逐一注释

 /** From CLR */private void rotateRight(Entry<K,V> p) {if (p != null) {Entry<K,V> l = p.left;p.left = l.right;if (l.right != null) l.right.parent = p;l.parent = p.parent;if (p.parent == null)root = l;else if (p.parent.right == p)p.parent.right = l;else p.parent.left = l;l.right = p;p.parent = l;}}

3 插入

将一个节点插入到红黑树中，需要执行哪些步骤呢？首先，将红黑树当作一颗二叉查找树，将节点插入；然后，将节点着色为红色；最后，通过"旋转和重新着色"等一系列操作来修正该树，使之重新成为一颗红黑树。详细描述如下：
第一步: 将红黑树当作一颗二叉查找树，将节点插入。
红黑树本身就是一颗二叉查找树，将节点插入后，该树仍然是一颗二叉查找树。也就意味着，树的键值仍然是有序的。此外，无论是左旋还是右旋，若旋转之前这棵树是二叉查找树，旋转之后它一定还是二叉查找树。这也就意味着，任何的旋转和重新着色操作，都不会改变它仍然是一颗二叉查找树的事实。
好吧？那接下来，我们就来想方设法的旋转以及重新着色，使这颗树重新成为红黑树！

第二步：将插入的节点着色为"红色"。

第三步: 通过一系列的旋转或着色等操作，使之重新成为一颗红黑树。
第二步中，将插入节点着色为"红色"之后，不会违背"特性(5)"。那它到底会违背哪些特性呢？
对于"特性(1)"，显然不会违背了。因为我们已经将它涂成红色了。
对于"特性(2)"，显然也不会违背。在第一步中，我们是将红黑树当作二叉查找树，然后执行的插入操作。而根据二叉查找数的特点，插入操作不会改变根节点。所以，根节点仍然是黑色。
对于"特性(3)"，显然不会违背了。这里的叶子节点是指的空叶子节点，插入非空节点并不会对它们造成影响。
对于"特性(4)"，是有可能违背的！

那接下来，想办法使之"满足特性(4)"，就可以将树重新构造成红黑树了。

下面是treemap的实现方式

public V put(K key, V value) { Entry<K,V> t = root; // 一个空链表if (t == null) { root = new Entry<K,V>(key, value, null); size = 1; // 记录修改次数为 1 modCount++; return null; } int cmp; Entry<K,V> parent; Comparator<? super K> cpr = comparator; // 采用定制排序if (cpr != null) { do { parent = t; cmp = cpr.compare(key, t.key); if (cmp < 0) t = t.left; else if (cmp > 0) t = t.right; else return t.setValue(value); } while (t != null); } else { if (key == null) throw new NullPointerException(); Comparable<? super K> k = (Comparable<? super K>) key; do {  parent = t; cmp = k.compareTo(t.key); if (cmp < 0) t = t.left; else if (cmp > 0) t = t.right; else return t.setValue(value); } while (t != null); } // 将新插入的节点作为 parent 节点的子节点Entry<K,V> e = new Entry<K,V>(key, value, parent); if (cmp < 0) parent.left = e; else parent.right = e; // 修复红黑树fixAfterInsertion(e);                               size++; modCount++; return null; }

private void fixAfterInsertion(Entry<K,V> x) { x.color = RED; //设新插入的为红色，对应第二步// 直到 x 节点的父节点不是根，且 x 的父节点不是红色while (x != null && x != root && x.parent.color == RED) { //  x 的父节点是其父节点的左子节点if (parentOf(x) == leftOf(parentOf(parentOf(x)))) { // 获取 x 的父节点的兄弟节点Entry<K,V> y = rightOf(parentOf(parentOf(x))); // 如果 x 的父节点的兄弟节点是红色(需要颜色翻转)if (colorOf(y) == RED) { // 将 x 的父节点设为黑色setColor(parentOf(x), BLACK); // 将 x 的父节点的兄弟节点设为黑色setColor(y, BLACK); // 将 x 的父节点的父节点设为红色setColor(parentOf(parentOf(x)), RED); x = parentOf(parentOf(x)); } // 如果 x 的父节点的兄弟节点是黑色（需要旋转）else { // 如果 x 是其父节点的右子节点if (x == rightOf(parentOf(x))) { // 将 x 的父节点设为 x x = parentOf(x); rotateLeft(x); } // 把 x 的父节点设为黑色setColor(parentOf(x), BLACK); // 把 x 的父节点的父节点设为红色setColor(parentOf(parentOf(x)), RED); rotateRight(parentOf(parentOf(x))); } } // 以下的操作是上面操作的对称，就不做分析了else { Entry<K,V> y = leftOf(parentOf(parentOf(x))); if (colorOf(y) == RED) { setColor(parentOf(x), BLACK); setColor(y, BLACK); setColor(parentOf(parentOf(x)), RED); x = parentOf(parentOf(x)); } else { if (x == leftOf(parentOf(x))) { x = parentOf(x); rotateRight(x); } setColor(parentOf(x), BLACK); setColor(parentOf(parentOf(x)), RED); rotateLeft(parentOf(parentOf(x))); } } } // 将根节点设为黑色root.color = BLACK; }

其中的parentof是获取父节点。这里需要结合别的资料来展开这么多判断场景。我也忘了。

4 删除

之前二叉树就删除是个复杂操作，因为删除对应不同的情况。

红黑树也不例外：

将红黑树当作一颗二叉查找树，将该节点从二叉查找树中删除；然后，通过"旋转和重新着色"等一系列来修正该树，使之重新成为一棵红黑树。详细描述如下：
第一步：将红黑树当作一颗二叉查找树，将节点删除。
这和"删除常规二叉查找树中删除节点的方法是一样的"。分3种情况：
① 被删除节点没有儿子，即为叶节点。那么，直接将该节点删除就OK了。
② 被删除节点只有一个儿子。那么，直接删除该节点，并用该节点的唯一子节点顶替它的位置。
③ 被删除节点有两个儿子。那么，先找出它的后继节点；然后把“它的后继节点的内容”复制给“该节点的内容”；之后，删除“它的后继节点”。我们队红黑树删除的操作，每一件事情都归咎于能够删除树叶。这是因为要删除带有两个孩子节点的可以用右子树的最小节点代替它

第二步：通过"旋转和重新着色"等一系列来修正该树，使之重新成为一棵红黑树。
因为"第一步"中删除节点之后，可能会违背红黑树的特性。所以需要通过"旋转和重新着色"来修正该树，使之重新成为一棵红黑树。

    /*** Delete node p, and then rebalance the tree.*/private void deleteEntry(Entry<K,V> p) {modCount++;size--;// If strictly internal, copy successor's element to p and then make p// point to successor.if (p.left != null && p.right != null) {// 用 p 节点的中序后继节点代替 p 节点Entry<K,V> s = successor(p);p.key = s.key;p.value = s.value;p = s;} // p has 2 children// Start fixup at replacement node, if it exists.Entry<K,V> replacement = (p.left != null ? p.left : p.right);if (replacement != null) {// Link replacement to parentreplacement.parent = p.parent;if (p.parent == null)root = replacement;else if (p == p.parent.left)p.parent.left  = replacement;elsep.parent.right = replacement;// Null out links so they are OK to use by fixAfterDeletion.p.left = p.right = p.parent = null;// Fix replacementif (p.color == BLACK)fixAfterDeletion(replacement);//修复红黑树} else if (p.parent == null) { // return if we are the only node.root = null;} else { //  No children. Use self as phantom replacement and unlink. 代替节点为空的情况if (p.color == BLACK)fixAfterDeletion(p);if (p.parent != null) {if (p == p.parent.left)p.parent.left = null;else if (p == p.parent.right)p.parent.right = null;p.parent = null;}}}

下面是修复方法。修复的过程中分为四种情况：
1、N的兄弟节点W为红色
2、N的兄弟w是黑色的，且w的俩个孩子都是黑色的。
3、N的兄弟w是黑色的，w的左孩子是红色，w的右孩子是黑色。
4、N的兄弟w是黑色的，且w的右孩子时红色的。

/ 删除节点后修复红黑树private void fixAfterDeletion(Entry<K,V> x) { // 直到 x 不是根节点，且 x 的颜色是黑色while (x != root && colorOf(x) == BLACK) { // 如果 x 是其父节点的左子节点if (x == leftOf(parentOf(x))) { // 获取 x 节点的兄弟节点Entry<K,V> sib = rightOf(parentOf(x)); // 如果 sib 节点是红色if (colorOf(sib) == RED) { // 将 sib 节点设为黑色setColor(sib, BLACK); // 将 x 的父节点设为红色setColor(parentOf(x), RED); rotateLeft(parentOf(x)); // 再次将 sib 设为 x 的父节点的右子节点sib = rightOf(parentOf(x)); } // 如果 sib 的两个子节点都是黑色if (colorOf(leftOf(sib)) == BLACK && colorOf(rightOf(sib)) == BLACK) { // 将 sib 设为红色setColor(sib, RED); // 让 x 等于 x 的父节点x = parentOf(x); } else { // 如果 sib 的只有右子节点是黑色if (colorOf(rightOf(sib)) == BLACK) { // 将 sib 的左子节点也设为黑色setColor(leftOf(sib), BLACK); // 将 sib 设为红色setColor(sib, RED); rotateRight(sib); sib = rightOf(parentOf(x)); } // 设置 sib 的颜色与 x 的父节点的颜色相同setColor(sib, colorOf(parentOf(x))); // 将 x 的父节点设为黑色setColor(parentOf(x), BLACK); // 将 sib 的右子节点设为黑色setColor(rightOf(sib), BLACK); rotateLeft(parentOf(x)); x = root; } } // 下面是上面的对称操作就不做具体分析了else { Entry<K,V> sib = leftOf(parentOf(x)); if (colorOf(sib) == RED) { setColor(sib, BLACK); setColor(parentOf(x), RED); rotateRight(parentOf(x)); sib = leftOf(parentOf(x)); } if (colorOf(rightOf(sib)) == BLACK && colorOf(leftOf(sib)) == BLACK) { setColor(sib, RED); x = parentOf(x); } else { if (colorOf(leftOf(sib)) == BLACK) { setColor(rightOf(sib), BLACK); setColor(sib, RED); rotateLeft(sib); sib = leftOf(parentOf(x)); } setColor(sib, colorOf(parentOf(x))); setColor(parentOf(x), BLACK); setColor(leftOf(sib), BLACK); rotateRight(parentOf(x)); x = root; } } } setColor(x, BLACK); }

Treemap里面还有很多其他公用方法，下面是测试结果：

package com.daojia.collect;import java.util.Iterator;
import java.util.NavigableMap;
import java.util.Set;
import java.util.TreeMap;public class TreeMapTest {private static final int a[] = {10, 40, 30, 60, 90, 70, 20, 50, 80};public static void main(String[] args) {int i, ilen = a.length;TreeMap tree=new TreeMap();System.out.printf("== 原始数据: ");for(i=0; i<ilen; i++)System.out.printf("%d ", a[i]);System.out.printf("\n");for(i=0; i<ilen; i++) {tree.put(a[i],a[i]);		        System.out.printf("== 添加节点: %d\n", a[i]);System.out.printf("== 树的详细信息: \n");		              System.out.printf(  tree.toString()+"\n");}System.out.printf("遍历: ");		      Set<Integer> keys = tree.keySet();for (Integer key : keys){System.out.println(key);}System.out.printf("== 最小值: %s\n", tree.firstEntry().getValue());System.out.printf("== 最大值: %s\n", tree.lastEntry().getValue());tree.remove(a[5]);System.out.printf("== 删除节点: %d\n", a[5]);System.out.printf("== 树的详细信息: \n");System.out.printf(   tree.toString()+"\n");// 销毁二叉树NavigableMap  nmap =tree.descendingMap();Iterator iterator = nmap.keySet().iterator();while (iterator.hasNext()) {Integer key = (Integer) iterator.next();// 获取ValueSystem.out.println(tree.get(key));}}}

== 原始数据: 10 40 30 60 90 70 20 50 80
== 添加节点: 10
== 树的详细信息:
{10=10}
== 添加节点: 40
== 树的详细信息:
{10=10, 40=40}
== 添加节点: 30
== 树的详细信息:
{10=10, 30=30, 40=40}
== 添加节点: 60
== 树的详细信息:
{10=10, 30=30, 40=40, 60=60}
== 添加节点: 90
== 树的详细信息:
{10=10, 30=30, 40=40, 60=60, 90=90}
== 添加节点: 70
== 树的详细信息:
{10=10, 30=30, 40=40, 60=60, 70=70, 90=90}
== 添加节点: 20
== 树的详细信息:
{10=10, 20=20, 30=30, 40=40, 60=60, 70=70, 90=90}
== 添加节点: 50
== 树的详细信息:
{10=10, 20=20, 30=30, 40=40, 50=50, 60=60, 70=70, 90=90}
== 添加节点: 80
== 树的详细信息:
{10=10, 20=20, 30=30, 40=40, 50=50, 60=60, 70=70, 80=80, 90=90}
遍历: 10
20
30
40
50
60
70
80
90
== 最小值: 10
== 最大值: 90
== 删除节点: 70
== 树的详细信息:
{10=10, 20=20, 30=30, 40=40, 50=50, 60=60, 80=80, 90=90}
90
80
60
50
40
30
20
10

参考：

https://www.cnblogs.com/skywang12345/p/3624343.html