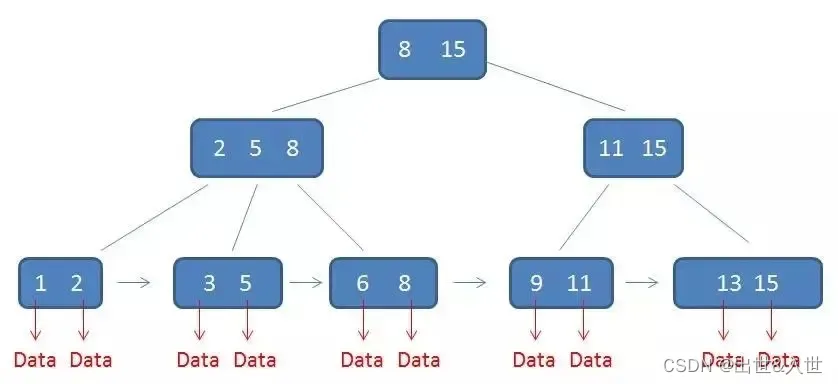
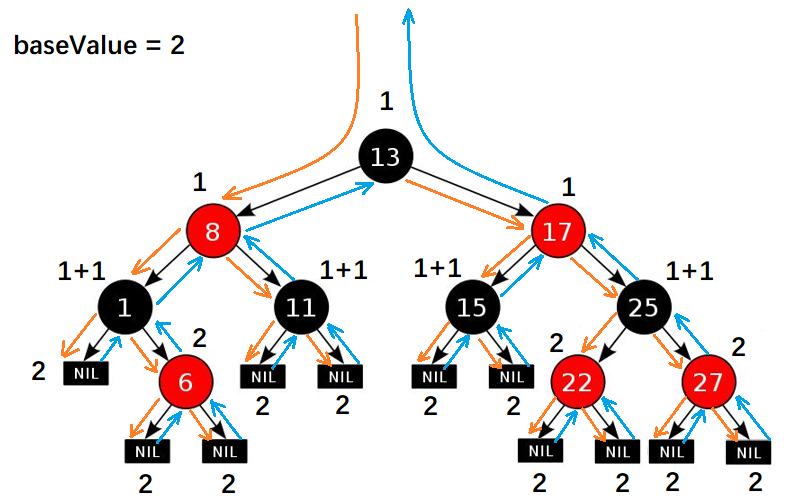
1.红黑树定义
红黑树是一颗 红-黑的平衡二叉树,它具有二叉树的所有特性,是一颗自平衡的排序二叉树.(树中任何节点值都大于左子节点的值,而且都小于右子节点的值),其检索效率高,它是一颗空树或它的左右两个子树高度差的绝对值不超过1,并且左右子树都是平衡二叉树.

最坏的情况下 是一边倒的情况

在这种情况下,如果我们要在树中查找g节点,就需要顺着根节点往下找,时间复杂度约为O(n)常数级。那么红黑树具有以下特点,使得它的查找时间复杂度为O(lg n)

性质
1.每一个节点 必须为红色或者黑色
2.根节点是黑色的
3.每个叶子节点(nil节点 空节点是黑色的)
4.如果一个节点是红色的,那么它的叶子节点都是黑色的(同一个路径下 不允许出现两个相邻的红色节点)
5.对于任一结点而言,其到叶结点树尾端NIL指针的每一条路径都包含相同数目的黑结点(黑节点的数目称为黑高black-height)
从根到叶子节点的最大路径不能大于最短路径的两倍长,大致上是平衡的,插入、删除和查找某个值的最坏情况时间都要求与树的高度成比例。
如果查找、插入、删除频率差不多,那么选择红黑树。
插入
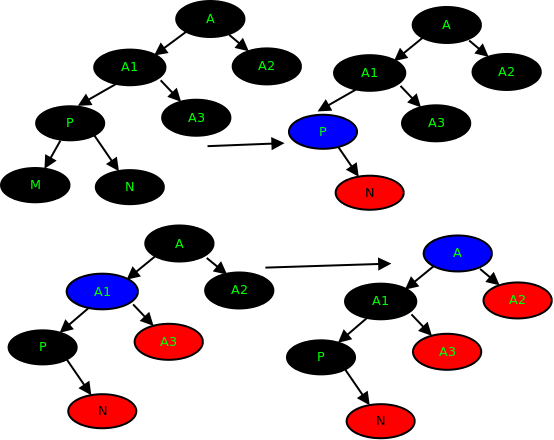
口诀:所有插入为红色,父红叔红变颜色 ,父红叔黑右子树 以父为心向左旋 ,父红叔黑左子树 变父为黑爷为红 以爷为心向右旋
默认插入的节点为红色,因为黑色节点的数量为红色节点数量的两倍多,因此插入节点的父节点为黑色的概率很大,不需要做任何调整,效率较高.
1.父为黑
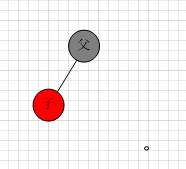
这种情况下,直接插入,且插入后无需任何操作,黑色节点的数量多与红色节点的数量(2倍左右),因此父为黑这种概率比较大,效率比AVL树高。
2.父为红
这种情况破坏了红黑树的特点(相同路径下不能出现两个相邻的红色节点),因此,因此要跟据叔叔的颜色 做不同的插入处理

图中叔叔的颜色也有两种可能 暂时以蓝色表示
1),叔叔为红

2),叔叔为黑(这种情况有比较复杂)
a.父在左,叔叔在右,新节点在左

b,父在左 叔叔在右,新在右

c,父在右,叔在左 ,新在右

d,父在右,叔叔在左,新在左

删除
删除一颗普通的二叉排序树 有三种情况
1.叶子节点
2.只有左子树或只有右子树的节点
3.既有左子树 又有右子树的节点
对于情况3来讲,我们的思路是先找到待删除节点的后继节点(左孩子节点或右孩子节点),然后用孩子节点的值将待删除节点的值覆盖,最后按1,2中的方法删除孩子节点即可
对情况2来讲,待删除节点只有左子树或右子数,有很多组合,在红黑树中是不存在的,违背了红黑树的性质,图中 C代表待删节点,CR表示右孩子,CL表示左孩子

图中这四种情况都违背了红黑树性质5,不会存在

此图中 违背了性质4
1,待删除的节点为红色
C 代表要删除的节点,P代表父节点

上面这两种情况 处理方式都一样,直接删除C就好
另外待删除的红色节点,只有左子树或右子树 这种情况是不存在的(已探讨)
2,接下来,讨论最复杂的情况,待删除的节点为黑色节点
a,删除黑色的叶子节点

这种情况相对复杂,后面细分
删除的黑色节点 仅有左子树或仅有右子树

对于这种情况,我们用子节点覆盖调节点C,并且将C 的子节点的颜色改为黑色 ,(因此路径上少了一个黑节点,所以将红色节点变为黑色节点以保证红黑树的性质)
a.1:待删除的叶子节点兄弟节点为红色

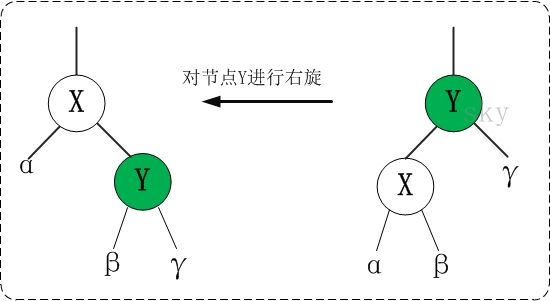
c为父节点的左子节点的情况,做法是将兄弟节点b和父节点p的颜色互换,同时将兄弟节点p左旋转

此时C的兄弟节点变成了黑色 这就是我们后面要讨论的情况
c是右子节点的情况,同上,将兄弟节点b和父节点p的颜色互换,同时将兄弟节点p右旋转


此时c的兄弟节点也变成了黑色 ,这也是我们后面要谈论的情况
a.2:兄弟节点为黑色,且远侄子节点为红色
c为左孩子的情况,这时c的远侄子节点为b的右孩子

没有上色的节点表示为红黑均可,如果bL为黑色,则bL则必为null节点,如果删除c,那么经过c节点的黑节点个数就少一个,但如果我们能把bR节点移到左侧,并改为黑色,就满足红黑树的特点了,(p节点的颜色不影响,因为整个调整过程是在p子树内部进行的)
调整过程为将b和p颜色对调,将b进行左旋转(L操作),同时将远侄子节点bR变为黑色,删除掉c

c为右孩子的情况,此时c的远侄子为b的左孩子

同样,将b节点和p节点颜色对调,然后将以b节点为起始,向右旋转,将c的远侄子节点bL变成黑色 删除掉c

a.3:兄弟节点为黑色,远侄子节点为黑色,近侄子节点为红色.
c为左孩子,近侄子节点为兄弟节点的左孩子
此时将bL节点右旋(R操作),将b节点和bL节点颜色对调

这时候就变成了a.4的情况
c为右孩子,近侄子节点为兄弟节点的右孩子 且为红节点

做法是将bL节点左旋(L操作),将b节点和bL节点颜色对调

这样就变成了a.4
a.4:父亲节点为红色,且兄弟节点和兄弟节点的两个孩子节点(只能是null节点)都为黑色 的情况

如果删除节点c,那么经过p和c的节点的黑节点就少了一个,这个时候我们可以把p变为黑色,这个时候 删除c节点经过c的子节点(空节点)的路径上的黑节点就和原来一样了,但是经过b节点的路径上就多了一个黑节点,所以我们可以把b变成红节点,这样经过b的路径上的黑色节点就和原来一样了
做法是 将父节点p变成黑色,将b节点变成红色

a.5:父亲节点,兄弟节点 以及兄弟节点的孩子(只能是null节点)都为黑色的情况

方法是将b节点改为红色,这样删除c以后p的左右子树上的黑节点的个数就相同了,但是这样 经过b节点的路径上的黑节点就少了一个,这个时候,我们再以p为起始点,继续根据情况进行平衡操作(这句话的意思就是把p当成c(只是不要再删除p了),再看是那种情况,再进行对应的调整,这样一直向上,直到新的起始点为根节点)
网页工具:https://www.cs.usfca.edu/~galles/visualization/RedBlack.html


判断类型的时候,先看待删除的节点的颜色,再看兄弟节点的颜色,再看侄子节点的颜色(侄子节点先看远侄子再看近侄子),最后看父亲节点的颜色
开始写代码了