直接或间接地调用自身的算法称为递归算法。

通过这种递推关系把原来问题缩小成一个更小规模的同类问题，并延续这一缩小规模的过程，直到在某一规模上，问题的解是已知的。这样一种解决问题的思想我们称为递归的思想。

常见题目1：

求n的阶乘

        

上面的代码是不是就印证了当问题缩小到一定的规模的时候，问题是有解的，像上面这个问题，当n==1的时候，题目就是有解的。

下面来说一下递归需要注意的两点：

第一，递归必须有递推关系，比如上面这道题的递推关系就是n与n-1的一个递推关系，比如求n的阶乘就是求n*(n-1)!的阶乘

第二，必须有结束条件，也就是当问题缩小到一定的规模的时候，问题是有解的。

下面我们说一个问题：栈与递归

这里就不得不来说一下，函数调用栈，什么是函数调用栈，就是函数会在栈上面开辟一个栈来保存如下信息：

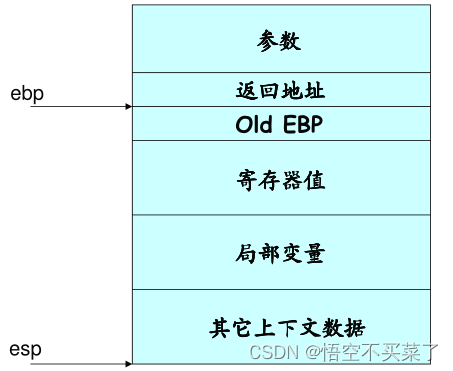
栈我们必须要知道，栈底是高地址，栈顶是地址，栈的增长方向永远是从栈底往栈顶增长，下面看一下一个函数的调用

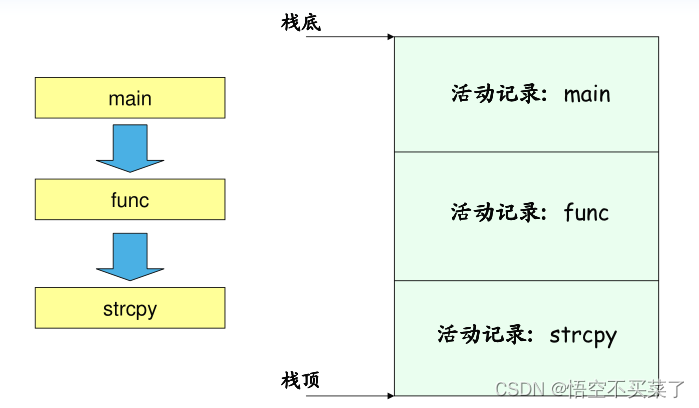
 先遇到什么函数，很明显就是先入栈，main是程序入口，肯定先入栈，然后main内部又调用了func，又会把func入栈，func又调用了strcpy函数，strcpy又会入栈，最后在从栈顶向外弹出栈，弹出strcpy函数，又弹出func函数，然后弹出main函数。就是这么一个函数执行过程。

下面我们看一个代码，逆序打印字符串：

#include <stdio.h>
#include <stdlib.h>//利用递归逆序打印字符串
void reverse_print(char *s)
{//必须有结束条件if(s != NULL && *s != '\0') {reverse_print(s+1);//指针往下面轮替printf("%c",*s);} else {return; }
}int main() 
{char *s = "ABCDE";reverse_print(s);return 0;
}

        

         我们利用递归思想分析一下：

        

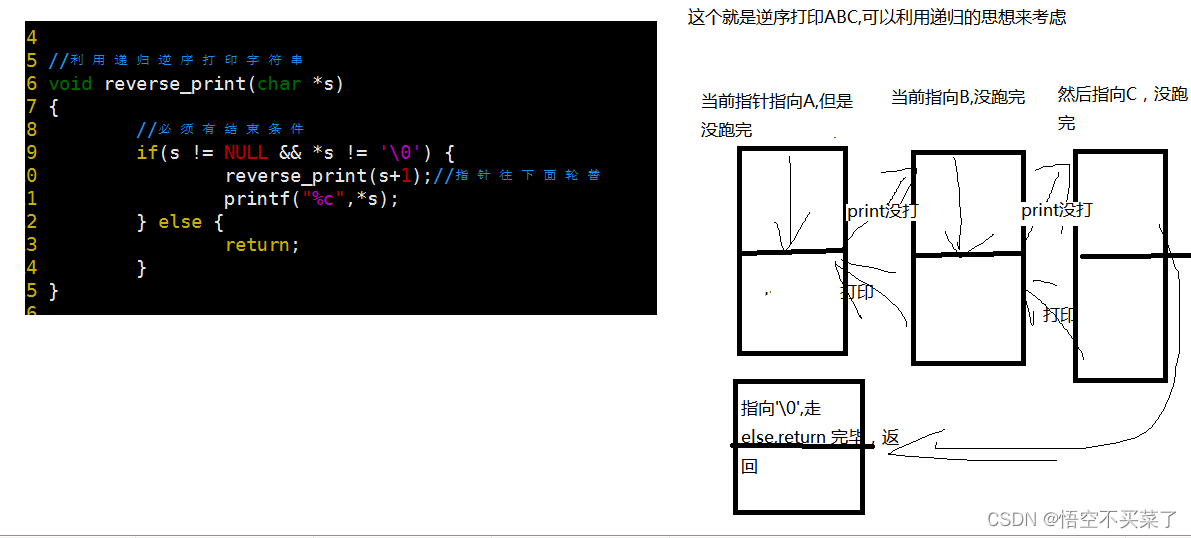
我们也可以用函数调用栈来分析一下：

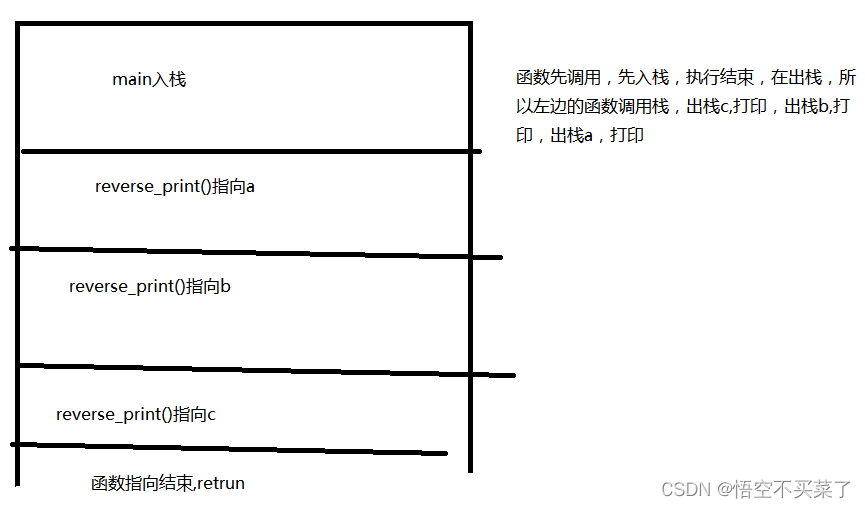
OK，以上就是递归分析过程。

下面来看几个习题：

递归1：打印某个位置的斐波拉契数列

直接上代码：

        

#include <stdio.h>
#include <stdlib.h>//斐波拉契数列
int fibonacci(int n)
{//结束条件，递推条件if(n == 1 || n== 2) {return 1;} else {return fibonacci(n-1) + fibonacci(n-2);}
}int main()
{//输入前十个数据for(int i = 1;i <= 10;i++) {printf("f(%d)=%d\n",i,fibonacci(i));}return 0;
}

 运行结果：
        

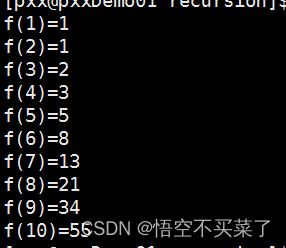
讲解一下过程：

         

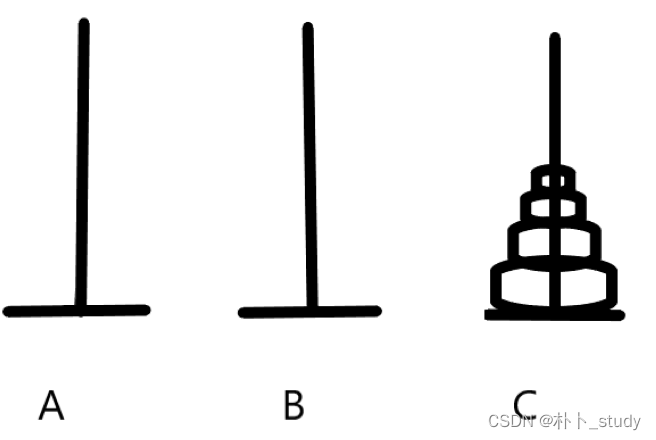
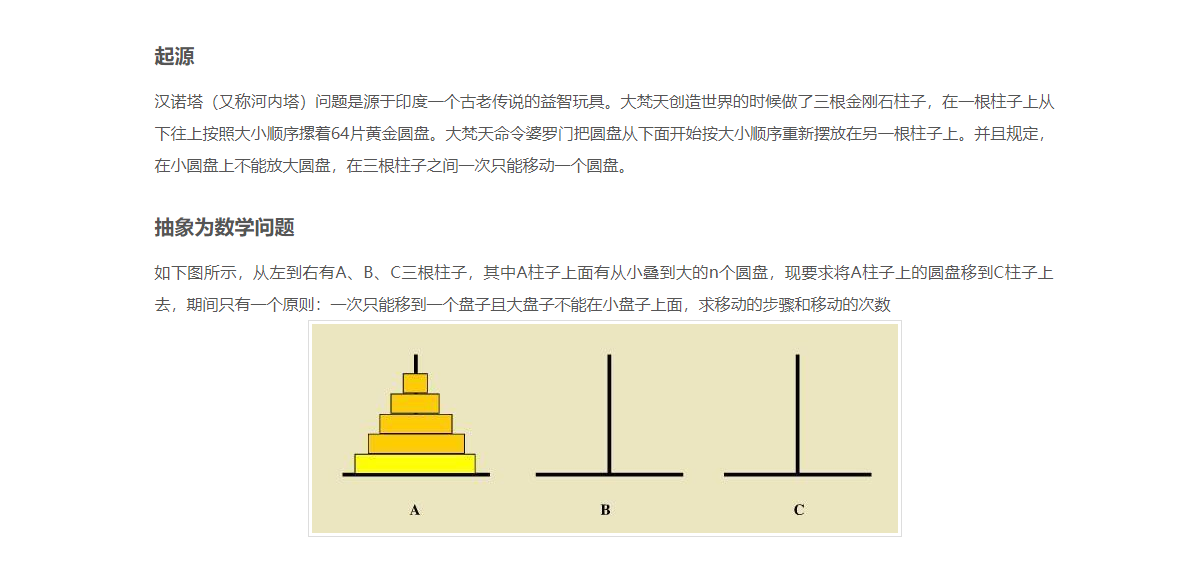
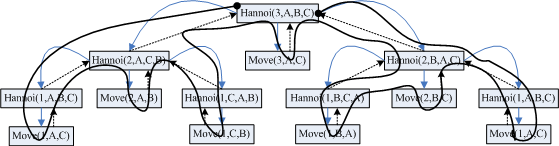
递归2：汉诺塔问题求解

         首先来分析这个汉诺塔有没有一个递归的过程。

        先来看一个盘子：

                

        直接从A->C

         再来看两个盘子：

        

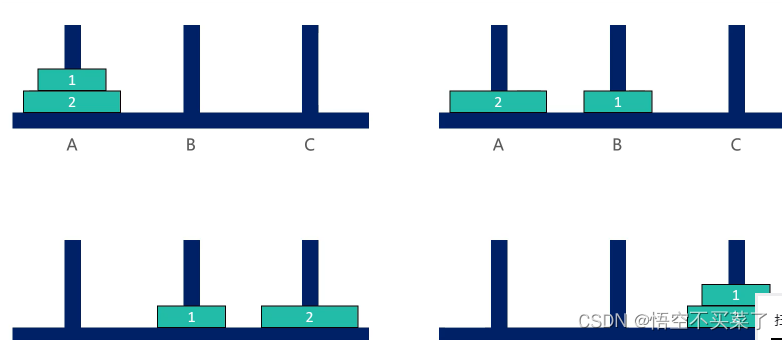
        很明显是先先把上面n-1的移动到B柱，也就是A->B

        然后n带到C,A->C

        最后B,也就是n-1移动到C ,B->C

        再来看三个盘子：

        

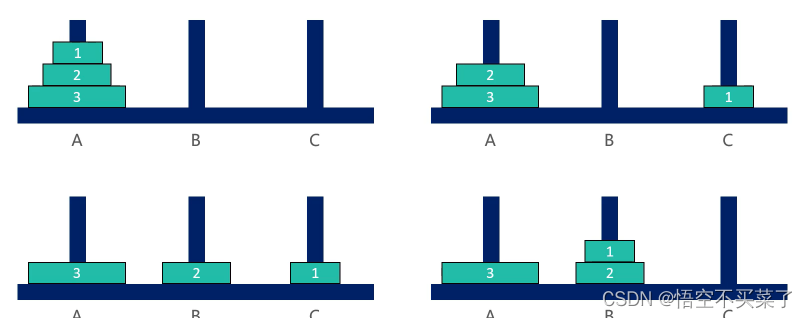
        还是把n-1的盘子从A->B

        然后把n从A->C

        最后把B上的n-1从B->C

        四个盘子，五个盘子都是按照这样来考虑

        也就是形成了一个递归过程：

                分析这样的问题，删繁就简，1个盘子太特殊，我们选择2个盘子来进行分析：

                 

        上面最关键就是注意参数的位置。原始是h(n,a,b,c),在递归的时候，注意按照打印顺序变换参数的位置。另外就是上面的代码明显分两部分递归，一部分，从A->B，另外一部分，从B->C，中间是n的一个A->C一个固定表达

        下面直接上代码

#include <stdio.h>
#include <stdlib.h>void hanoi(int n,char a,char b,char c) 
{if(n == 1) {printf("%d号盘从%c->%c\n",n,a,c);//这个是参数，不代表实际a与c柱子} else {//先从A->B//此时c参数的位置就是B盘hanoi(n-1,a,c,b);//从a->b//中间固定步骤a->cprintf("%d号盘从%c->%c\n",n,a,c);//另外一部分的递归循环从B->Chanoi(n-1,b,a,c);//改变盘的位置}
}int main()
{hanoi(3,'A','B','C');return 0;
}

        汉诺塔最主要是从宏观角度分析，而不是去研究四个盘子的具体移动，五个盘子的具体移动等等这样的问题。

        下面来说一个全排列的问题：

                这里我们就来说一下字符串的全排列

                就比如如下：

                        

                那我们来分析一下全排列有没有一种递推关系

                当只有1个字符的时候，全排列是自己，这个其实就可以作为递归的结束条件

                当有两个字符，那么首先分别拿出A、B,然后又给自依赖第一个字符的全排列

                当有三个字符，那么先拿出A字符，依赖于BC的全排列，也就是两个字符的全排列，然 后BC又依赖于1个字符的全排列

                依次往下类推，也就是后面的全排列依赖于前面数据的全排列，这个也就是我们的递推关系

                 

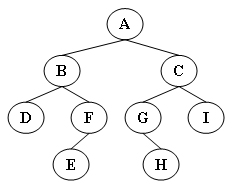
具体分析图如下：

         

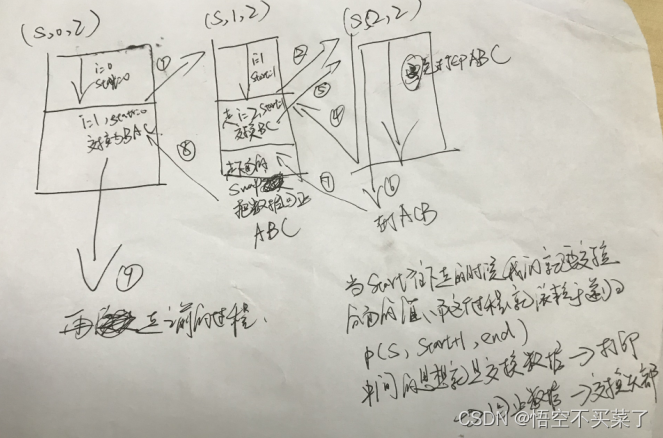
 以上就是思考过程，最关键的是递归我们必须有全局意识，比如全排列，结束就是start=end,打印，然后一直往下面递归，全排列，然后回来的时候交换位置回到主位置，方便开头字母交换全排，中间记得循环目标数组，不然交换不了。

话不多说，上代码：

        

#include <stdio.h>//交换函数
void swap(char *str,int i,int j)
{char c = str[i];str[i] = str[j];str[j] = c; 
}//全排列
void permutation(char *str,int start,int end)
{//递归函数的结束条件if(start == end) {printf("%s\n",str);} else {//循环置换整个字符串for(int i = start;i <= end;i++) {//每次回来我们置换A,B,C头部，保持start不懂，i++swap(str,i,start);//start在整体循环中是不动的start = 0;i循环//开始轮替后面的数据permutation(str,start + 1,end);//回来的首把数据回到原始样子比如ABC进来，就ABC回来//回正的目的是为了我们开头的头部交换swap(str,i,start);				}}
}int main()
{char s[] = "ABC";permutation(s,0,2);return 0;
}

结果：

        

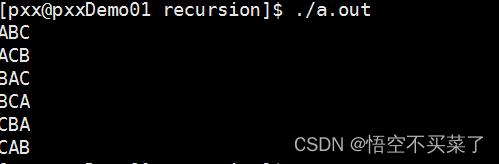
 下面再来说一个strlen递归求解问题：

        这个也就是利用递归来解决求字符串长度的问题

        这个相对来说简单，直接上代码：

        

#include <stdio.h>
#include <stdlib.h>
#include <string.h>int my_strlen(char *str)
{if(str == NULL) {return -1;}if(*str == '\0') {return 1;} else {return my_strlen(str + 1) + 1;}
}int main()
{const char *s = "ABCD";int res = strlen(s);printf("%d\n",res);return 0;
}

下面我们来说递归当中的一个经典问题：

        八皇后问题：

                

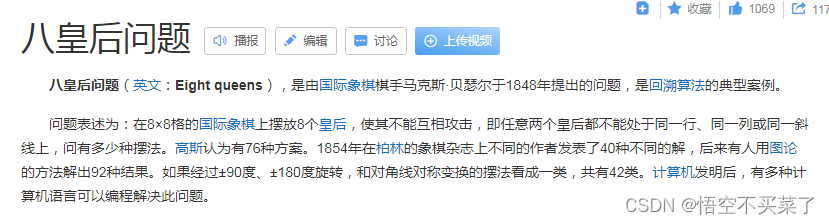
        解题思路分析：

        

 

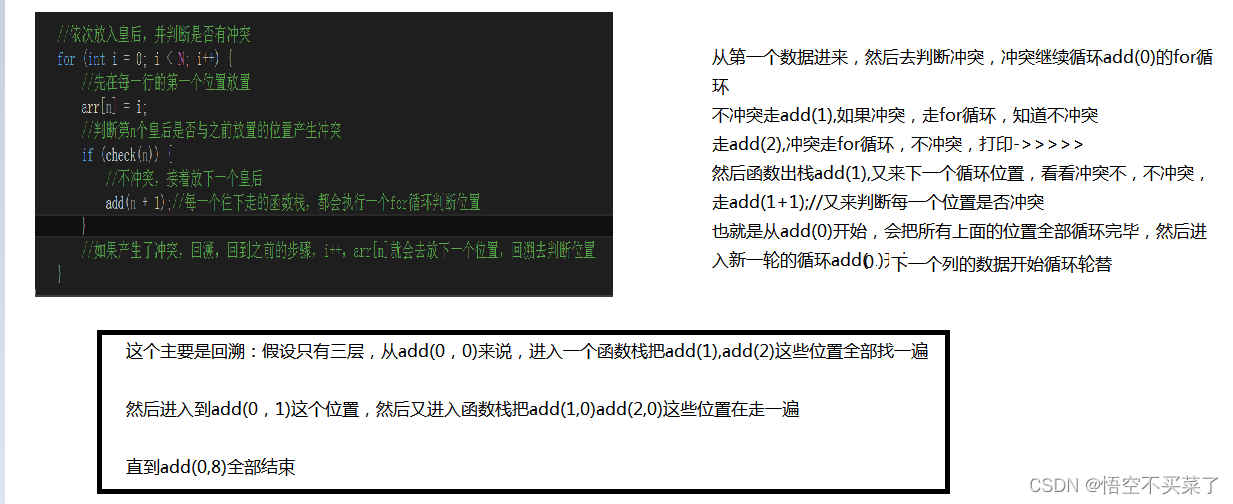
下面直接上代码：

#include <stdio.h>
#include <stdlib.h>
#define N 8static int arr[N];//定义一个存放八皇后的全局数组
static int count = 0;//判断皇后插入问题是否正确
int check(int n)
{//与之前插入的每一个皇后做一个对比//因为n就代表第几个皇后，同时也代表第几行//这里n从0开始算,比如第三个就是2,然后去判断与0、1行插入的位置是否合理for (int i = 0; i < n; i++) {//如果是同一列，或者同一斜线if ((arr[i] == arr[n]) || (abs(n - i) == abs(arr[n] - arr[i]))) {return 0;}}//上面都没进去，就返回一个真return 1;
}//打印这个数组
void myPrint() 
{for (int i = 0; i < 8; i++) {printf("%d ", arr[i]);}printf("\n");
}//编写方法，放置n个皇后//开始进行递归插入
void add(int n)
{if (n == N) {myPrint();//n=8的时候说明每个位置都放好了count++;return;}//依次放入皇后，并判断是否有冲突for (int i = 0; i < N; i++) {//先在每一行的第一个位置放置arr[n] = i;//判断第n个皇后是否与之前放置的位置产生冲突if (check(n)) {//不冲突，接着放下一个皇后add(n + 1);//每一个往下走的函数栈，都会执行一个for循环判断位置}//如果产生了冲突，回溯，回到之前的步骤，i++，arr[n]就会去放下一个位置，回溯去判断位置}
}void main()
{add(0);printf("一共%d个解法\n", count);system("pause");
}

 运行结果部分截图： 

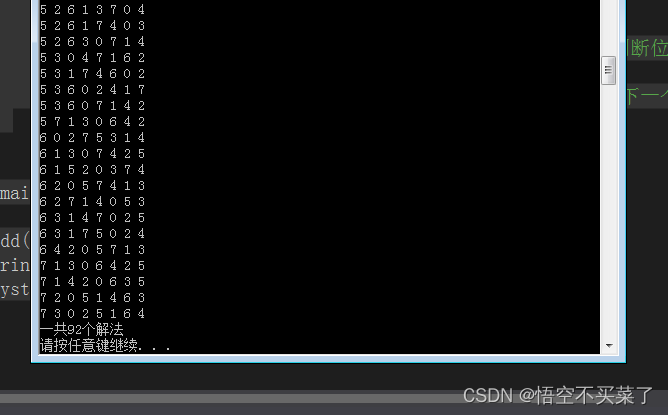
下面来说迷宫问题，这个也是递归回溯的经典问题：

简单说，就是一个小球怎么从一个位置走到另外一个位置。

思路：

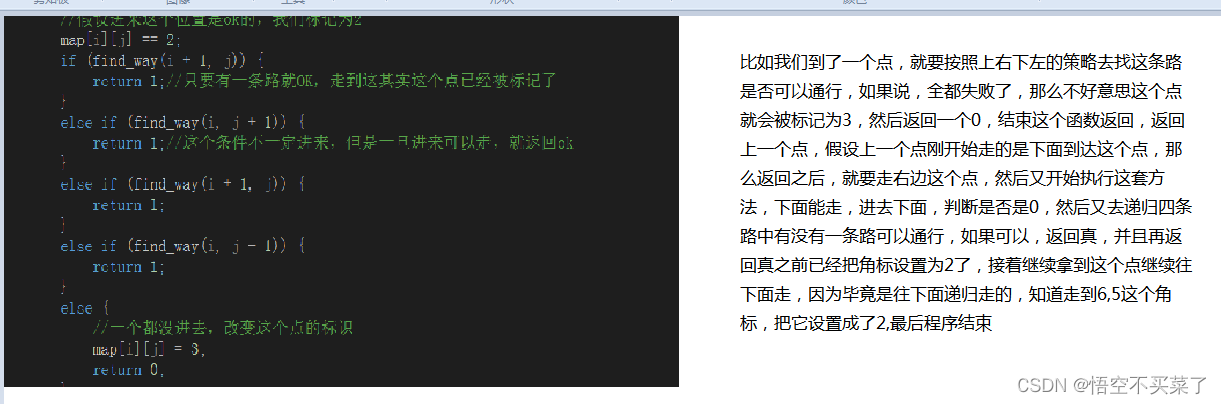
 代码

       

#include <stdio.h>
#include <stdlib.h>static int map[8][7] = { 0 };void print_map()
{//输出这个地图for (int i = 0; i < 8; i++) {for (int j = 0; j < 7; j++) {printf("%d ", map[i][j]);}//每打印一排数据换行printf("\n");}
}//先来创建一个迷宫
//利用二维数组来模拟的迷宫
//墙体全部用数字1表示
void create_maze()
{//使用1表示墙体//上下全部设置为1for (int i = 0; i < 7; i++) {map[0][i] = 1;map[7][i] = 1;}//左右墙体全部设置为1for (int i = 1; i < 7; i++) {map[i][0] = 1;map[i][6] = 1;}//在迷宫里面设置墙体挡板map[3][1] = 1;map[3][2] = 1;
}//开始找路
//i与j代表其实位置，策略就是按照下->右->上->左这个顺序来找路,如果这个点可以通行
//把这个点标记为2
//这个就是下面走不动，走右边，右边不行，走上边，然后在走左边，全都不行，标记3不能通过
int find_way(int i, int j)
{if (map[6][5] == 2) {//最后一个位置return 1;}else {//最关键的一个条件是map[i][j] == 0if (map[i][j] == 0){//假设进来这个位置是ok的，我们标记为2map[i][j] = 2;if (find_way(i + 1, j)) {return 1;//只要有一条路就OK，走到这其实这个点已经被标记了}else if (find_way(i, j + 1)) {return 1;//这个条件不一定进来，但是一旦进来可以走，就返回ok}else if (find_way(i - 1, j)) {return 1;}else if (find_way(i, j - 1)) {return 1;}else {//一个都没进去，改变这个点的标识map[i][j] = 3;return 0;}}else{//这个位置都不对return 0;}	}
}int main()
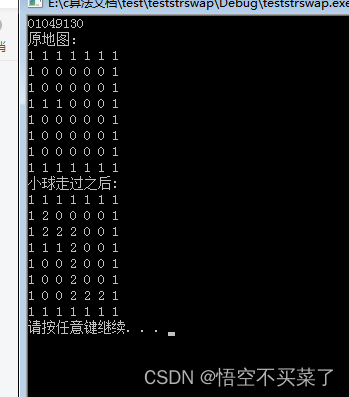
{printf("%p\n", map);create_maze();printf("原地图：\n");print_map();find_way(1, 1);printf("小球走过之后:\n");print_map();system("pause");return 0;
}

 运行结果：