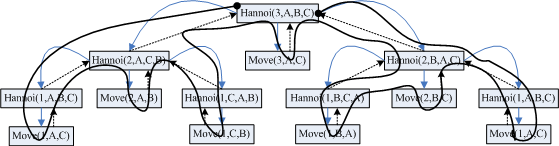
汉诺塔问题：

     

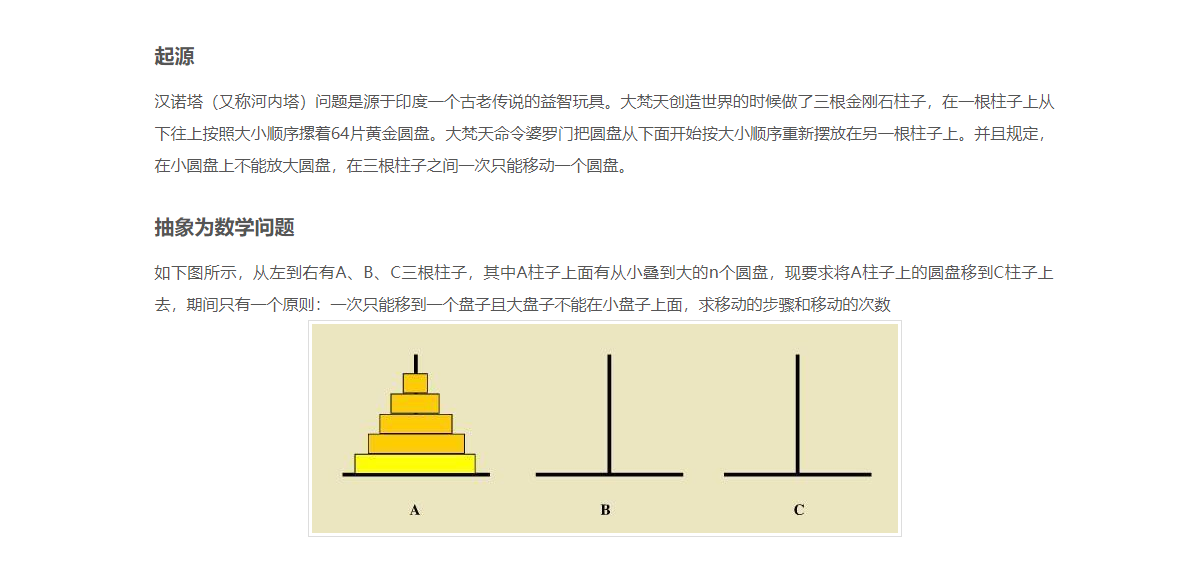
       如果求解的汉诺塔是3层，可以先将上面的两层看作是一个整体。先将两层经过c作为中介移动到b，再将第三个圆盘直接移动到c。然后再将b上面的两个圆盘移动到c，通过a为中介。

算法分析（递归算法）

我们在利用计算机求汉诺塔问题时，必不可少的一步是对整个实现求解进行算法分析。到目前为止，求解汉诺塔问题最简单的算法还是同过递归来求，至于是什么是递归，递归实现的机制是什么，我们说的简单点就是自己是一个方法或者说是函数，但是在自己这个函数里有调用自己这个函数的语句，而这个调用怎么才能调用结束呢？，这里还必须有一个结束点，或者具体的说是在调用到某一次后函数能返回一个确定的值，接着倒数第二个就能返回一个确定的值，一直到第一次调用的这个函数能返回一个确定的值。
实现这个算法可以简单分为三个步骤：

（1） 把n-1个盘子由A 移到 B；
（2） 把第n个盘子由 A移到 C；
（3） 把n-1个盘子由B 移到 C；

从这里入手，在加上上面数学问题解法的分析，我们不难发现，移到的步数必定为奇数步：

（1）中间的一步是把最大的一个盘子由A移到C上去；
（2）中间一步之上可以看成把A上n-1个盘子通过借助辅助塔（C塔）移到了B上，
（3）中间一步之下可以看成把B上n-1个盘子通过借助辅助塔（A塔）移到了C上；

代码实现：

      

public class Hanoi {/***** @param num: 盘子的编号* @param from：盘子的起始时所在的塔的编号* @param inter：盘子通过的中介塔的编号* @param to：盘子最终到达的塔的编号*/public void doHanoi(int num,char from ,char inter,char to ){if (num==1){System.out.println("第 1 个盘子，从"+from+"到--"+to);}else{//将除了最下面的盘子通过to为中介进行移动到interdoHanoi(num-1, from,to , inter);//此时改编号的盘子上方已经没有盘子了，直接将其移动到目标塔System.out.println("第 "+num+" 个盘子，从"+from+"到"+to);//将移动到inter上的盘子经过from到todoHanoi(num-1, inter, from, to);}}public static void main(String[] args) {Hanoi hanoi = new Hanoi();hanoi.doHanoi(3, 'a', 'b', 'c');}
}