2019独角兽企业重金招聘Python工程师标准>>> 
前提说明:
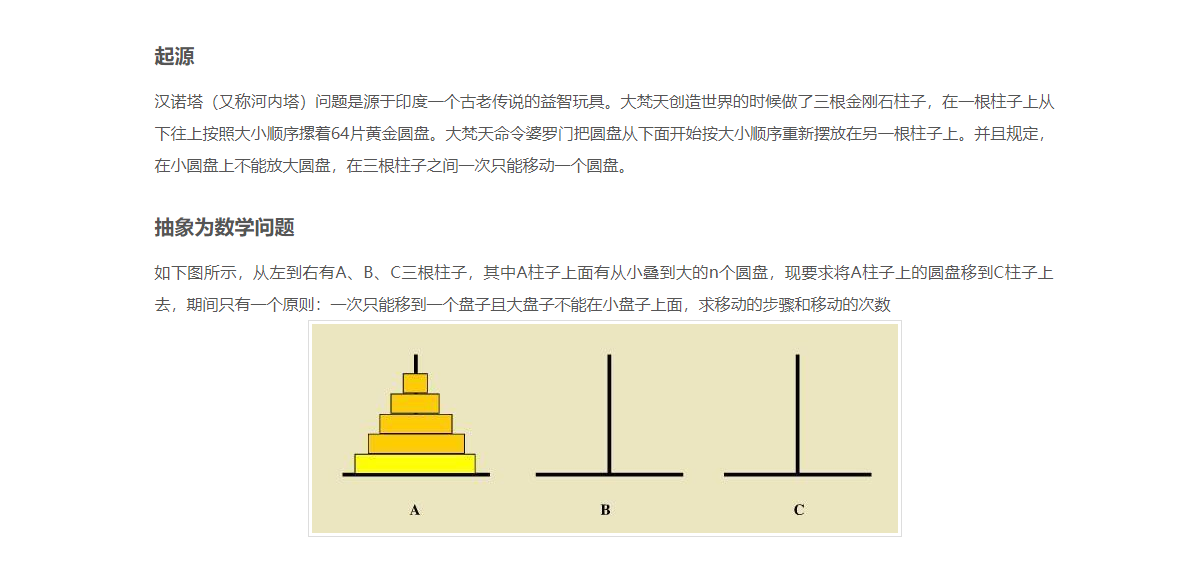
算法:当只有一个盘子的时候,只需要从将A塔上的一个盘子移到C塔上。
当A塔上有两个盘子是,先将A塔上的1号盘子(编号从上到下)移动到B塔上,再将A塔上的2号盘子移动的C塔上,最后将B塔上的小盘子移动到C塔上。
当A塔上有3个盘子时,先将A塔上编号1至2的盘子(共2个)移动到B塔上(需借助C塔),然后将A塔上的3号最大的盘子移动到C塔,最后将B塔上的两个盘子借助A塔移动到C塔上。
当A塔上有n个盘子是,先将A塔上编号1至n-1的盘子(共n-1个)移动到B塔上(借助C塔),然后将A塔上最大的n号盘子移动到C塔上,最后将B塔上的n-1个盘子借助A塔移动到C塔上。
综上所述,除了只有一个盘子时不需要借助其他塔外,其余情况均一样(只是事件的复杂程度不一样)。
上代码:
package mainimport ("fmt"
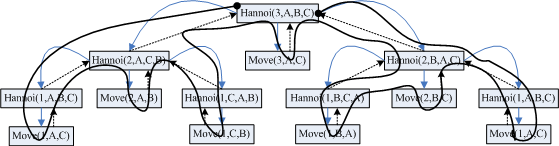
)var count = 0func main() {hanoi(3, "a", "b", "c")fmt.Printf("total move %d times\n", count) //数学归纳法告诉我们count=2^n-1
}func hanoi(n int, one string, two string, three string) {if n == 1 {move(one, three)} else {hanoi(n-1, one, three, two) //首先将n-1个从A经过C移到B上,此时A上剩最大的一个积木move(one, three) //将最大的积木从A移到C上,打印A->Chanoi(n-1, two, one, three) //之后将n-1个从B经过A移到C上,完成}
}func move(a string, b string) {//fmt.Printf("move %s to %s\n", a, b)count++
}原理:就是递归堆栈去做一些重复性的事情,我们只要找出规律,剩下来就靠递归了