递归-斐波那契数列

这里我们讲解一下 斐波那契数列的经典递归问题。
斐波那契数列：
1 1 2 3 5 8 13 21 34…
从第三个数字开始，下一个数字等于前面两个数字之后，有点像我们数学的数列 n(x-1)+n(x-2)
那如果我们要求第n个数字，应该是多少呢？我们的思路是一样的，假设我求n，那第n个数字就等于(n-1)+(n-2)
这里我们用递归的方式来解决。
递归的核心思想就是把大事化小！递归的每一层的功能都是一样！当然我们在采用递归之前，必须清楚我们递归结束

#include <stdio.h>
int fibonacci(int n)
{if(n<=2)return  1;else return fibonacci(n-1)+fibonacci(n-2);
}
int main()
{int input=0;printf("请输入第几个值>:");scanf("%d",&input);int ret=fibonacci(input);printf("第%d个数字为%d\n",input,ret);
}

这样斐波那契数列递归的方式就实现了，但是会发现如果我输入一个50，这样稍微大一点的数字，它的处理速度就会很慢，这是因为，假设我们输入50
fib(50)=
48+49
(47+46)+(48+47)
(46+45)+(45+44)+(47+46)+(46+45)
这样我们就会发现下面的展开就会极其繁琐，虽然斐波那契数列很适合递归，但是递归的效率并不是很高，比较耗费时间，因此为了提高斐波那契数列的效率，我们可以采用循环的方式来解决。

#include <stdio.h>
int fibonacci(int n)
{int a = 1,b = 1,c = 1; //这里C定义为1 是当n为1和2的情况while (n > 2){c = a + b;a = b;b = c;n--;}return c;
}
int main()
{int input=0;printf("请输入第几个值>:");scanf("%d",&input);int ret=fibonacci(input);printf("第%d个数字为%d\n",input,ret);
}

这样虽然我们采用循环的代码没有递归简洁，但是执行效率却会高出很多！

递归-求字符串长度

我们常用的求字符串长度的函数为 strlen(),那我们用递归如何实现呢？

#include <stdio.h>
int my_strlen(char* p)
{if( *p != '\0')return 1+my_strlen(p+1);elsereturn 0;
}int main()
{char arr[]="cynthia!";int ret=my_strlen(arr);printf("字符串长度为 %d\n",ret);return 0;
}

这里需要注意的是，数组在传参的时候，传的是首地址，因此我们需要定义指针变量p来接受地址，在进行递归操作的时候，这要可以选择p+1 或者 ++p，但是不能p++，因为这里如果写p++，就会导致 先把p传给下一次调用，然后再+1，这样就会造成死循环，而导致栈溢出，因此这一点需要格外的注意！

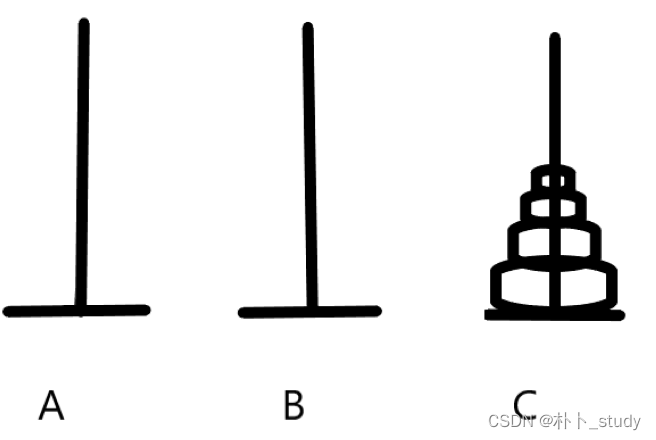
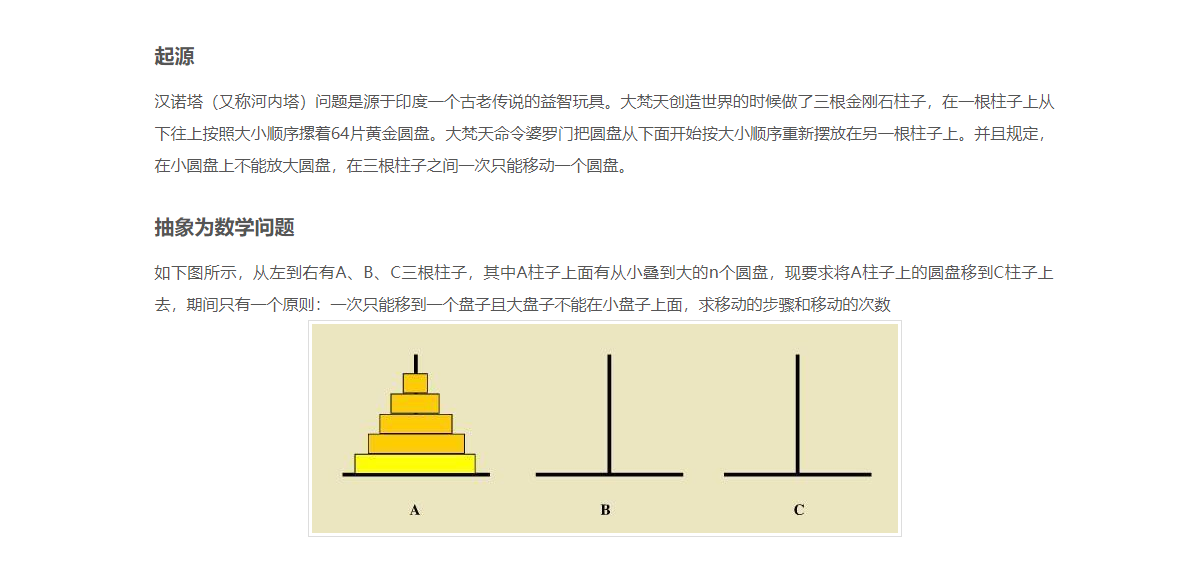
递归-汉诺塔问题

如图所示，我们一共有三根柱子，假设我们现在有3个方块，要求每个柱子上都必须满足小的方块在上，大的在下面的要求，请问3个方块，我们应该怎么操作？
采用递归的思想，大事化小，那我们就把3块分成(3-1)块和1块。
第一步：将（n-1）块放在B上。
第二步：将最后一块放在C上。
第三步：将（n-1）块放在C上。

就相当于我们把上面的n-1块，放在b上面，把最下面的一块放到C，这样层层剥离，我们就可以得到最最终的结果，按照这样的思路，只要方块个数大于一，我们都可以按照三步走的解决思路。
下面我们用代码详细讲解！（正确代码）

#include <stdio.h>
int count=0;
void move(int n,char x,char y)
{printf("%c.%d--->%c\n",x,n,y);count++;
}
int tower(int n,char one,char two,char three)
{if(n==1)move(n,one,three);else{tower(n-1,one,three,two);  //第一步move(n,one,three);         //第二步tower(n-1,two,one,three);  //第三步}return count;
}int main()
{int input=0;printf("请输入方块数量>:");scanf("%d",&input);int ret=tower(input,'A','B','C');printf("一共需要%d次\n",ret);return 0;
}

假设我们只有一个方块，我们只需要将A.1放在C即可。

假设我们有两个方块，那我们就首先需要将第一块方块放在B，然后把最下面的方块放在C，然后再把刚才的方块放回C。
这里解释两个地方：
第一为什么需要 ‘A’,‘B’,'C’这三个字符？
这里我们把ABC当做三个木桩，需要调用ABC来确定把木块放在哪个木桩上。
第二既然这样那我也可以把这三个字符，直接放在tower函数里面，岂不是函数传递的参数更少了？
想法很美好，现实很残酷，首先我们在函数接口中添加这三个变量的目的就是为了后续分辨木桩，如果我把参数放在函数里面，这样我就无法实现动态递归，比如(错误示范)：

int tower(int n)
{char one = 'A', two = 'B', three = 'C';if (n == 1)move(n, one, three);else{tower(n - 1);move(n, one, three);tower(n - 1);}return count;
}

这样就会导致我们无法只用一个move来进行木块转移，而是需要将每一次的输入方块的传递方和接收方，因此这里我们还是采用在函数的接口添加相应的变量，从而达到递归的目的！
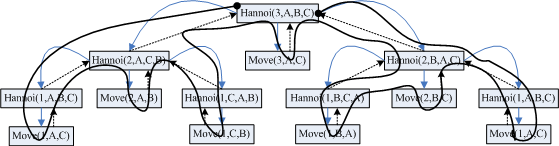
或许大家还有另一个疑惑，那为什么在递归的时候，要写两边tower呢？里面的顺序不同又代表什么意思呢？

第一个递归中
在上面我们讲过了，如果我有n个方块，那我先把(n-1)块放在B，然后再把最后一个放在C，这里就是我们对(n-1)快的操作，至于为什么中间是three，是因为我们最终是要把(n-1)块放在中间桥梁块B上，因此我们(n-1)的最终目标块就是two。当我们执行完(n-1)块后，就可以把最后一块放在C上了，也就是move对应的命令。
第二个递归中
当操作完前两个指令后，我们的第一个工作才算完成，下面才是我们严格意义上的递归，把剩下的方块继续按照之前的步骤重复操作，这里第一个递归是为了将(n-1)块严格按照上小下大的标准进行转移，而第二个递归就是不断的对剩余的方块进行重复的操作，那为什么第二个递归的传递方是two呢，因为经过上面的转移后，剩下的方块都已经被放到了第二个木桩上，因此B就成为了我们的传递方而C依然使我们的接收方。这样我们的递归就全部完成了，下面看看最终效果。

如果有说的有问题的地方，请指正，仅个人观点和看法，如果还有不懂的小伙伴，在评论区留言，看到后会及时回复。

递归-青蛙跳台阶问题

有一个青蛙，一次可以跳一个台阶，也可以跳两个台阶，试问如果要跳n个台阶有多少种跳法。
假设:
有1个台阶：[1] —>1种情况
有2个台阶：[1,1],[2] —>2种情况
有3个台阶：[1,1,1],[2,1],[1,2] —>3种情况
有4个台阶：[1,1,1,1],[2,1,1],[1,2,1],[1,1,2],[2,2] —>5种情况
根据总结出来的规律，不难发现 n=(n-1)+(n-2),和斐波那契数列很相似。
下面我们用代码实践。

#include <stdio.h>
int steps(int n)
{if(n>2)return steps(n-1)+steps(n-2);else if(n==2)return 2;else if(n==1)return 1;elsereturn 0;
}
int main()
{int input=0;printf("请输入台阶数量>:");scanf("%d",&input);int ret=steps(input);printf("一共有%d种情况\n",ret);return 0;
}