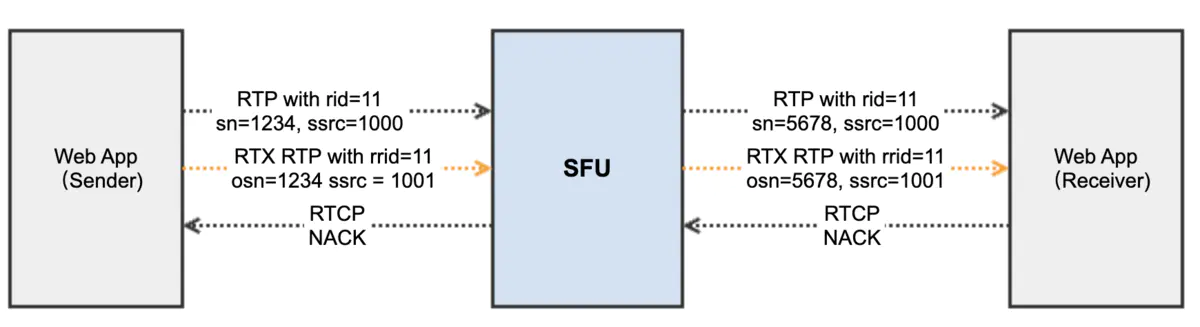
分治算法就是分成若干个和原问题一样性质的子问题，然后逐步递归这些子问题，直到遇到规模很小的子问题，求出子问题的解，归结成原问题的解的算法就是分治算法
分治算法为递归问题，可以用来解决快排、二分归并、斐波那契数列、锦标赛问题、凸包问题等

      递归方程主要分为两类：（1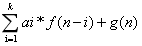）（2）f(n)=af(n/b)+d(n)
      第一种的方程可以用迭代或者递归树求解，如汉诺塔；第二种的方程可以用迭代、递归树、主定理求解，如二分归并排序
      本篇主要介绍分支算法的推导方程的解，即主定理、递归树，以及幂乘运算及其优化、汉诺塔问题

1、递归树

什么是递归树

      递归树是迭代过程的一种图像表述。递归树往往被用于求解递归方程， 它的求解表示比一般的迭代会更加的简洁与清晰。
      递归树有如下概念：
1、递归树是迭代计算的模型。
2、递归树的生成过程与迭代过程一致。
3、递归树上所有项恰好是迭代之后产生和式中的项。
4、对递归树上的项求和就是迭代后方程的解。

递归树的生成

T(n)是原问题的解，我们把T(n)写成T(n)=T(m1)+T(m2)+…+T(mt)+f(m1)+f(m2)+…+f(mt)      在这里前面由T写成的方程是递归子问题，而后面由f写成的是归结子问题解的操作。

这里我们把T写成的式子称为函数项，把f写成的式子成为非函数项

对于T(n)是原问题的解。我们可以把非函数项写成根，把函数项写成叶子，如图：

左边的原问题可以写成右边的递归树，右边的递归树根是非函数部分，也就是归结子问题解的部分，而叶子是函数部分，也就是划分子问题的部分，然后我们发现，这棵递归树所有节点的和就是左边原问题的解，这是第一步迭代的过程。

举个例子：我们在上一篇提到过二分归并排序的算法是T(n)=2T(n/2)+n，这里我们看到，T(n)是原问题的解，而2T(n/2)是函数部分，n是非函数部分。我们可以把2T(n/2)画成叶节点，把n画成根节点。做出迭代两步迭代的递归树：

那么我们可以得出递归树的生成规则：
1、初始：递归树只有根结点，其值为T(n)
2、不断继续下述过程：
将函数项叶结点的迭代式T(m)表示成二层子树
用该子树替换该页结点
3、继续递归树的生成，直至树中无函数项（只有初值）为止。

我们参考上边的继续将二分归并的递归树画出来：

我们发现右边的n是左边节点的和，所以原问题的解=所有节点的和=将右边的n全部加起来就可以了
这是一棵完全二叉树，我们知道完全二叉树的深度是logn,那么logn个n相乘不就是nlogn嘛。所以我们得出二分归并排序的时间复杂度是O(nlogn)。

递归树的应用

接下来，我们通过递归树来分析一个递归方程：
T(n)=2T(n/2)+nlogn （n/2 log(n/2)=n/2(logn-log2)=n/2(logn-1)）
作图，得：

根据完全二叉树定理，n=2^k，即k=logn(n是节点数，k是深度)
将上图右边的式子相加得，
nlogn+n(logn-1)+n(logn-2)+…+n(logn-k+1)
= nlogn+nlogn+nlogn+…+nlogn-n(1+2+3+4+…+k-1)
= nklogn(有多少深度，就有多少的logn。绝对不是n个logn) -n(k(k-1)/2)
= nklogn-n((k^2-k)/2
这里我们把k=logn带进去得，
= n(logn)²-n((logn)²/2-(logn)/2)
= n(logn)²-n(logn)²/2-n(logn)/2
= O(n(logn)²) (读作：logn的平方乘以n)

递归树分的叉数还是要看递归的规模是多少。如果是T(n)=3T(n/2)+n-1或者T(n)=T(n/9)+T(4n/9)+T(4n/9)+n,那就是要分三个叉了

这是用递归树来解这些递归方程

2、主定理

什么是主定理

主定理就是在涉及f(n)=af(n/b)+d(n)递推方程时，可以更快的运用主定理直接求解，不用繁琐计算

在f(n)=af(n/b)+d(n)中
a 是规约后的子问题的个数
n/b 是规约后子问题的规模
d(n) 是规约过程及组合子问题的解的工作量

首先我得说清楚O是上界，比如说f(n)=n²+n,我们就说f(n)=O(n^2),像这样f(n)=O(g(n))，f(n)的阶不高于g(n)的阶
而Ω是下界，比如说f(n)=n²+n,f(n)=Ω(n^2),像这样f(n)=Ω(g(n))，f(n)的阶不低于g(n)的阶
Θ是当f(n)=O(g(n))而且f(n)=Ω(g(n))则记作f(n)=Θ(g(n))。

就能得出这样的解

这里不再证明了，如果感兴趣的话，可以从网上找找证明。这里我们直接应用

主定理的应用

比如，我们要求解二分归并排序的递推方程
T(n)=2T(n/2)+n
这里a=2,b=2,fn=n
根据主定理得，n=n,也就是说f(n)=Θ(n)，那么T(n)=Θ(nlogn)

再比如，T(n)=9T(n/3)+n
这里a=9,b=3,f(n)=n
根据主定理得，n^log3 9=n²,而f(n)=n,我们可以找到一个E=1（主定理1），使得f(n)=O(n),那么T(n)=Θ(n²)
或者说，我们可以根据下面的解来直接得出T(n)=O(n²)

再再比如：T(n)=T(2n/3)+1
这里a=1,b=3/2,f(n)=1
根据主定理得，1=n⁰,即T(n)=Θ(logn)
或者说，我们可以根据下面的解来直接得出T(n)=O(logn)

再看一下，T(n)=3T(n/4)+nlogn
这里a=3,b=4,f(n)=nlogn
根据主定理得，n^(log4 3)约等于n^0.793,那么有E=0.2，使得nlogn=Ω(n^(log4 3))，而且还要使af(n/b)<=cf(n)成立，
则3(n/4)log(n/4)<=cnlogn
3(n/4)(logn-log4)=3(n/4)(logn-2)=3(n/4)logn-3(n/2)
这里我们发现，只要c>=3/4，上述不等式成立。则主定理3成立,即T(n)=Θ(nlogn)
或者说，我们可以根据下面的解来直接得出T(n)=O(nlogn)

当然并不是说所有的递推方程都可以用主定理来解决
大家来看T(n)=2T(n/2)+nlogn
这里a=2,b=2,f(n)=nlogn
首先要知道在都单调递增的情况下，幂函数都是大于对数函数的

你要明白对数函数增长缓慢，而幂函数增长程度是比对数函数要大的多。而指数函数，要比幂函数大的多的多，相比大家听说过指数爆炸吧。如果你的代码量的时间复杂度是个指数函数（比如：2ⁿ），我就这么说,你的数据量如果超过了27。那么你的运行时间就可能会超过1秒。所以说算法就是尽量解决这一类问题，让时间复杂度降一个量

对于时间复杂度的量，就是指数的量>多项式的量>对数的量。你这样的每降一次，那么你的运行效率就会提高不止一个档次。运行时间慢就要考虑你的代码问题，而代码混乱的问题就是代码设计模式的问题，当然设计模式也是可以用来提高性能和效率的，这一点在游戏开发格外重要。所以设计模式+数据结构+算法都是程序员的内功心法

好了我们回到正题，f(n)要等于Ω(n^(1+E))(E>0)。也就是,n·logn=Ω(n·n^E)(E>0)。而且幂函数都是大于对数函数。所以logn<n^E，因此找不到一个E满足那个下界（大于等于那个函数）。因此不成立，所以不满足主定理3。也就不能求解。

而且去用下面的解c是logn，不是常数。所以也解不出来。

那要怎么处理呢，我们可以用递归树解这个递归方程，求解在上面递归树那里有，我已经写出来了。

主定理就是解决求递归方程解的问题的，当然要根据情况进行求解。

3、幂乘算法及其优化

什么是幂乘算法？

很简单，就是求n^x次方，例如求2⁵。2⁵=32

我们先来看普通的幂乘算法

普通幂乘算法

幂乘算法，我记得学循环的时候，不就接触了这个东西了嘛。你用for写，用while写，不都可以。都是很简单的东西，包括递归

比如啊，你要求aⁿ，那么你要传入a,n到函数(方法)里面，用for就是n- -，n>=1,或者啊，就是i=0,i<n,i++。反正方法体里面都是 res*=a(res就是结果)。

对于递归就是n为0，返回1，n为1，返回本身，其他的就返回a*pow(a,n-1)，一直递归，找到出口，然后将值一步步返回

不多说了，直接上代码

public static void main(String[] args) {Random random=new Random();int a=random.nextInt(15);int r=random.nextInt(10);System.out.println("计算"+a+"的"+r+"次方的值");int res=pow(a, r);System.out.println("结果是："+res);}//简单幂乘(迭代写法)public static int pow(int a,int r) {int res=1;for(int i=0;i<r;i++) {res*=a;}return res;}//简单幂乘(递归写法)public static int pow2(int a,int r) {if(r==0)return 1;else if(r==1)return a;else {return a*pow2(a,r-1);}}

简单幂乘算法分析

顺序相乘，实则就是n从1到n本身，总共n个数。那么时间复杂度就是O(n)

如果我们还有优化，那就是要优化到O(logn)，下面我们来看一下优化的幂乘算法。

快速幂算法

我们考虑用分治法进行划分

当n为偶数时，可以划成n/2个a和n/2个a相乘。这两个是均匀划分的子问题，而且对于这两个n/2个a，既然你都算出来了n/2个a是多少了，那么对于右面我们就不必再计算了，只做一个子问题的计算就行了，右面的直接拿来用就行了。就因为这样减少了一半的时间。就这样递归下去。

当n为奇数时，我们可以划分成2个(n-1)/2个的a的子问题相乘，然后再和a相乘。也就是
(n-1)/2个a与(n-1)/2个a与a相乘(大家要多思考，多想想)。这样也是近似减半的算法，也差不多减少了一半的时间。就这样递归下去。

我们分析下不管奇数还是偶数，我们都可以用(a,n/2)来进行递归,此时，n为1,就返回本身。否则继续递归。

我们在n=1的时候找到了res=a之后向上返回之后，（在n-1次递归的时候的n要不是2，要不是3。大家可以想想是不是），好我们继续思考，然后进入n的奇偶判断

我们根据上面的图不难想到，如果是偶数，那么就是res乘以res，如果是奇数那么就是res乘以res乘以a

好，我们来看下代码

public static void main(String[] args) {Random random=new Random();int a=random.nextInt(15);int r=random.nextInt(10);System.out.println("计算"+a+"的"+r+"次方的值");int res=pow3(a, r);System.out.println("结果是："+res3);}//快速幂算法public static int pow3(int a,int r) {int res=1;if(r==0)return 1;else if(r==1)return a;else res=pow3(a, r>>1);if(r%2==0)return res*res;  //如果r为偶数，则乘其本身elsereturn res*res*a;  //如果r为奇数，则乘其本身和a}

快速幂算法的分析

首先，递归肯定是T(n/2),然后乘以res和乘以a，都是一步计算，我们都可以想成O(1)的量。因此T(n)=T(n/2)+O(1)
用主定理分析解出时间复杂度就是O(logn)。

快速幂算法下，有一个重要的应用叫作斐波那契数列。我们再下一篇（分治算法的改进和矩阵（斐波那契数列和Strassen矩阵）下的分治算法）中去说

4、汉诺塔问题

什么是汉诺塔问题

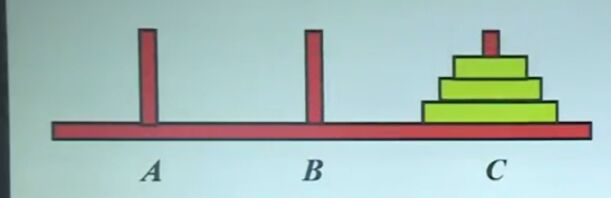
汉诺塔（又称河内塔）问题是源于印度一个古老传说的益智玩具。大梵天创造世界的时候做了三根金刚石柱子，在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定，在小圆盘上不能放大圆盘，在三根柱子之间一次只能移动一个圆盘。

抽象成数学问题就是
如下图所示，从左到右有A、B、C三根柱子，其中A柱子上面有从小叠到大的n个圆盘，现要求将A柱子上的圆盘移到C柱子上去，期间只有一个原则：一次只能移到一个盘子且大盘子不能在小盘子上面，求移动的步骤

移动的步骤就是这样的

                                     

对于汉诺塔问题，就是这样分析

对于三个盘子的情况是这样的：

我们先把n-1个盘子放到B处

然后把底下那个最大的盘子放到目标位置处

最后将那个n-1个盘子放到目标位置处

ok，移完了

对于那个什么n-1个盘子怎么移过去的，我不管。

而且代码也可以这么写。先放伪码

大家可以想想刚才的步骤，再看看伪码。你会豁然开朗的。

对于内部那些操作交由递归来实现就行了。

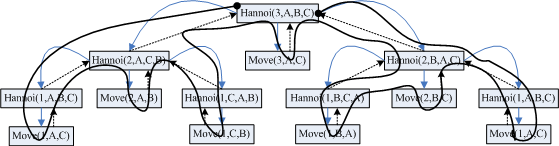
然而我们可以分析得出
（1）中间的一步是把最大的一个盘子由A移到C上去；
（2）中间一步之上可以看成把A上n-1个盘子通过借助辅助塔（C塔）移到了B上，
（3）中间一步之下可以看成把B上n-1个盘子通过借助辅助塔（A塔）移到了C上；

对于内部递归是怎么操作的，大家可以自己动手分析下，这里就放个图

好，我们上代码

public static void main(String[] args) {// TODO Auto-generated method stubint n=3;  //共有3层char a='A';  //A是出发点char b='B';  //B是暂存点char c='C';  //C是终点Hanoi(n, a, b, c);}public static void Hanoi(int n,char A,char B, char C) {if(n==1) Move(A,C); //将出发点移动到终点else {Hanoi(n-1, A, C, B);  //将n-1个塔从出发点移动到暂存点，其中以终点为辅助Move(A, C);Hanoi(n-1, B, A, C);  //将n-1个塔从暂存点移动到终点，其中以出发点为辅助}}public static void Move(char from,char to) {System.out.println(from+"——>"+to);}

把n调调，既可以实现3个，也可以实现4个。

汉诺塔算法的分析

两个递归而且都是从n-1开始的，所以是2T(n-1)。对于从A移动到C是1步，那么就是
T(n)=2T(n-1)+1
T(1)=1
求解这个方程的思路是
T(n)+1=2(T(n-1)+1)
T(n)+1/(T(n-1)+1)=2
也就是T(n)+1是初值为2，公比为2的等比数列
因此得出T(n)=2^n
所以汉诺塔的时间复杂度是O(2^n)，居然是个指数级，那么我们要思考有没有一个优化来降低这个时间复杂度。

目前的答案是：没有，不存在一个多项式时间的算法。

        靡不有初，鲜克有终《诗经·大雅·荡》