一、汉诺塔问题

      1.汉诺塔问题

       起源：一位法国数学家曾编写过一个印度的古老传说：在世界中心贝拿勒斯的圣庙里，一块黄铜板上插着三根宝石针。印度教的主神梵天在创造世界的时候，在其中一根针上从上到下地穿好了由大到小的64片今片，这就是所谓的汉诺塔。不论白天黑夜，总有一个僧侣在按照下面的法则移动这些今片：一次只移动一片，不管在哪根针上，小片必须在大片上面。僧侣们预言，当所有的金片都从梵天穿好的那根针上移到另外一根针上时，世界就将在一声霹雳中消失，而梵塔、庙宇和众生也都将同归于尽。

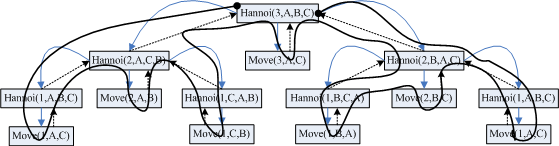
      我们可以将上面问题抽象为，将放X上的64个盘子，按照从小大到的顺序挪到Z上，并且可以借助Y，如图所示：

     

      2.问题分析

      这其实是一个经典的递归问题。

      我们可以这样思考：

• 先将前63个盘子移动到Y上，确保大盘在小盘下；
• 再将最底下的第64个盘子移动到Z上；
• 最后将Y上的63个盘子移动到Z上。
• 这样子看上去问题就简单了一点，但是关键在于第1步和第3步应该如何执行呢？

      通过研究发现：

      (1)每次移动一个圆盘，在移动过程中必须要借助另外一根针才能完成；

      (2)也就是说第1步将1~63个盘子借助Z移动到Y上，第3步将Y针上的63个盘子借助X移动到Z针上，那么我们将思路聚集在以 下两个问题：

• 问题一：将X上的63个盘子借助Z移到Y上；
• 问题二：将Y上的63个盘子借助X移到Z上。

      问题一的圆盘移动步骤为：

• 先将前63个盘子移动到Z上，确保大盘在小盘上；
• 再将最底下的第63个盘子移动到Y上；
• 最后将Z上的62个盘子移动到Y上；

      问题二的圆盘移动步骤为：

• 先将前62个盘子移动到X上，确保大盘在小盘上；
• 再将最底下的第63个盘子移动到Z上；
• 最后将X上的62个盘子移动到Y上；

       3.代码实现

#include <stdio.h>// 将n个盘子从x借助y移动到z
void move(int n, char x, char y, char z){if(1 == n){printf("%c-->%c\n", x, z);}else{move(n-1, x, z, y); // 将n-1个盘子从x借助z移到y上printf("%c-->%c\n", x, z);move(n-1, y, x, z); // 将n-1个盘子从y借助x移到Z上}
}int main(){int n;printf("请输入汉诺塔的层数：");scanf("%d", &n);printf("移动步骤如下：\n");move(n, 'x', 'y', 'z');return 0;
}

 

本文为原创文章，如果对你有一点点的帮助，别忘了点赞哦！比心！如需转载，请注明出处，谢谢！