细雨灯花落,泪眼若为容。
Open Gapps
GAPPS是谷歌软件服务集合(Google Apps)的缩写形式。由于移动设备生产厂商的某些限制,一些运行Android系统的设备没有安装谷歌服务框架。这类设备在无法运行一些基于谷歌服务框架开发的应用软件及游戏时,需要安装包含谷歌服务框架的谷歌软件服务集合,即GAPPS。
OPEN GAPPS官网下载(需要禾斗学上网)
OpenGApps有几个不同的版本,super、stock、full、mini、micro、nano、pico。
super
包含了所有 GApps ,像韩语日语中文拼音中文注音输入法等。(请注意:如果你是用的是基于原生的 ROM ,本版本会替换相机,通讯录等等所有有关应用)。
stock
类似于 Google Pixel 出厂内置的 GApps ,相比 super 版少了其他语种的输入法以及 Google 地球等。(请注意:如果你是用的是基于原生的 ROM ,本版本会替换相机,通讯录等等所有有关应用)。
full
与 stock 版所包含的内容相同,但此版本不会替换手机原本的应用。
mini
包含基础的 Google 服务框架,以及一些影响力较大的 GApps ,相比 full 版去掉了 Docs 等应用。
micro
包含基础的 Google 服务框架和 Gmail 等常见 GApps。
nano
包含基础的 Google 服务框架,但不会有其他 不必要的 GApps。
pico
包含最迷你的 Google 服务框架,但由于框架并非完整,部分 GApps 可能无法运行。



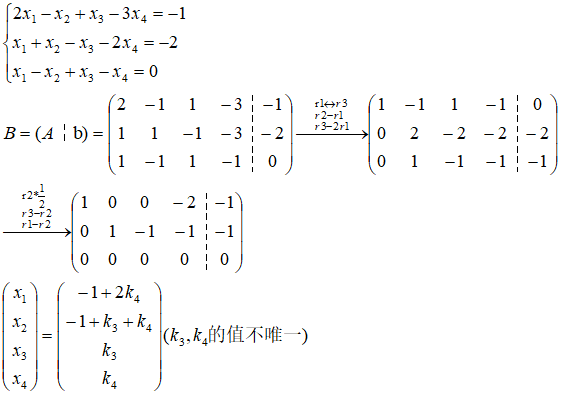






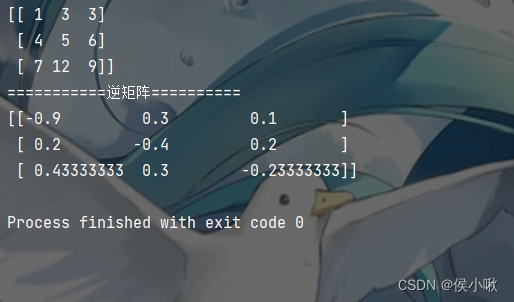






![线性代数[向量]](https://img-blog.csdnimg.cn/35d8c6f2c260420296d2c546a1a08336.png)

