一、矩阵是什么

（1）矩阵的概念

        矩阵就是 m x n 个数排列成 m 行 n 列的表格，其具体形式为：

 （2）矩阵与行列式的区别

        a.  矩阵是一个数表，而行列式只是一个n阶的方阵;

        b.  矩阵的行数和列数可以不同，而行列式行数和列数必须相同。

        c.  矩阵不能从整体上被看成一个数，而行列式最终可以算出来一个结果数值;

        d.  两个矩阵相加（减）是将同位置上的元素相加（减），而两个行列式相加（减）则是单独计算出两个行列式在进行相加（减）；

        e.  用一个数乘以矩阵是指该数乘以矩阵的每一个元素，而用一个数乘行列式，只能用此数乘行列式的某一行或列，提公因数也如此。

二、矩阵的加减

（1）加减法规则

        a.  只有两个矩阵为同型矩阵时才可以进行相加减操作；

        b.  两个矩阵相加减是同位置上的元素进行相加减；

        c.  矩阵相加时 A + B = B + A;         A + ( B + C ) = ( A + B ) + C;        与数的相加减规则几乎一样；

（2）

        例：

有（ A ）、（ B ）两个矩阵，如图所示

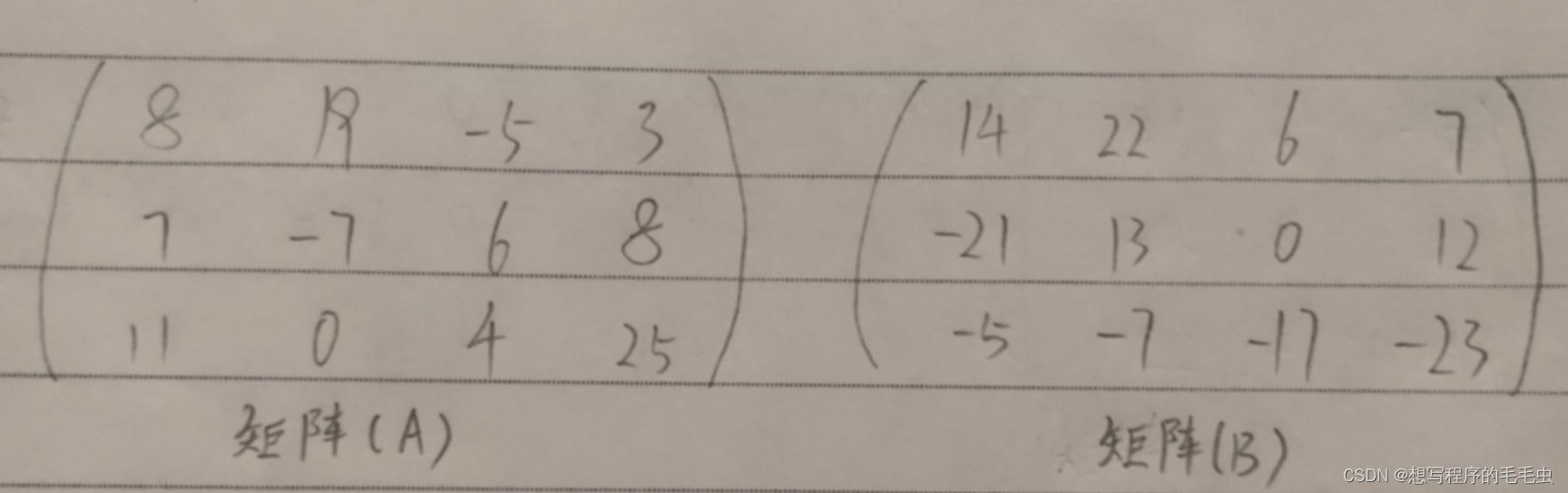
求：（ A ）+（ B ）；

        解：

三、矩阵的相乘

（1）矩阵相乘的规则 

        a.  前行乘后列；

        b.  矩阵相乘不满足交换律，即 A x B ≠  B x A ；

        c.  三个矩阵相乘时 A x B x C ；可以先算 A x B 也可以先算 B x C ；

        

（2）

        例：

有（ A ）、（ B ）两个矩阵，如图所示

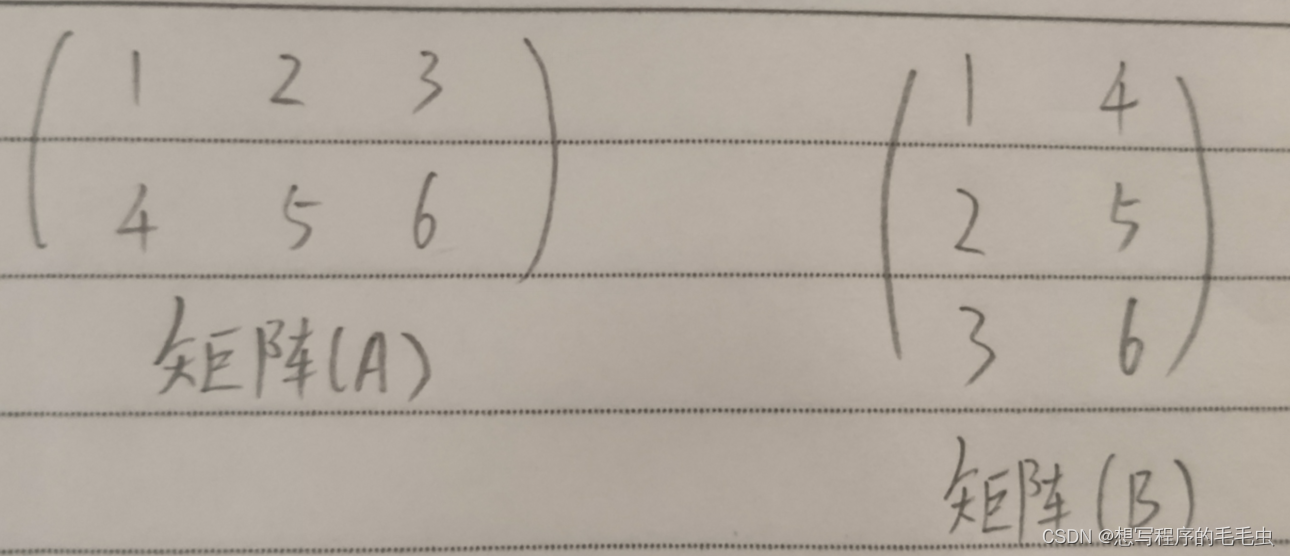
求：（ A ）X（ B ）；

        解：

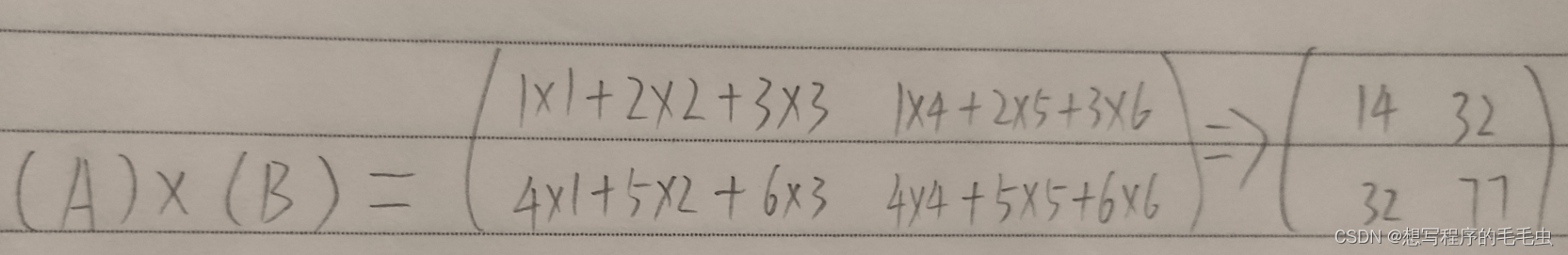
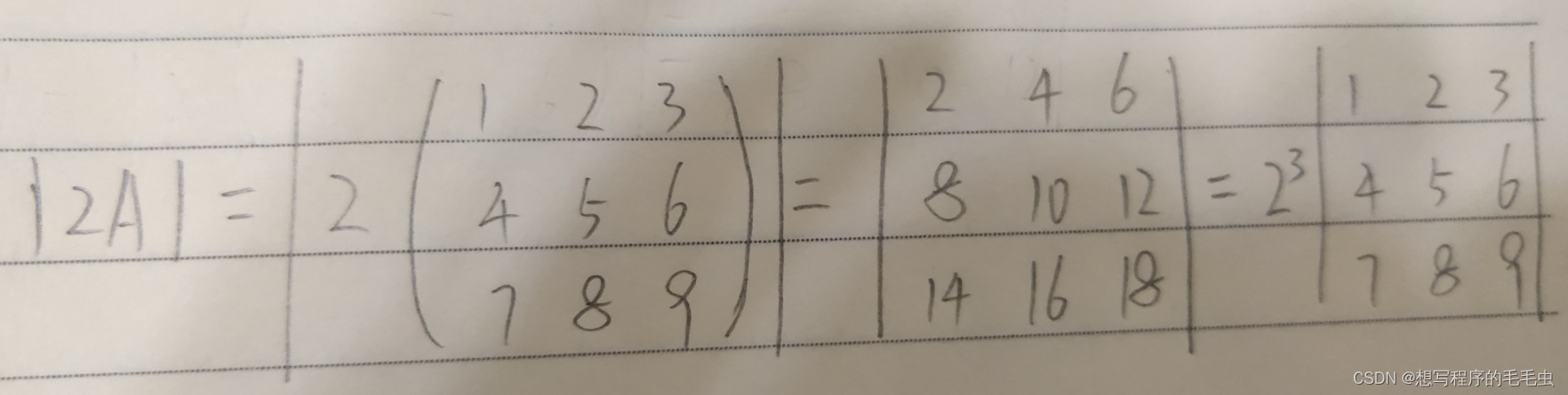
 （3）行列式与矩阵：| aA | = a^n | A |

        例：已知矩阵（ A ），求 | 2A | ；

        解：

 四、转置矩阵

（1）转置矩阵的定义

        转置矩阵就算将一个矩阵的行列调换生成的一个新的矩阵，记作 矩阵^T ；

（2）转置矩阵的规则

        a.  转置矩阵再进行一次转置会变回原来的矩阵；

        b.  两个矩阵相加（减）后转置相当于两个矩阵转置后相加（减）；

        c.  一个数乘以一个矩阵后转置相当于这个数乘以该矩阵的转置矩阵；

        d.  两个矩阵相乘后转置相当于两个矩阵转置后互换位置相乘；

        e.  转置矩阵的行列式的值与原矩阵相同；

（3）

        例：

有（ A ）、（ B ）两个矩阵，如图所示

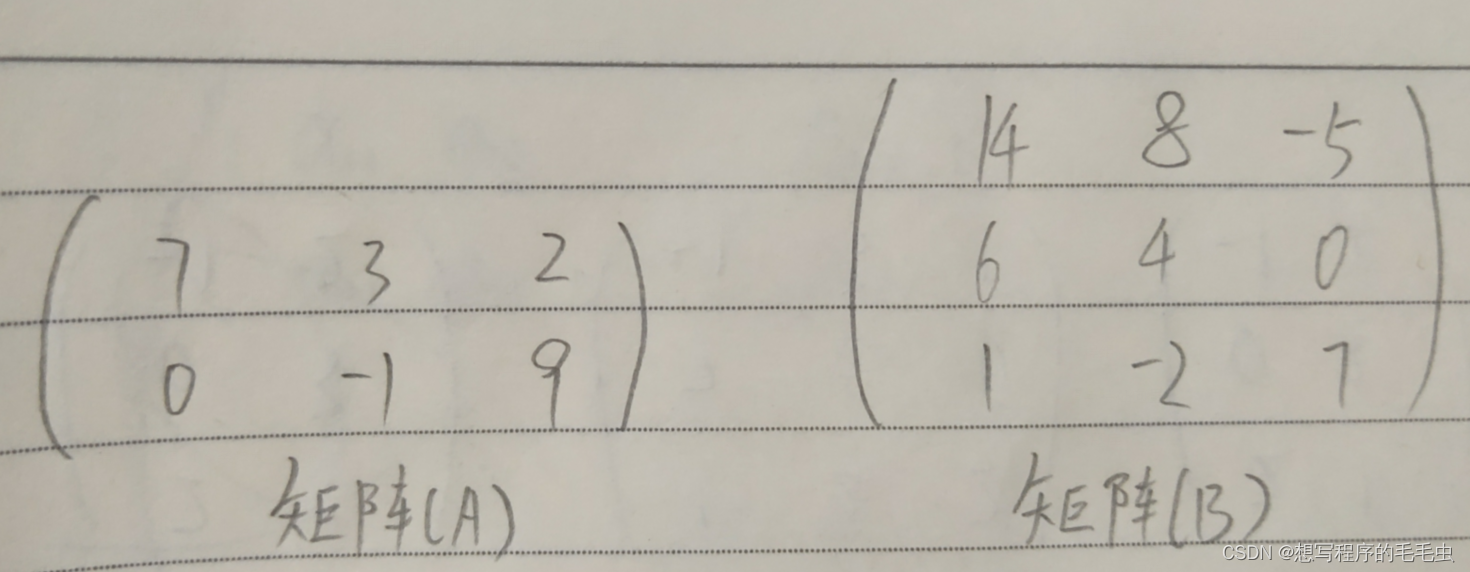
 求：（ AB ）^ T ;

        解：