矩阵（Matrix）是一个按照长方阵列排列的复数或实数集合，矩阵是许多学科中常用的数学工具。

1 矩阵运算

    m*n个数aij(i=1,2,...,m;j=1,2,...,n)排成m行n列的矩形数表：

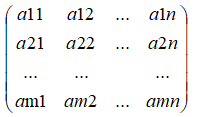
    称为m*n矩阵，一般记为Am*n。

    元素是实数就是实矩阵，元素是复数就是复矩阵。

    当m=1，矩阵A称为行矩阵，也叫n维行向量。

    当n=1，矩阵A称为列矩阵，也叫m维列向量。

    行列式和矩阵的区别是，行列式是一个确定的数和代数式，而一个矩阵仅是一个数表，行列式的行数和列数必须相同，而矩阵的行数和列数可以不同。

    左边称上三角矩阵，右边称下三角矩阵。

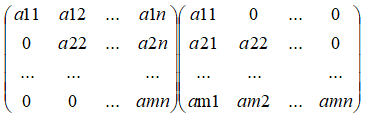
    矩阵加法，C=A+B如下：

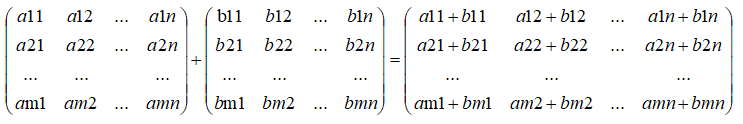
    矩阵数乘，kA如下：

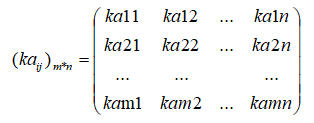
    矩阵的加法与数乘满足以下规律：

(1)A+B=B+A      (2)(A+B)+C=A+(B+C)(3)A+0=A        (4)A-A=0(5)1*A=A        (6)klA=k(lA)(7)k(A+B)=kA+kB (8)(k+l)A=kA+lA

    矩阵乘法C=AB如下：

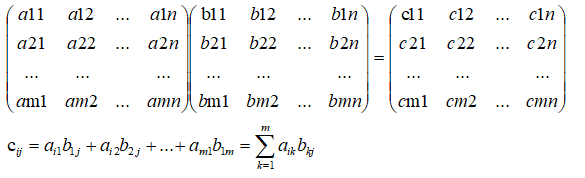
    只有当A的列数等于B的行数，两个矩阵才能相乘，还有以下运算律。​​​​​​​

AB≠BA(AB)C=A(BC)A(B+C)=AB+ACkAB=A(kB)

    如下矩阵，若λ为1则称该矩阵为单位矩阵，否则称数量矩阵。

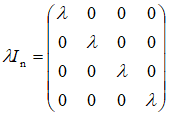
    A的转置矩阵如下：

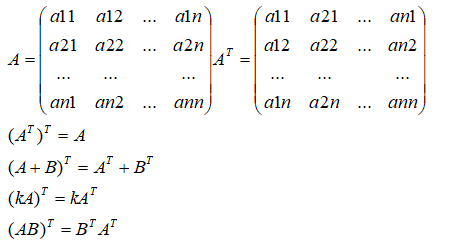
2 矩阵的逆

    n阶矩阵A的行列式记为|A|，有以下性质：

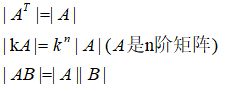
    |A|不等于0则称非奇异矩阵，等于0则称奇异矩阵。

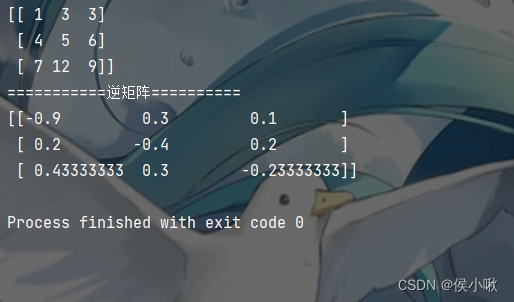
    如过存在下列式子，则称A是可逆的，B是A的逆矩阵，且A的逆矩阵是唯一的。

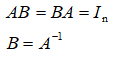
    A的伴随矩阵为A*如下，Aij是A的行列式|A|中元素aij的代数余子式，由此可退出A的逆矩阵。

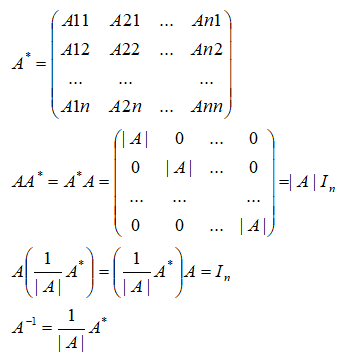
    然后推出逆矩阵的行列式：

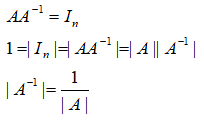
    逆矩阵有以下性质：

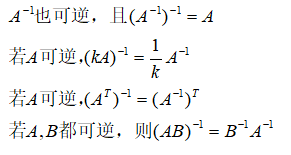
3 矩阵的分块

    对于行列数较高的矩阵A，可以分成许多子块，每一个子块又是一个矩阵。

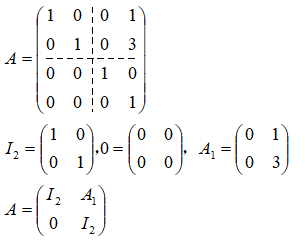
    分块矩阵的运算和矩阵的运算一样，如下例子。

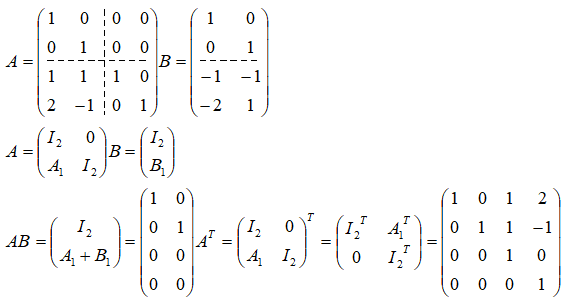
4 矩阵的初等变换与秩

    矩阵的初等变换如下：

• 矩阵i行(列)与j行(列)交换，记为ri↔rj(ci↔cj)

• 矩阵的第i行(列)乘以常数c，记为cri(cci)

• 矩阵的第j行(列)的k倍加到第i行(列)，记为ri+krj(ci+kcj)

    单位矩阵In经过一次初等变换得到的矩阵称为n阶初等矩阵。

    对任何m*n矩阵A作一次初等行变换就相当于在A左边乘上一个相应的m阶初等矩阵；对A作一次初等列变换就相当于在A右边乘上一个相应的n阶初等矩阵。如下例所示：

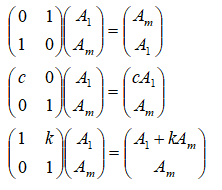
    若矩阵A经过一系列初等变换矩阵变成B，则称矩阵A与B等价，记为A~B

    行阶梯矩阵：(1)如果某行全为0，则该行下方所有行也全为0。(2)如果某行不全为0，且该行第一个不为0的元素所在列的下方所有行也全为0

    行最简矩阵：(1)非0行第一个元素都是1。(2)非0行的第一个非0元素所在列的其余元素全为0

    标准行：任意一个m*n矩阵A都与一个形式如下的矩阵D等价

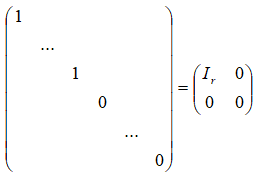
    用一系列初等行变换把可逆矩阵A变成单位矩阵的同时，同样的初等行变换可把单位矩阵变成A的逆，如下所示：

    在矩阵A=(aij)m*n中任取k行k列(1<=k<=m,n)，位于这些行和列相交处的k^2个元素，按照原有的顺序所构成的k阶行列式，称为矩阵A的一个k阶子式。

    A中所有非零子式的最高阶数称为矩阵A的秩，记为(A)，矩阵的初等变换不改变矩阵的秩，如下：

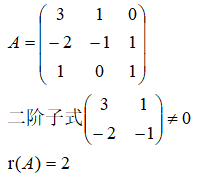
5 高斯消元法

    含m个方程n个未知向量的线性方程组具有以下形式：

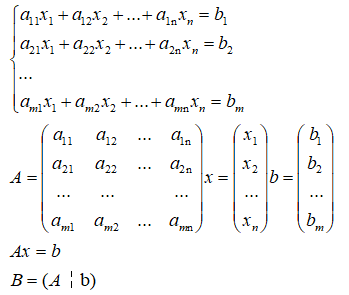
    A称为线性方程组的系数矩阵，B称为线性方程组的增广矩阵

    行列式中是在m=n且行列式值不为0的情况下求解，矩阵可以求m不等于n的解的存在行和解的个数，如下列方程组的求解：

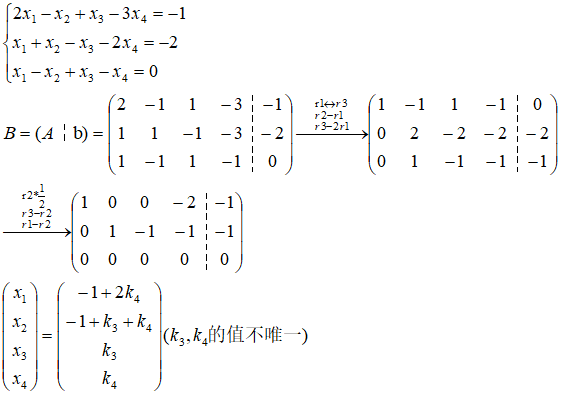
    线性方程组有解的充要条件是系数矩阵的秩与增广矩阵的秩相等r(A)=r(B)

    当r(A)=r(B)=n时，方程组的解唯一

    当r(A)=r(B)=r<n时，方程组的解有无穷多个