写在前面

本文是笔者用于复习本科期间所学线性代数，试图用一种更易接受的方式加强记忆。

从向量到矩阵

线性在何处，矩阵怎么来的

其【线性】体现在经过矩阵的变化后，总是保持网格平行且等间距，因为其仅仅通过拉伸和旋转两个操作来完成，体现在二维空间中有以下两个特征（其最根本的数学特征是【满足加法和数乘两个操作的封闭性】，通俗来说，映射后施加变化 和 施加变换后映射 结果相同）：

• 原点不变
• 直线不弯曲

这样的特征使得张成空间内任意一个向量，比如二维空间中（-1，2），在经过一系列线性变换后，在新的坐标系下仍为（-1，2）。这样n维矩阵的每一列，实际上代表的就是【n个基向量经过各自变化后的目标位置】。如果我们此时拿矩阵对向量做乘法，向量中的每个数隐含的意义是每个原基向量的拉伸程度，也就是向量中现在的每个数将会乘以变化后的基向量。封闭性就是这样体现的。

【总结一下】：一个数是拉伸，二维向量是某个矢量的拉伸和旋转，多个向量的线性组合就是矩阵，是n维矩阵的n个基分别在新坐标系下【保持线性】的拉伸和旋转。我们使用矩阵这种形式来描述高维空间上的变化。

秩，矩阵，逆矩阵

除去上述的直观理解，矩阵最早应用的意义是【解多元方程组】。数学家将复杂的线性表达式的系数单独提出，写成矩阵的形式。

例如下面这个式子，我们【寻找一组系数】使得A的列向量的线性组合等于b（换句话说，我们求解一个向量x，使得经过A这个矩阵的线性变化后构成b），此时通过这n个式子解出的n个未知数使得方程成立。

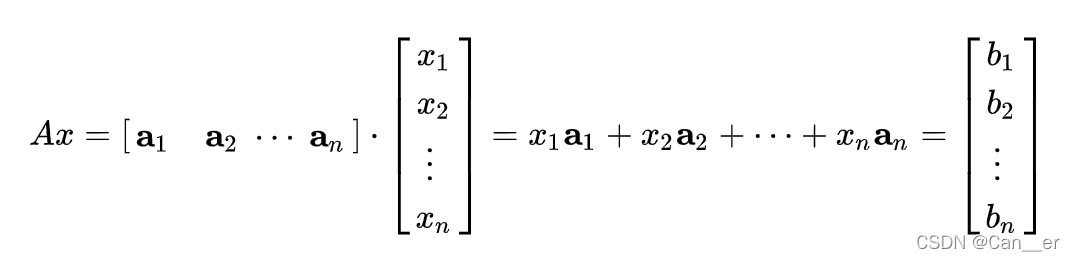
每个矩阵对应的都是对基坐标进行【一组列向量变换】，然后求它们的（向量）和。理解了矩阵实际上是高维空间的线性变化后，就可以引入逆矩阵的概念，逆矩阵是从x到b的变化 $\to$ b到x的变化。譬如一个矩阵是将空间中x拉伸成3倍，并旋转90度，则其逆矩阵就是反向旋转90度，并恢复x。所以 $A^{-1}\dot{A}$ = $A{\dot{A}}^{-1}$ = $E$，也就是什么都不做。
在解方程中，相当于追溯了x到b的变化，使得b通过反向变化，回到x，此时 $x=b{A}^{-1}$ 成功被求解。

而当A并不满足n维时（A不是满秩，线性相关了），意味着降维。【秩意味着经过矩阵变换后空间的维数】。此时其逆矩阵（假设其存在的话）不得不将某个线映射为一个新的面，是我们定义的矩阵乘法中不支持的，或者说升维这个变换无法用矩阵准确描述。这时候需要看b的情况，也就是【线性方程组有解的充要条件是】系数矩阵的秩等于增广矩阵的秩。

注意，【行列式为0并不意味着解不存在】，此时b如果满足在降维后的解空间内，则方程仍然有解。

另外一种描述矩阵可逆的说法是【是多个初等变换的乘积】，因为向量的伸缩，换位和加减并不影响它们的相关性，也就不影响矩阵的秩。所以，可逆矩阵一定可以分解为一系列初等变换，也一定可以通过一系列反向的变换得到单位矩阵。

具体运算

乘法

对于任意输入的向量a, 乘以矩阵A的输出是另外一个向量 b ， 比如：

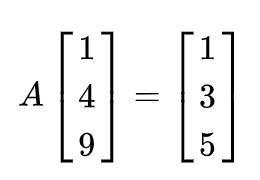
• 从向量的角度来理解：矩阵对该向量施加了空间上的变换，视该列向量在三维空间下，那么矩阵的每一列对应的就是一个原来矩阵中基向量不同维度的拉伸或旋转。乘法使得缩放同等维度的（向量不变）【变化后的基向量】再相加。
• 从矩阵的角度来理解：其本质是以向量a的三个数1,4,9对矩阵中的每一列进行了线性变换，所以乘法本质上是【列向量的线性组合】1，以上面为例是$1\ast a_1$+4*$a_2$+9*$a_3$。

更一般的：

从上述形式中我们可以比较直观的发现，左矩阵控制的是行变换，右矩阵是列变换！ 比如 $a_{11}$ 的改变仅影响第一行。这一点在应用于线性方程组中将会体现的更加明显。

行列式

向量的秩为一维空间拉伸的程度。行列式就是矩阵对应的线性变换对空间的拉伸程度的度量，或者说物体经过变换前后的面积（体积）比。补充一点，这个公式用拉伸的想法来理解就非常容易了：$|AB|=|A||B|$。

• 当一个矩阵的行列式为0时，说明其被降维，此时我们称之为矩阵的【列相关】，也就是n列的矩阵代表的并不是n维的向量空间，而是更少维数，而之所以出现这种现象是由于某些向量可以通过线性组合获得其它向量，也就是存在【本应该单独做一个维度的向量在其它一个或多个向量张成的空间上】。
• 当一个矩阵的行列式为负数时，说明其被翻转，eg在三维空间体现的就是从左手坐标系转换为了右手坐标系。

点乘和叉乘

• 点积：点积是针对同维度向量而言的，其一种直观解释是：投影后，长度相乘。也就是消除了夹角的影响（这个影响反应在了投影）后两个向量的“长度”之积。
  这里3Blue1Brown补充说明了一点：为什么向量点积的意义是投影？想象一个矩阵，使得二维空间压缩至一维，此时我们假设一维上存在一个单位向量，而这个单位向量向x和y轴分别投影的坐标$（u_x,u_y）$，实际上根据对称性，就是 x上的单位向量向u的投影长度 和 y上的单位向量向u的投影长度。也就是这个变化对应的矩阵。任何一个向量施以该矩阵的变化，得到的结果就是新的基向量的重新组合，而新的基向量的坐标就是上面提到的$（u_x,u_y）$。

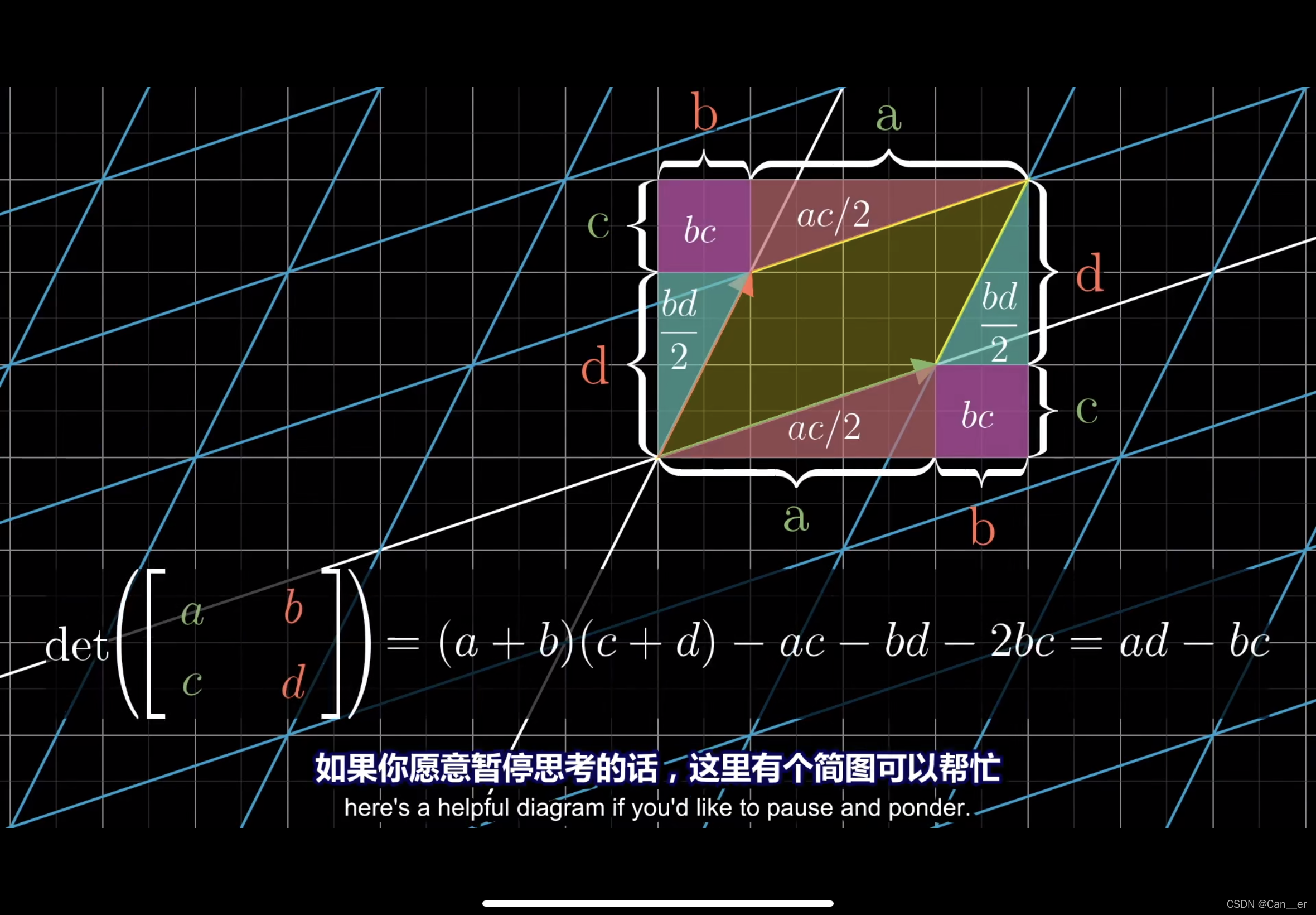
• 叉积：一种经典的记忆方式是叉积代表的是两个向量所形成的平行四边形面积，方向由乘积顺序决定。我们可以将叉积和行列式结合起来记忆，因为行列式的值就是这个平行四边形的面积。所以有以下计算形式：
  
  而其数学上证明存在的意义是，将三维空间中任意一个向量 $(x,y,z)$ 施加点乘，其实是投影到了和v与w形成平面的垂线上，而这样计算出的向量p，恰好是这个垂直向量所代表的方向，大小是平行四边形的面积。只有满足这样，才能保证右侧行列式的意义是这个六面体的体积。

线性方程组和矩阵的关系

Gramer法则

对于n个未知数n个方程的线性方程组，其系数行列式 $D!=0$，也就是没有降维，保持满秩，此时方程存在唯一解。解可以用【系数行列式子中第j列的元素依次用方程组右端的常数代替后的n阶行列式】/ D 来分别计算。

高斯消元法求逆矩阵

• 判断逆矩阵是否存在：以下三条是常用的等价条件和简单证明。
  

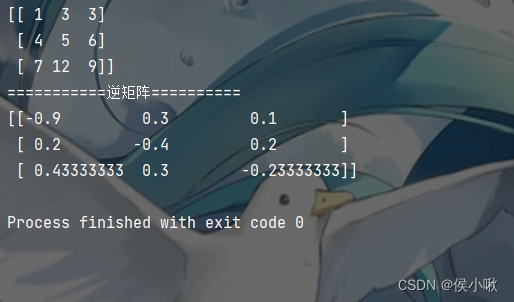
• 求逆矩阵：我们知道一个矩阵可逆后，有 $A^{-1}A=E$，下面就是怎么计算这个逆，有一种矩阵叫做初等矩阵，也就是【单位矩阵经过一次初等变化得到的矩阵】，这里的初等变化实际上对应的就是方程的加减和乘，左乘行变化，右乘列变化。所以当我们通过一系列初等变化，把A变成E的时候，E就被施加了同样的变化，也就是从A变到E的过程单独拿出来，是A$-1$。推广后的公式如下。

  $(A|B)-行变化->(E|C)$ ，有 $C=A^{-1}B$

  $(\frac{A}{B})-列变化->(\frac{E}{C})$ ，有 $C=B{A}^{-1}$

解方程组

前面提到，矩阵最初的初衷是用于解线性方程组，也是表示空间变化的一种形式。首先讨论解的形式：取决于系数矩阵和增广矩阵秩的大小。齐次方程中，【满秩时只有唯一（零）解，不满秩时有无穷多解，且解的维度为n-R(A)】。非齐次中，【系数矩阵等于增广矩阵秩的时候有解，且满秩时唯一解，不满秩时无穷多解，否则无解】。

知道了解的形式之后，可以通过【令 n-R(A) 个 “并不影响方程组” 的未知系数分别为1】来确定一组线性无关的基础解系，也就是通过代数求出某组解的方法，加以自由系数来表示通解。而非齐次方程组可以看作 $A(X+X^{\prime })=0+b$ 的形式，也就是齐次线性方程组的解 $X$ 加上一组特解 $X^{\prime }$ 。下面举例。

• 齐次线性方程组：
  

• 非齐次线性方程组：

上面使用的都是最普通的求解法，其实在取一组线性无关的基础解系那一步可以不取常数0和1，而是直接取k来代表更普通的情况，此时把k提出来，就是上面的自由系数。

补充一点，什么样的矩阵代表了这个方程组可解呢，答案是当化简到只有一个未知数在一个方程中，以此类推，第二个方程允许有包含了这个可解未知数除外的另一个未知数，也就是两个未知数前的系数可以不为0…最终我们可以得到一个上三角（或者下三角）矩阵，也就说明了为什么在解方程组时【增广矩阵的左侧化简到上三角或下三角】就可以停止啦。

参考资料

• 如何更好理解矩阵乘法
• 刘梳子数学——MIT线性代数笔记
• 3blue1brown【官方双语/合集】线性代数的本质 - 系列合集
• 线性代数与空间解析几何（第四版）