矩阵的定义

形如：

叫做m*n阶矩阵，可记为(aij)或(aij)m × n

note：
若m=n 称为n阶方阵
若 A = 0 ，则 矩阵中任意元素为零

同型矩阵

Anm Bnm 称为同型矩阵
若 任意 aij = bij 则两矩阵相等

运算

1、同型矩阵可加减

2、矩阵乘以k（≠0），矩阵中所有元素乘以k

3、Amn * Bns = Cms

  C中任意元素cij 为 A的第i行与B的第j列 乘积和

（内标相同可乘，外标相等确定型）

NOTE 1:A≠0 推不出 A^k≠0AB 不一定等于 BA矩阵相乘可以因式分解，但要注意AB 不一定等于 BAA*B= A*C  （A≠O）推不出 B = C方程组可以表示
BT= X
BT= 0

NOTE 2：
1、（A+B）*C = A*C + B*C；A*（B+C）= A*B+A*C；
2、A*（B*C） = （A*B）*C；
3、kA*（lB） = kl * A *B；
4、 E*A = A ； A*E = A；
5、O*A = O ； A*O = O；

Note3:
1、|A*B|=|A|*|B|  方阵的行列式计算

4、转置矩阵

将矩阵A的行列互换所得的矩阵，叫做转置矩阵 记 A^T

Note:
1、 (A^T)^T = A
2、 (kA)^T = kA^T
3、(A + B)^T = A^T + B^T
4、 (AB)^T = B^T A^T

5、 伴随矩阵

方阵 的各元素的代数余子式 所构成的如下矩阵A* ：

称为A的伴随矩阵

note:
1、AA* = A*A =|A|·E 
2、二阶矩阵伴随矩阵的求法：主对角线互换，副对角线变号

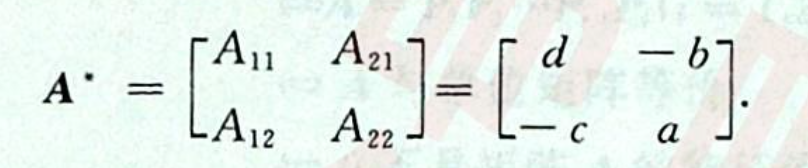
伴随矩阵的公式：

6、逆矩阵(矩阵的逆理论）

1、若A* B = E 且 B*A=E 则称 B为 A的逆矩阵，记A^-1

矩阵的逆理论：
1、可逆矩阵的逆矩阵是唯一的
2、n阶矩阵A可逆等价于：
①|A|≠0
②r（A) = n
③A的行/列向量组线性无关
④A=P1*P1....Pi, Pn(n=1,2,3...i)为初等矩阵
⑤A 等价于 单位矩阵
⑥0不是A的特征值
3、A是n阶矩阵，若AB=E，则BA= E
4、矩阵A、B等价的充分必要条件为：存在可逆矩阵P、Q，使得 PAQ = B

2、逆矩阵的公式
(A^-1)^-1 = A
(kA^-1)^-1 = 1/k * A^-1
(AB)^-1 = B^-1 A^-1
|A^-1| = 1/|A|
(A^-1)^T = (A^T)^-1
(Aⁿ)^-1 = (A^-1)ⁿ
A^-1 = A^* /|A|

7、行阶梯矩阵

满足以下两个条件：
1、若有零行，则零行一定在最底下
2、非零行主元的列下标随着行下标的增大而严格增大

最简行阶梯矩阵或行最简矩阵
如果还满足：非零行主元为 1 ，且主元所在列的其他元素都为零 0 ，称为行最简矩阵

8、正交矩阵

若 A* A^T = A^T*A = E 则称A为正交矩阵

Note:
1、A^T =A^(-1)
2、|A ^2| = 1

矩阵的初等变换

初等变换：
1、互换矩阵的某一行/列
2、用非零数 k 乘以矩阵的某一行/列
3、将 矩阵某行/列的 k 倍加到另一行/列

矩阵等价：若 B 是由A 经过 有限次的初等变换得到，则 B 与 A 等价

初等矩阵： 单位矩阵经过一次初等变换得到的矩阵

1、用初等矩阵P左乘矩阵A，相当于对A做一次初等行变换；、用初等矩阵P右乘矩阵A，相当于对A做一次初等列变换；Pij：对调两行/两列Pi(k)：将第i行列 乘以不为零的数kPij（k）：左乘-将第j行的k倍加到第行；右乘-将第i列的k倍加到第j行2、初等矩阵可逆，其逆是同类型的初等矩阵Pi(k)   逆矩阵  Pi(1/k)Pij     逆矩阵Pij pij(k） 逆矩阵Pij(-k)3、矩阵经过初等变换后，秩不变

矩阵理论

矩阵的逆理论—见逆矩阵

矩阵的秩理论

一、定义：对矩阵A， 取n行与n列，相交的部分组成A的一个n阶子式Dn*n，
①存在n阶方阵D，|D|≠ 0；
②对于任意n+1阶方阵D， |D| = 0；
则矩阵的秩为r(A)= n ；

Note
1. An*m  r(A)≤n;r（A)≤m
2.对于An*1(列向量）r(A)= 0 A = 0；r(A) = 1  A≠0；
3.①|A|≠0等价于②r（A) = n等价于A可逆称A为非奇异矩阵   或者  A满秩

2、求法：矩阵阶梯化 化为 行阶梯矩阵 最后有n个非零行 r(A) = n

Note:
r(A) = 0 , A = 0;
r(A) ≥ 1 , A ≠ 0；
r(A) ＝2 ， 至少两行不成比例

3、性质
①r(A) = r(A^T) = r(AA^T) = r(A^TA)

见到AA^T 、A^TA 使用

②r(A±B) ≤r(A) + r(B)

note：
1、见到：r(A±B)、r(A) + r(B) 使用
2、P、Q 为列向量，P^TQ 为一个数， PQ^T 为一个方阵
见到 r(PP^T + QQ^T) 使用

③r(AB) ≤ min { r(A) ,r(B) }

见到 r(A) 、 r(B) 、R(AB) 使用

④ Ans Bsm AB = 0 ， 则r(AB) ≤ n ;

⑤若P、Q 可逆 则 r(A) = r(PA) = r(AQ) = r(PAQ)

⑥ r(A^*) 的取值

case1: r(A) = n 满秩 ， r(A^*) = n ；
case2:r(A) = n-1 , r(A^*) = 1;
case3:r(A) ≤ n-2 , r(A^*) = 0;

⑦