一.线性方程组和矩阵

1.概念

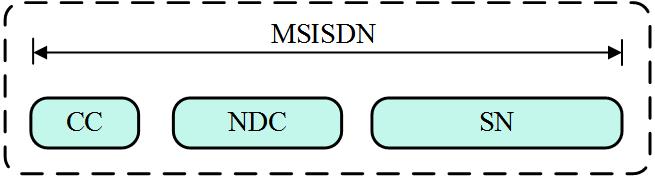
如图所示，该矩阵称为m行n列矩阵

若行数和列数都等于n，则该矩阵称为n阶方阵

两个矩阵的行数相等，列数也相等，就称它们为同型矩阵

若A=（aij）和B=（bij）是同型矩阵，且aij=bij（i=1,2,...,m;j=1,2,...,n），则称矩阵A与矩阵B相等，记作A=B

2.特殊矩阵

行矩阵：只有一行的矩阵

列矩阵：只有一列的矩阵

零矩阵：元素为0的矩阵

单位矩阵：主对角线上元素为1，其余元素为零的矩阵

对角矩阵：不在主对角线上的元素都为零 A=diag（λ1λ2,...,λn）

3.线性方程组

线性方程组分为非齐次线性方程组和齐次线性方程组

非齐次线性方程组，系数矩阵和增广矩阵

齐次线性方程组，系数矩阵

4.线性变换

如图所示，称为从变量xxx到变量yyy的线性变换，它们的关系是一一对应，系数矩阵如图

二.矩阵的运算

1.矩阵的运算

矩阵的加法：A+B=B+A，(A+B)+C=A+(B+C),A-B=A+(-B)，只有同型矩阵才能相加减

数与矩阵相乘：(λμ)A =λ(μA)，(λ+μ)A=λA+μA，λ(A+B)=λA+λB，一个数乘矩阵要将这个数与该矩阵的每一个元素相乘

矩阵的乘法：C=AB，(AB)C=A(BC)，λ(AB)=(λA)B=A(λB)，A(B+C)=AB+AC，(B+C)A=BA+CA

一般来说，AB=BA不成立，当A的列数与B的行数相等时，才能进行AB运算

A!=O，B!=O，但是AB可能为O

由Ax=0不能推断出x=0

矩阵的转置AT，(AT)T=A，(A+B)T=AT+BT，(λA)T=λAT，(AB)T=BTAT

一般AT!=A，当AT=A时，A为对称矩阵

方阵的行列式：|A|=detA

运算规律：|AT|=|A|，(λA)=λn|A|，|AB|=|A||B|

矩阵是一个数表，而行列式是一个数，方阵才能求行列式

2.特殊矩阵

伴随矩阵：行列式|A|的每一个元素的代数余子式Aij构成的矩阵

A*A=AA*=|A|E，(A*)T=(AT)*，|A*|=|A|n-1

(A*)*=|A|n-2*A，(AB)*=B*A*，(kA)*=kn-1A*

数量矩阵：单位矩阵E与数k相乘所得的矩阵

|kE|=kn
对称矩阵：满足AT=A的矩阵

aij=aji，i,j=1,2,...,n

反称矩阵：满足AT=-A的矩阵

aij=-aji，且aii=0，i,j=1,2,...,n

3.习题

题型一：与矩阵加法相关的问题

证明任何一个n阶方阵都可以表示为一对称矩阵与一反对称矩阵之和

证明：

设A可分解为一对称矩阵B与一反对称矩阵C之和，则A=B+C，且BT=B，CT=-C

所以AT=(B+C)T=BT+CT=B-C

解得B=1/2(A+AT)，C=1/2(A-AT)

A=B+C有解，所以原命题成立

题型二：与矩阵乘法相关的问题

|A+AB|=0可以推出|A|=0或者|E+B|=0

注意提出公因式A后，不是1+B，而是E+B

题型三：与矩阵乘法交换性相关的问题

设A，B为n阶方阵，且满足A2=A，B2=B，(A+B)2=(A+B)，证明AB=BA=O

思路：在证明AB=BA时，可以先证明AB，BA都等于同一个矩阵，注意在(A+B)2!=A2+2AB+B2

证明：

由于A2=A，B2=B，则有(A+B)2=A2+AB+BA+B2

而(A+B)2=(A+B)，所以AB+BA=O

用A左乘上式可得A2B+ABA=AB+ABA=O，用A右乘上式可得ABA+BA2=ABA+BA=O，

从而得到AB=-ABA=BA，故有AB=BA=O

题型四：与伴随矩阵相关的问题

涉及伴随矩阵的计算或者证明的问题，常用公式

A*A=AA*=|A|E，(A*)T=(AT)*，|A*|=|A|n-1

(A*)*=|A|n-2*A，(AB)*=B*A*，(kA)*=kn-1A*

题型五：与特殊矩阵相关的问题

涉及证明是否为对称矩阵或非对称矩阵的题，先把原式进行转置，看转置后的式子是否符合对称矩阵或者非对称矩阵的定义

例如：
设A为n阶方阵，证明A-AT不是对称矩阵，对A-AT进行转置，即(A-AT)T=AT-A!=A-AT

故该矩阵不是对称矩阵

题型六：求An的问题

已知α=(1,2,3)，β=(1,1/2,1/3)，设A=αTβ，其中αT是α的转置，求An

解：

αTβ为一个3*3矩阵，而βαT=3为一个数字

An=(αTβ)(αTβ)...(αTβ)=αT(βαT)(βαT)...(βαT)β=αT(βαT)n-1β=3n-1*AαTβ

解题思路：
求矩阵的高次幂时，经常要用到矩阵乘法的结合律

结论：

1.设α=(a1,a2,...,an)，β=(b1,b2,...,bn)，且A=αTβ，则An=kn-1A，其中k=a1*b1+a2*b2+...+an*bn

2.A=B+C且BC=CB，则An=(B+C)n

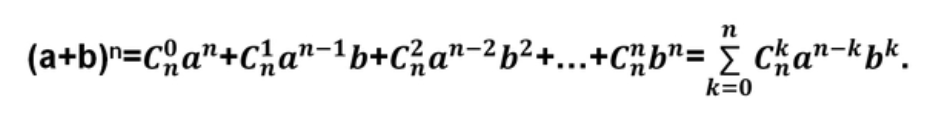
题型七：求方阵的行列式

题型八：代数余子式与A*相关的问题

题型九：关于乘法交换性常用结论的证明

解题时，先设出于任意n阶方阵可交换的方阵，并用Eij这些特殊矩阵与其相乘，设法求出此矩阵应满足的条件

三.逆矩阵

1.逆矩阵

定义

对n阶矩阵A，若有n阶矩阵B使AB=BA=E，则称A可逆，且A-1=B

求法

若AB=E(或BA=E)，则B=A-1

若|A|!=0，则A可逆，且A-1=A*/|A|

初等变换法：初等行变换

可逆判定

A是可逆矩阵，则|A|!=0

性质

若A可逆，则A-1，A*也可逆，且(A-1)-1=A，(A*)-1=(A-1)*=A/|A|

若A可逆，数λ!=0，则λA也可逆，且(λA)-1=A-1/λ

若A，B为同阶矩阵且可逆，则AB也可逆，且(AB)-1=B-1A-1

若A可逆，则AT也可逆，且(AT)-1=(A-1)T

2.矩阵的多项式

3.习题

题型一：求一般矩阵的逆矩阵

方法一：利用伴随矩阵求A的逆矩阵

方法二：直接利用定义求解

对于高阶矩阵，方法二烦琐且易出错，通常使用方法一

注意在使用方法一时，要先证明该矩阵可逆，即证明该矩阵行列式不等于0

若遇到求(A*)-1，利用公式AA*=|A|E来直接计算(A*)-1，简化了计算过程，此外，若|A|!=0(证明|A|可逆)，

则(A*)-1=(|A|A-1)-1=A/|A|

题型二：求抽象矩阵的逆矩阵

设A为n阶方阵且满足条件A2+A-6E=O.求

1.A-1，(A+E)-1

2.(A+4E)-1

解：

1.由于A2+A-6E=O，所以有A(A+E)=6E，从而A*(A+E)/6=E，所以A可逆，并且A-1=(A+E)/6，同理可得，(A+E)可逆，并且(A+E)-1=A/6

2.由A2+A-6E=O可得(A+4E)(A-3E)+6E=O，可得(A+4E)(A-3E)=-6E，即(A+4E)(A-3E)/-6=E，因而A+4E可逆，并且(A+4E)-1=-(A-3E)/6

解题思路：

解题时，通过矩阵的运算找到一个形如AB=E的等式，利用矩阵的定义得出A-1=B或B-1=A，该解法的关键是等式AB=E的寻找，并结合已知和所求的特点仔细观察

若方阵A可分解成多个可逆矩阵乘积的形式，则A可逆，可通过两边取行列式或直接求用乘积形式表示的逆矩阵来证明

题型三：矩阵可逆性判定

设A，B均为n阶方阵，则必有A或B不可逆，必有AB不可逆

|AB|=|A||B|!=0，必有|A|!=0，|B|!=0

即，若AB可逆，必须要求A，B同时可逆，若AB中有一个不可逆，则AB必定不可逆

设n阶矩阵A和B满足条件A+B=AB，证明A-E为可逆矩阵，其中E是n阶单位矩阵

由A+B=AB可得AB-A-B=O，所以AB-A-B+E=E

从而可得(A-E)(B-E)=E，所以(A-E)可逆

题型四：解矩阵方程

解题思路：先求出A-1，然后代入题目要求的式子中求解

在用到某一个矩阵的逆矩阵时，要先说明其逆矩阵存在的合理性

题型五：矩阵多项式的运用

解题时，先将矩阵方程进行整理，然后把矩阵B用矩阵A和单位矩阵E表示出来，再求B的行列式，注意矩阵与其逆矩阵这两者的行列式的关系

若A是对角矩阵，直接对其矩阵取逆，讲矩阵B用A-1和E表示出来

在化简矩阵方程时，主要利用关系式(AB)T=BTAT

注意使用|A*|=|A|n-1，若一致伴随矩阵，可用伴随矩阵行列式求出原矩阵行列式的值

该结论的证明过程为：

因为|A*||A|=|A*A|=||A|E|=|An|E=|A|n，所以|A*|=|A|n-1

题型六：利用逆矩阵求伴随矩阵

设A是n阶可逆矩阵，证明(A*)*=|A|n-2A，并求|(A*)*|

证明：

有公式AA*=|A|E可得A*(A*)*=|A*|E，所以(A*)*=|A*|(A*)-1

又因为|A*|=|A|n-1和(A*)-1=(A-1)*=A/|A|，所以(A*)*=|A|n-2A

所以|(A*)*|=||A|n-2A|=|A|(n-2)n|A|=|A|(n-2)n+1

求逆矩阵与伴随矩阵的行列式时，通常要用到以下几个公式

1.|AB|=|A||B|

2.AA*=|A|E

3.|A*|=|A|n-1

4.|A-1|=|A|-1

5.|λA|=λn|A|

题型七：利用矩阵求数的关系

四.克拉默法则

1.克拉默法则

2.克拉默法则的应用

线性方程组，若系数行列式D!=0，则有唯一解，若无解或有两个不同的解，则D=0

齐次线性方程组，若系数行列式D!=0，则只有零解，若有非零解，则D=0

3.习题

题型一：应用克拉默法则求方程组的解

题型二：已知线性方程组及其解的情况，求方程组的系数

题型三：讨论行列式与方程组解的关系

五.矩阵分块法

1.分块矩阵

将矩阵A用若干条纵线和横线分成许多个小矩阵，每个小矩阵称为A的子块，以子块为元素的形式上的矩阵称为分块矩阵

2.常用分块方法

按行分块

按列分块

对角块矩阵

2*2矩阵

如图所示：

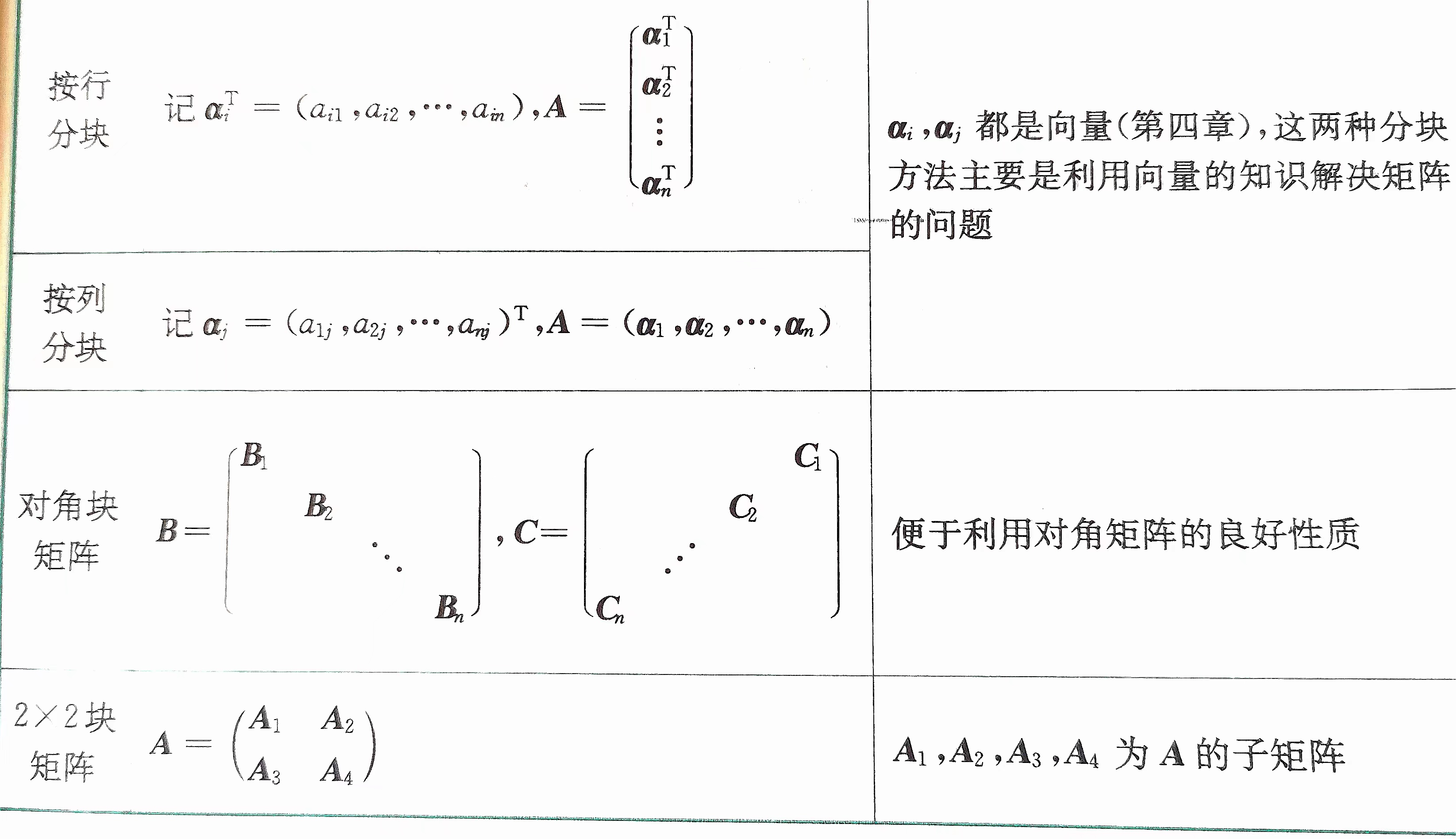
3.分块矩阵的运算规则

分块矩阵的加法

分块矩阵的数乘

分块矩阵的乘法

分块矩阵的转置

分块对角矩阵

分块矩阵的逆矩阵

4.习题

题型一：分块矩阵的运算

加法：将A,B分块后，对应子块分别相加，在对A，B分块时应注意分块后对应的子块应是行数和列数相同的矩阵

乘法：将矩阵A和矩阵B进行适当分块，再利用分块矩阵的乘法进行运算，在进行运算时，要保证A的列与B的行的分法相同

题型二：利用分块矩阵求逆矩阵

对矩阵进行分块时一定要注意观察，分开后各块的逆矩阵应更易求，最好是有对角矩阵存在

题型三：分块矩阵常用结论的证明

本章知识总结

定义：当m=n时，Am*n也称为n阶矩阵

运算：

矩阵的加法：A+B

数与矩阵相乘：λA

矩阵的乘法：AB

矩阵的转置：AT

方阵的行列式：|A|

逆矩阵A-1：

求逆矩阵

A可逆==|A|

证明矩阵可逆

特殊矩阵：

零矩阵O

对角矩阵A

单位矩阵E

对称矩阵AT=A

反对称矩阵AT=-A

克拉默法则

分块矩阵

1.关于矩阵运算的小结

矩阵相加时，两矩阵必须是同型矩阵才能相加，而矩阵的乘法运算更特殊，要求第一个矩阵的列数等于第二个矩阵的行数，并且矩阵的乘法通常不满足交换律，而且若A!=O，A!=O，则有AB=O

2.关于分块矩阵的小结

高阶矩阵运算时分块更有利于计算，分成一些低阶子矩阵后再作运算会大大简化计算，矩阵在分块时尽量使子块称为对角矩阵、零矩阵或者特殊矩阵，并且两高阶矩阵运算时，要使两矩阵分块后的子块符合矩阵的运算规则

3.关于求逆矩阵的小结

求逆矩阵的方法主要有伴随矩阵法、定义法、分块矩阵法，伴随矩阵求逆矩阵主要利用公式A-1=A*/|A|，定义法是先设出矩阵A的逆矩阵B，利用等式AB=BA=E，求出B，分块矩阵法主要用于求高阶矩阵的逆矩阵

4.关于求矩阵方程的小结

常见的矩阵方程有一下形式：

AX=C

XB=C

AXB=C

若AB可逆，方程的解围X=A-1C，X=CB-1，X=A-1CB-1

5.关于克拉默法则的小结

克拉默法则是线性方程组求解的基础，它提供了线性方程组是否有解的判定标准，并给出了求解的方法，用克拉默法则求解方程组是进行行列式的计算