目录
1. 矩阵是什么?
2. 几种特殊的矩阵
3. 矩阵的运算
4. 方阵的行列式
5. 伴随矩阵
6. 矩阵初等变换
7. 矩阵的秩
8. 初等矩阵
1. 矩阵是什么?
矩阵被认为是线性代数中最基础的内容, 也是研究线性代数其他内容的工具。
由m*n个数按一定的次序排成的m行n列的矩形数表称为m*n 的矩阵,简称矩阵:

横的各排称为矩阵的行,竖的各排称为矩阵的列.称为矩阵的第i行j列的元素.元素为实数的矩阵我们称为实矩阵,我们目前只讨论实矩阵。
矩阵通常用大写字母A、B、C等表示,如:

简记为.
行矩阵:
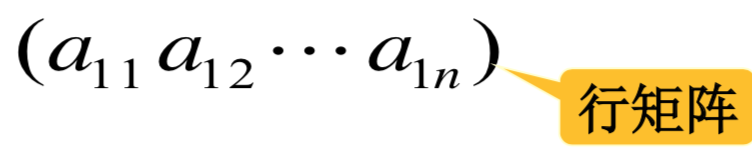
列矩阵:
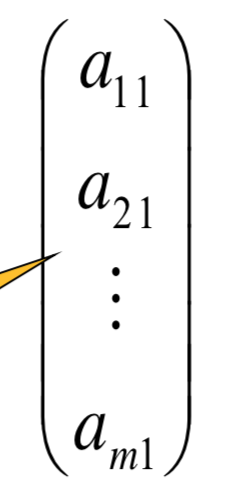
矩阵是翻译过来的词,英文是Matrix,这个翻译很 好。既形象又大气。阵这个词很容易让我们想到那种气势庞大的阵列。 让你感觉到那种重要和不可替代。
2. 几种特殊的矩阵
- 方阵
当m=n时,即矩阵的行数与列数相同时, 称矩阵为方阵。

主对角线从左上到右下,元素的下标相同,即i=j. 注意只有方阵才有主对角线。
斜对角线从右上到左下,只有方阵才有斜对角线。
- 零矩阵

- 对角矩阵
对角矩阵首先得有对角线,所以必须是方阵。

其它没写出的元素都是零。
- 单位阵
若对角线上的元素都是1,就得到又一个特殊的矩阵:

这个矩阵称作单位矩阵,记作或
。
- 数量矩阵
若对角线上的元素是相同的数k,得到的特殊矩阵为:

这个矩阵称作数量矩阵。
- 三角阵
上三角矩阵:

下三角矩阵:

- 梯形阵
设为非零矩阵,若非零行(即至少有一个非零元素的行)全在零行的上面, A中各非零行中第一个(最后一个)非零元素前(后)面零元素的个数随行数增大而增多(减少),则称为上(下)梯形矩阵。简称为上(下)梯形阵。

3. 矩阵的运算
线性运算:
- 相等
两个矩阵相等是指这两个矩阵有相同 的行数与列数, 且对应元素相等.即:

- 加、减法
矩阵加减必须是同型的,对应位置元素相加减:
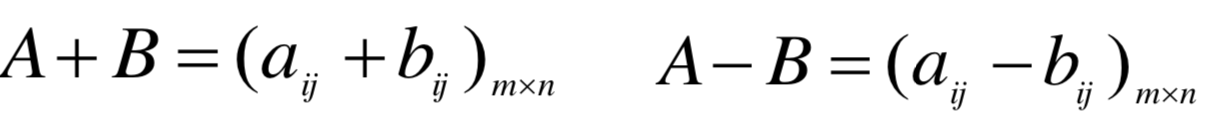
运算规律:
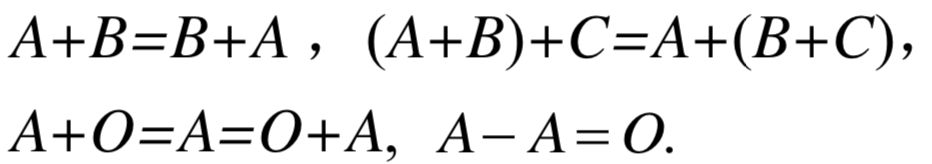
负矩阵:
的负矩阵为
,记作-A,即
- 数乘

与数的乘法,简称为数乘。记作:

数k乘矩阵中的每一个元素。
运算规律:
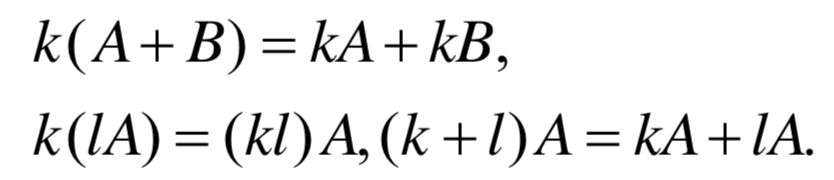
- 矩阵乘法
(A的列数必须等于B的行数):

注意:
1),矩阵乘法不满足交换率.
2),不满足消去率;
3)有非零的零因子。
运算规律:

- 练习

(对角阵相乘等价于直接对应位置元素相乘)。
其他运算:
- 方阵的正整数幂

注意成立的条件是
.
- 矩阵的转置
行列互换。

运算规律:

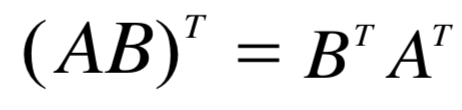
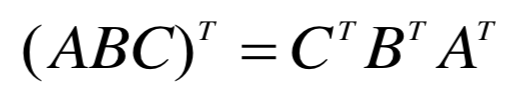
- 对称阵与反对称阵(方阵)
对称阵:
下面的几个矩阵都是对称阵:

反对称阵:
且
下面这个矩阵是反对称阵:
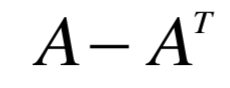
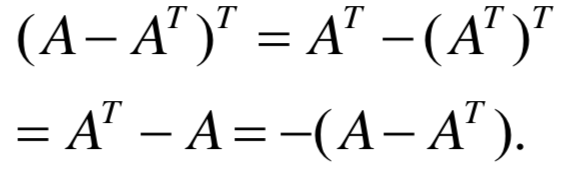
任一方阵都可以分解成 对称阵与反对称阵的和:
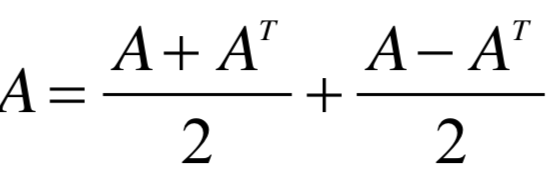
- 练习
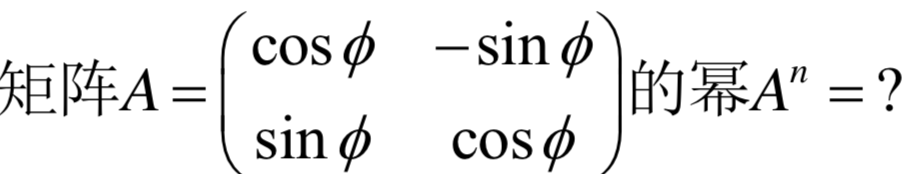

数学归纳法:

4. 方阵的行列式
由方阵A所构成的行列式称为方阵的行列式,记为或
若方阵的行列式不为零,则称方阵为 非奇异方阵,否则称为奇异方阵.

由方阵A所确定的行列式作为一种运算除具有一般的行列式的性质外,还有如下性质:
设A, B均为n阶方阵,k为常数,则有:

- 练习
奇数阶反对称阵的行列式为零:

5. 伴随矩阵


写伴随矩阵时,注意代数余子式的顺序。

主对角线元素互换,斜对角线元素取相反数。


6. 矩阵初等变换
以下三种变换分别称为矩阵的第一、第二、第三种初等变换:

矩阵的初等行变换与初等列变换统称为初等变换。
初等变换可以简化矩阵,如将矩阵化为梯形阵。

- 矩阵等价
对矩阵A实行有限次初等变换得到矩阵B,则称矩 阵A与B等价,记作.
等价矩阵具有自反性、对称性、传递性。即
![]()


7. 矩阵的秩
- k阶子式
在中任取k行k列,位于这些行列相交处的
个元素,按原次序组成的 k阶行列式,称为矩阵A的k阶子式.一般地,m*n矩阵A的k阶子式有
个。

- 矩阵的秩
矩阵 A 的所有不等于零的子式的最高阶 数称为矩阵 A 的秩。记作.
显然:r(O)=0;只要A不是零矩阵, 就有 r(A)>0.并且:

任意一个矩阵都可经初等变换化为梯形阵.梯形阵的秩等于其非零行的行数.矩阵经初等变换后其秩不变.
原矩阵的秩就等于经初等变换后得到的梯形矩阵的秩,即梯形矩阵非零行的行数。
用初等变换求矩阵的秩:

- 练习
将秩与行列式结合:



矩阵的秩是矩阵的一个重要的数字特征。
显然,若两个矩阵有相同的秩,则这两个矩阵有相同的标准形,从而等价;反之,若两个矩阵等价,则它们的秩相同。
矩阵A与B等价的充要条件是r(A)=r(B).
- 满秩矩阵
若方阵A的秩与其阶数相等,则称A为满秩矩阵; 否则称为降秩矩阵。
设方阵A为满秩阵,则A的标准形为同阶单位阵 E .即:
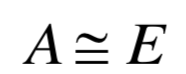
若方阵A的行列式 ,则称A为非奇异矩阵,A是满秩的,即
; 若
,则称为A为奇异矩阵,A是降秩的,即
。
8. 初等矩阵
对单位阵进行一次初等变换后得到的矩阵称为初等矩阵。
三种初等行变换得到的初等矩阵分别为:
1)互换第i、j行:

2)第i行乘以k:

3)第j行乘以k加到第i行:

对单位阵作一次列变换得到的矩阵也包括在上面的三类矩阵之中。
- 初等矩阵的性质
1)初等矩阵的转置仍为同类型的初等矩阵.


2)初等矩阵都是非奇异的.
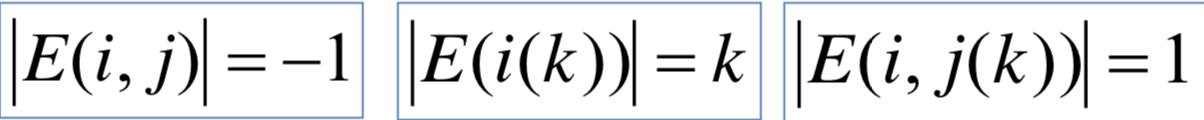
- 初等矩阵和初等变换的关系


初等行变换相当于左乘初等矩阵; 初等列变换相当于右乘初等矩阵.


- 满秩矩阵
若方阵A的秩与其阶数相等,则称A为满秩矩阵; 否则称为降秩矩阵。
设A为满秩阵,则A的标准形为同阶单位阵 E .即
![]()
以下命题等价:


矩阵A与B等价的充要条件为存在m阶及n阶满秩阵P、Q,使得,
由此还可得到:若P、Q为满秩阵,则:
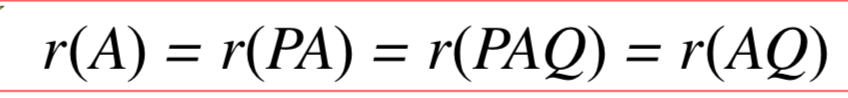
- 练习