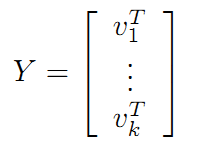矩阵的 SVD 分解方法，几何意义

转自：
https://liam.page/2017/11/22/SVD-for-Human-Beings/
更多信息请读者移步原文阅读。
推荐中国台湾周志成老师的线性代数博客
https://ccjou.wordpress.com/
以及书籍《矩阵分析及应用》-- 张贤达
还可参考：
https://www.cnblogs.com/endlesscoding/p/10058532.html

一、一些矩阵基本知识

1.1.矩阵的转置及共轭转置

矩阵的转置（transpose）是最简单的一种矩阵变换。简单来说，若 m×n 的矩阵 M 的转置记为 M^?；则 M^? 是一个 n×m 的矩阵，并且 M_i,j=M^?_j,i。

因此，矩阵的转置相当于将矩阵按照主对角线翻转；同时，我们不难得出 M=(M^?)^?。

关于矩阵的一些性质：
(A + B)^T = A^T + B^T;
(AB)^T = B^TA^T;
(AB)^-1 = B^-1A^-1;
(A^-1)^T = A^T)^-1 （此时A必须是可逆方阵）;

矩阵的共轭转置（conjugate transpose）可能是倒数第二简单的矩阵变换。共轭转置只需要在转置的基础上，再叠加复数的共轭(M^*)即可。因此，若以 M^? 记矩阵 M 的共轭转置，则有
M^H = (M^*)^T = (M^T)^*

1.2.正交矩阵及酉矩阵

满足U^T U = UU^T = E(E为单位矩阵）的实方阵，成为正交矩阵。

酉矩阵（unitary matrix）是一种特殊的复方阵，它满足

UU^?=U^?U=I_n.

不难看出，酉矩阵实际上是推广的正交矩阵（orthogonal matrix）；当酉矩阵中的元素均为实数时，酉矩阵实际就是正交矩阵。另一方面，由于 MM⁻¹=M⁻¹M=I_n，所以酉矩阵 U 满足 U⁻¹=U^?；事实上，这是一个矩阵是酉矩阵的充分必要条件。

1.3.正规矩阵

复方阵M满足MM^?=M^?M，则称M为正规矩阵。
复系数的酉矩阵和实系数的正交矩阵都是正规矩阵。但正规矩阵并不只有酉矩阵或正交矩阵。
例如说，矩阵 $\mathbf{M}=\left(\begin{array}{lll}{1} & {1} & {0} \\ {0} & {1} & {1} \\ {1} & {0} & {1}\end{array}\right)$ 即是一个正规矩阵，但它显然不是酉矩阵或正交矩阵；因为
$\mathbf{M} \mathbf{M}^{\mathrm{H}}=\left(\begin{array}{lll}{2} & {1} & {1} \\ {1} & {2} & {1} \\ {1} & {1} & {2}\end{array}\right)=\mathbf{M}^{\mathrm{H}} \mathbf{M}$

酉矩阵相关性质：
在这里插入图片描述

1.4 Hermitian矩阵

满足A = A^H 的复方阵称为Hermitian矩阵。

二、谱定理和谱分解

矩阵的对角化是线性代数中的一个重要命题。谱定理（spectral theorem）给出了方阵对角化的一个结论：若矩阵 M 是一个正规矩阵，则存在酉矩阵 U，以及对角矩阵 Λ，使得 M=UΛU^?.

这也就是说，正规矩阵，可经由酉变换，分解为对角矩阵；这种矩阵分解的方式，称为谱分解（spectral decomposition）。

三、奇异值分解（SVD）

谱定理给出了正规矩阵分解的可能性以及分解形式。然而，对于矩阵来说，正规矩阵是要求非常高的。因此，谱定理是一个非常弱的定理，它的适用范围有限。在实际生产中，我们遇到的很多矩阵都不是正规矩阵。对于这些矩阵，谱定理就失效了。作为谱定理的泛化，SVD 分解对于原矩阵的要求就要弱得多。

3.1SVD的定义

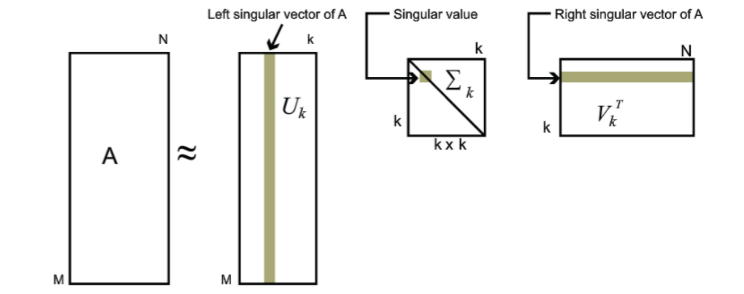
SVD 的定义：假设 M 是一个 m×n 的矩阵，其中的元素全部属于数域 ?（实数域 ℝ 或复数域 ℂ）。那么，存在 m×m 的酉矩阵 U 和 n×n 的酉矩阵 V 使得M=UΣV^?,

其中 Σ 是 m×n 的非负实数对角矩阵；并且 Σ 对角线上的元素 Σ_i,i是 M 的奇异值。一般来说，我们偏好将这些奇异值按从大到小的顺序排列，这样一来 Σ 就由 M 唯一确定了。

另一方面，因为 U 和 V 都是酉矩阵，所以 U 和 V 的列向量分别张成 ?m 和 ?n 的一组标准正交基。我们将 U 的列向量记作 $\vec{u}_{i}$ , 1⩽i⩽m；将 V 的列向量记作 $\vec{v}_{j}$ ,1⩽j⩽n；同时，将 Σ 对角线上的第 i 个元素记作 σ^k,1⩽k⩽min(m,n)。那么，SVD 分解实际可以将矩阵 M 写作一个求和形式
$\mathbf{M}=\sum_{i=1}^{\min (m, n)} \sigma_{i} \vec{u}_{i} \vec{v}_{i}^{\top}$

3.2 SVD 的计算方法

了解了 SVD 的介绍和相关几何解释之后，接下来最直接想要知道的就是如何计算一个矩阵的 SVD 了。我们分成几步来探讨这个问题。

3.2.1SVD 与特征值

我们对求特征值和特征向量比较熟悉，一般分两步：

求出所有使矩阵A - λI奇异的λ（特征值）即求出det(A - λI) = 0的所有根；
将λ带入A - λI，求出所有使(A - λI) $\vec{x}$ = $\vec{0}$ 成立的 $\vec{x}$ ，它们是于λ对应的特征向量；

推论1：若A ∊ ℂ^nxn为Hermitain矩阵，其特征值一定是实数，并且有A= UΣU^H,式中U = [u₁,u₂,…,u_n]^T; Σ = diag(λ₁,λ₂,…,λ_n)。
证明：因为对于任意 Hermitain矩阵A的特征值λ_i都有对于的特征向量 $\vec{u}_{i}$ ((!= $\vec{0}$ )满足下列关系：
$\boldsymbol{A} \boldsymbol{u}_{i}=\lambda_{i} \boldsymbol{u}_{i}, \quad i=1,2, \cdots, n$
将这些方程写成矩阵的形式：
$\boldsymbol{A}\left[\boldsymbol{u}_{1}, \cdots, \boldsymbol{u}_{n}\right]=\left[\boldsymbol{u}_{1}, \cdots, \boldsymbol{u}_{n}\right]\left[\begin{array}{ccc}{\boldsymbol{\lambda}_{1}} & {} & {0} \\ {} & {\ddots} & {} \\ {0} & {} & {\lambda_{n}}\end{array}\right]$
令U = [u₁,u₂,…,u_n]^T; Σ = diag(λ₁,λ₂,…,λ_n)，所以有
$\boldsymbol{A} \boldsymbol{U}=\boldsymbol{U}\Sigma$
（?证不下去了，显然下一步要在等式两边同右乘U^H,然后证明U是酉矩阵，即UU^H = E。线性代数中在讲对称矩阵的性质的时候给出定理：对于n阶实对称矩阵A，存在正交矩阵Q，使得A = QΣQ^T，现在只是把这个推广到复数域上了，可以参考这两个：https://www.zhihu.com/question/38801697
https://blog.csdn.net/BingeCuiLab/article/details/47209037)
现在，假设矩阵 M_m×n 的 SVD 分解是M=UΣV^?，那么我们有
$\boldsymbol{M} \boldsymbol{M}^{H}=\boldsymbol{U}\Sigma \boldsymbol{V}^{H}\boldsymbol{V}\Sigma ^{H}\boldsymbol{U}^{H}=\boldsymbol{U}\Sigma\Sigma ^{H}\boldsymbol{U}^{H}$
$\boldsymbol{M}^{H} \boldsymbol{M}=\boldsymbol{V}\Sigma ^{H}\boldsymbol{U}^{H}\boldsymbol{U}\Sigma \boldsymbol{V}^{H}=\boldsymbol{V}\Sigma\Sigma ^{H}\boldsymbol{V}^{H}$
显然MM^H 和 M^HM都是Hermitian矩阵，用推论1有：
U 的列向量（左奇异向量），是 MM^? 的特征向量；同时，V 的列向量（右奇异向量），是 M^?M 的特征向量；另一方面，M 的奇异值（Σ 的非零对角元素）则是 MM^? 或者 M^?M 的非零特征值的平方根。通过这样将问题转换，我们就可以用求特征值的方法求奇异值了。

3.2.2 SVD的计算

计算出任意矩阵的 SVD 分解的算法步骤：

计算 MM^? 和 M^?M；
分别计算 MM^? 和 M^?M 的特征向量及其特征值；
MM^? 的特征向量组成 U；而 M^?M 的特征向量组成 V；
对 MM^? 和 M^?M 的非零特征值求平方根，对应上述特征向量的位置，填入 Σ 的对角元。

Example:对矩阵M = $\left[\begin{array}{ll}{2} & {4} \\ {1} & {3} \\ {0} & {0} \\ {0} & {0}\end{array}\right]$ 进行奇异值分解。

首先，我们需要计算 MM?，
$\mathbf{W}=\mathbf{M} \mathbf{M}^{H}=\left[\begin{array}{ll}{2} & {4} \\ {1} & {3} \\ {0} & {0} \\ {0} & {0}\end{array}\right]\left[\begin{array}{llll}{2} & {1} & {0} & {0} \\ {4} & {3} & {0} & {0}\end{array}\right]=\left[\begin{array}{cccc}{20} & {14} & {0} & {0} \\ {14} & {10} & {0} & {0} \\ {0} & {0} & {0} & {0} \\ {0} & {0} & {0} & {0}\end{array}\right]$
然后，我们求 W 的特征值与特征向量。
$\left[\begin{array}{cccc}{20-\lambda} & {14} & {0} & {0} \\ {14} & {10-\lambda} & {0} & {0} \\ {0} & {0} & {-\lambda} & {0} \\ {0} & {0} & {0} & {-\lambda}\end{array}\right] \vec{x}=\overrightarrow{0}$
根据线性方程组的理论，若要该关于 $\vec{x}$ 的方程有非零解，则要求系数矩阵的行列式为 0；也就是
$\left|\begin{array}{cccc}{20-\lambda} & {14} & {0} & {0} \\ {14} & {10-\lambda} & {0} & {0} \\ {0} & {0} & {-\lambda} & {0} \\ {0} & {0} & {0} & {-\lambda}\end{array}\right|=\left|\begin{array}{cc}{20-\lambda} & {14} \\ {14} & {10-\lambda}\end{array}\right|\left|\begin{array}{cc}{-\lambda} & {0} \\ {0} & {-\lambda}\end{array}\right|=0$
这也就是 ((20−λ)(10−λ)−196)λ2=0；解得 λ1=λ2=0, λ3=15+√221≈29.866, λ4=15−√221≈0.134。将特征值代入原方程，可解得对应的特征向量；这些特征向量即作为列向量，形成矩阵
$\mathbf{U}=\left[\begin{array}{cccc}{-0.82} & {-0.58} & {0} & {0} \\ {-0.58} & {0.82} & {0} & {0} \\ {0} & {0} & {1} & {0} \\ {0} & {0} & {0} & {1}\end{array}\right]$
同理可解得（注意，MM^? 和 M^?M 的特征值相同）
$\mathbf{V}=\left[\begin{array}{cc}{-0.40} & {-0.91} \\ {-0.91} & {0.40}\end{array}\right]$
以及 Σ 上的对角线元素由 W 的特征值的算术平方根组成；因此有
$\boldsymbol{\Sigma}=\left[\begin{array}{cc}{5.46} & {0} \\ {0} & {0.37} \\ {0} & {0} \\ {0} & {0}\end{array}\right]$
因此我们得到矩阵 M 的 SVD 分解（数值上做了近似）：
$\left[\begin{array}{ll}{2} & {4} \\ {1} & {3} \\ {0} & {0} \\ {0} & {0}\end{array}\right] \approx\left[\begin{array}{cccc}{-0.82} & {-0.58} & {0} & {0} \\ {-0.58} & {0.82} & {0} & {0} \\ {0} & {0} & {1} & {0} \\ {0} & {0} & {0} & {1}\end{array}\right]\left[\begin{array}{cc}{5.46} & {0} \\ {0} & {0.37} \\ {0} & {0} \\ {0} & {0}\end{array}\right]\left[\begin{array}{cc}{-0.40} & {-0.91} \\ {-0.91} & {0.40}\end{array}\right]$