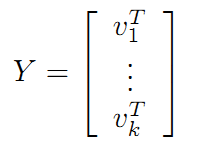点击上方“小白学视觉”，选择加"星标"或“置顶”
重磅干货，第一时间送达SVD(Singular Value Decomposition)奇异值分解分解是机器学习中最重要的矩阵分解方法。
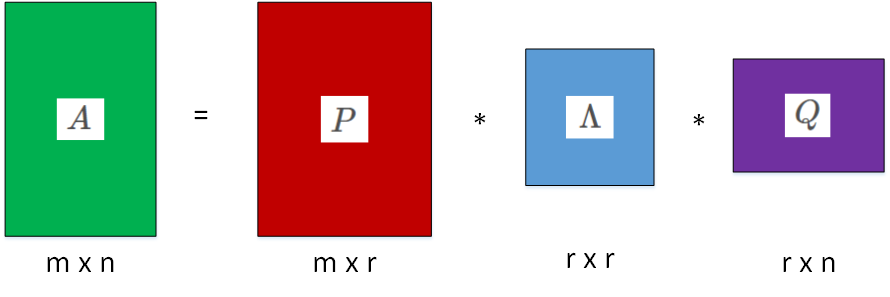
它能够将一个任意形状的矩阵分解成一个正交矩阵和一个对角矩阵以及另一个正交矩阵的乘积。
SVD分解具有非常深刻的几何含义。矩阵实际上对应着一种线性变换，一个矩阵作用到一个向量上，会得到一个新的向量。任何一个矩阵的操作效果可以分解成一次旋转，一次拉伸和维度改变，以及另外一次旋转三者作用效果的合成。
SVD分解通常用于数据压缩和数据降维。用于数据降维时，既可以对列降维，也可以对行降维，其中对列的降维等价于PCA的降维。
不仅如此，SVD算法还可以用于在声音和图像处理中剥离背景信号，在推荐算法中也经常出现它的身影。
一，SVD矩阵分解简介
SVD分解将任意矩阵分解成一个正交矩阵和一个对角矩阵以及另一个正交矩阵的乘积。
对角矩阵的对角元称为矩阵的奇异值，可以证明，奇异值总是大于等于0的。
当对角矩阵的奇异值按从大到小排列时，SVD分解是唯一的。
SVD分解有着非常深刻的几何含义。
矩阵实际上是对应着一种线性变换。一个矩阵作用到一个向量上，会得到一个新的向量。任何一个矩阵的操作效果可以分解成一次旋转，一次拉伸和维度改变，以及另外一次旋转三者作用效果的合成。
注意正交矩阵和作用到向量后是不会改变向量长度的，所以对应着旋转变换。
二，SVD分解的数学推演
可以推出
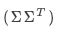依然是对角矩阵，又U为正交矩阵。
所以 
为AA^T的相似对角矩阵，其对角元为AA^T的特征值，U由其对应特征向量构成，这些向量称为A的左奇异向量。
因此
的对角元为AA^T特征值的平方根，称之为矩阵A的奇异值。
类似地V由A^TA的特征向量构成，这些向量称为A的右奇异向量。
三，SVD分解和数据压缩
奇异值描述了矩阵对应的拉伸变换在各个方向的比例，是矩阵的重要特征。
奇异值的分布通常非常不均，在很多的情况下前10%甚至1%的奇异值之和就占了全部奇异值之和的99%以上。
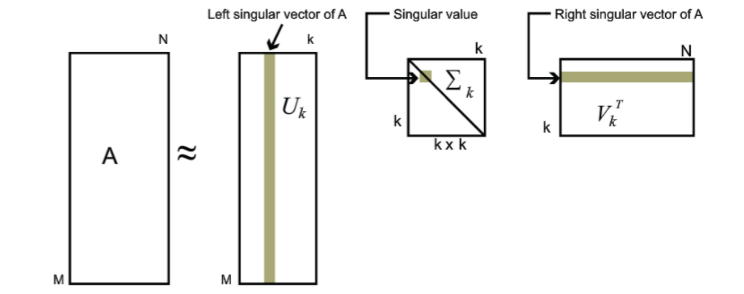
因此我们可以用前个大的奇异值来近似的描述矩阵。
这就是SVD分解用来进行数据压缩的原理。
# 下面的范例示范SVD分解用于图片数据压缩。
%matplotlib inline
%config InlineBackend.figure_format = 'svg'
import numpy as np
from matplotlib import pyplot as plt
from skimage import datadef compressBySVD(img,r):u,s,vt = np.linalg.svd(img)ur = u[:,0:r]sr = s[0:r]vtr = vt[0:r,:]return (ur,sr,vtr)def rebuildFromSVD(ur,sr,vtr):img = ur@np.diag(sr)@vtrreturn(img)img = data.camera()/255.0plt.figure(figsize=(10,8))
for i,r in enumerate([5,10,20,30,40,50,100,200],start = 1):ur,sr,vtr = compressBySVD(img,r)compress_ratio = (np.product(ur.shape) + len(sr) + np.product(vtr.shape))/np.product(img.shape)img_rebuild = rebuildFromSVD(ur,sr,vtr)ax=plt.subplot(3,3,i)ax.imshow(img_rebuild,cmap = "gray")ax.set_title("r=%d"%r+", compress_ratio=%.2f"%compress_ratio)ax.set_xticks([])ax.set_yticks([]) ax = plt.subplot(3,3,9)
ax.imshow(img,cmap = "gray")
ax.set_title("r = 512, original image")
ax.set_xticks([])
ax.set_yticks([]) plt.show()
四，SVD分解和PCA降维
PCA降维可以看成是SVD分解的一个应用。PCA降维使用的变换矩阵恰好是SVD分解的右奇异矩阵。
实际上，由于SVD分解存在着无需通过计算特征值和特征向量的可并行的数值迭代计算算法，sklearn的PCA降维算法正是通过SVD分解计算的。
假定PCA对应的正交变换矩阵为，根据PCA算法的数学原理，
由协方差矩阵
的各个特征向量组成，它能够将协方差矩阵相似对角化。
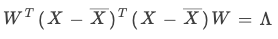
其中为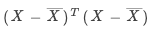
的相似对角矩阵，且对角元由大到小排列。
利用的SVD矩阵分解:
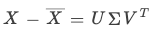
我们有
根据SVD分解的数学原理，也是 
的相似对角矩阵，且对角元由大到小排列。
于是有：
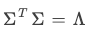
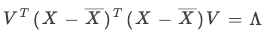
于是右奇异向量构成的矩阵 ???? 恰好是PCA算法所需要的正交变换矩阵 ????。
注意到PCA算法实际上是一种列降维的方法，实际上利用SVD分解的左奇异矩阵也可以对矩阵进行行降维。
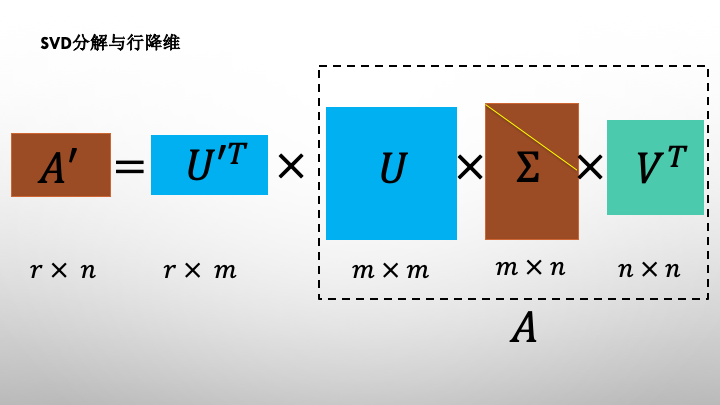
# 演示SVD用于PCA降维的计算%matplotlib inline
%config InlineBackend.figure_format = 'svg'
import numpy as np
from sklearn.decomposition import PCAfrom matplotlib import pyplot as plt
from skimage import dataX = np.array([[-1.0, -3, -2], [-2, -1, -3], [-3, -2, -5], [2, 1, 3], [6, 1, 3], [2, 2, 3]])pca = PCA(n_components= 2)
X_new = pca.fit_transform(X)
print("\ndecomposition by pca:")
print("singular value:")
print(pca.singular_values_)
print("X_new:")
print(X_new)print("\ndecomposition by svd:")
U,S,Vt = np.linalg.svd(X-X.mean(axis = 0))
print("singular value:\n",S[:2])
print("X_new:")
print(np.dot(X-X.mean(axis = 0),np.transpose(Vt)[:,0:2]))# 注：降维结果中正负号的差异是因为PCA调整了SVD分解后的U和Vt符号以保持各列最大值取正
输出如下：
decomposition by pca:
singular value:
[11.31375337 2.89544001]
X_new:
[[ 3.23378083 1.06346839][ 3.88607412 -0.50763321][ 6.25267378 0.08479886][-3.50509914 -0.96584476][-6.02398361 1.89494314][-3.84344598 -1.56973242]]decomposition by svd:
singular value:[11.31375337 2.89544001]
X_new:
[[-3.23378083 -1.06346839][-3.88607412 0.50763321][-6.25267378 -0.08479886][ 3.50509914 0.96584476][ 6.02398361 -1.89494314][ 3.84344598 1.56973242]]下载1：OpenCV-Contrib扩展模块中文版教程
在「小白学视觉」公众号后台回复：扩展模块中文教程，即可下载全网第一份OpenCV扩展模块教程中文版，涵盖扩展模块安装、SFM算法、立体视觉、目标跟踪、生物视觉、超分辨率处理等二十多章内容。
下载2：Python视觉实战项目52讲
在「小白学视觉」公众号后台回复：Python视觉实战项目，即可下载包括图像分割、口罩检测、车道线检测、车辆计数、添加眼线、车牌识别、字符识别、情绪检测、文本内容提取、面部识别等31个视觉实战项目，助力快速学校计算机视觉。
下载3：OpenCV实战项目20讲
在「小白学视觉」公众号后台回复：OpenCV实战项目20讲，即可下载含有20个基于OpenCV实现20个实战项目，实现OpenCV学习进阶。
交流群
欢迎加入公众号读者群一起和同行交流，目前有SLAM、三维视觉、传感器、自动驾驶、计算摄影、检测、分割、识别、医学影像、GAN、算法竞赛等微信群（以后会逐渐细分），请扫描下面微信号加群，备注：”昵称+学校/公司+研究方向“，例如：”张三 + 上海交大 + 视觉SLAM“。请按照格式备注，否则不予通过。添加成功后会根据研究方向邀请进入相关微信群。请勿在群内发送广告，否则会请出群，谢谢理解~
