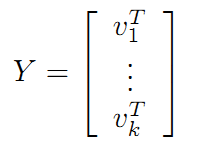SVD分解在很多经典应用中都有用到,比如数据压缩,降噪等,PCA也和SVD有着紧密联系,这里记录自己关于SVD分解求解最小二乘解的学习笔记,若有错误请指出,谢谢。
在实践中,由于存在测量误差和多次测量,所以超定方程是很常见的,所谓的超定方程是方程个数多于未知数个数的方程组,而对于线性方程组来说可能有解也有可能无解,如果没有解就不解了吗,不是的,我们还是要求必须解出来的,即使结果是个非精确的解,而这个解叫做线性最小二乘解。线性方程组分为两种,如下:
- 非齐次方程(Ax=b)的最小二乘解求解方法
- 正规方程求解
- 乔姆斯基分解法求解
- QR分解法求解
- 奇异值分解法求解(SVD)
- 齐次方程(Ax=0)的最小二乘解求解方法
1.线性空间
线性空间的属性:
- 维数:n
- 基:一组 n 个线性无关的向量
线性空间需要满足的条件:
-
加法封闭(可加性):空间内任意两向量相加(减),结果必须还在空间中。

-
数乘封闭(齐次性):空间内任意向量乘以标量,结果必须还在空间中。
![]()
注意:“数乘封闭”隐含了: 线性空间必须包括零向量(当 λ=0时);
2.矩阵4个子空间
首先,介绍下矩阵的秩(rank),即矩阵最大线性无关组中包含的向量数 ——刨除所有对张成的空间“毫无贡献”的向量(即线性相关的)后,剩下的有效向量数目。
假设 A 是 m×n 的矩阵,其秩为 r :
-
行空间(row space)
A 中所有行向量张成的子空间,维度是 r,记作:

-
列空间(column space)
A 中所有列向量张成的子空间,维度是 r,记作:

-
零空间(nullspace)
以 A 为系数矩阵的齐次线性方程组的所有非平凡解集张成的子空间,说人话就是“能令 Av = 0 的所有非零 v”:
![]()
-
左零空间(left nullspace)
类似列空间和行空间的关系,左零空间是 A 的转置的零空间;“左零”的说法来自其定义中矩阵是“左乘”到向量上的,而不是习惯上的右乘:

注意:
- 矩阵非奇异(可逆)的充分必要条件是矩阵的行、列数都等于秩,即满秩矩阵
- 无论是行向量之间,还是列向量之间,都线性无关,即矩阵中的每一行都为行空间贡献了维度,每一列都为列空间贡献了维度。
- 非奇异矩阵的零空间和左零空间就成了零维的,即其中只包含零向量
3.四个基本子空间的关系

对于线性变换:
![]()
这个变换的过程中:
- 向量 x 来自 A 的行空间或零空间(左侧的两个空间),变化后到达列空间。
按照矩阵乘法的定义,b是 A 中各列按照 x 的线性组合(或者说以 A 中各列为基,x 的坐标表示)。

- 对于非奇异矩阵 A(m*n),因为它是满秩的,行空间足以张成整个 Rn空间,列空间足以张成整个 Rm空间,那么行空间中所有向量一定可以一一映射到列空间中,行空间中零向量也只映射到列空间的零向量上。
- 对于奇异矩阵A(m*n),因为行空间中存在浑水摸鱼的向量(线性相关),其只能张成 r 维空间(r<n),剩下的 n−r维构成了零空间,零空间中的向量可能不是零,但在 A的线性变换作用下却映射到列空间的零向量上,即方程说的 Ax=0的非平凡(x不为 0 的)解。也就是说,零空间中的任何向量,和 A的任何一个行向量的内积都是 0
5.SVD分解
首先,对于A(mxn, m>n),其中秩r为:
![]()
A的行空间的一组正交基为:
![]()
A的 列空间的一组正交基为:
![]()
行空间和列空间之间满足关系:
![]()
对于奇异矩阵,剩下的n-r维就构成了零空间,使得Avi=0:
![]()
同样,ui扩展到Rm维空间

则可以得到:


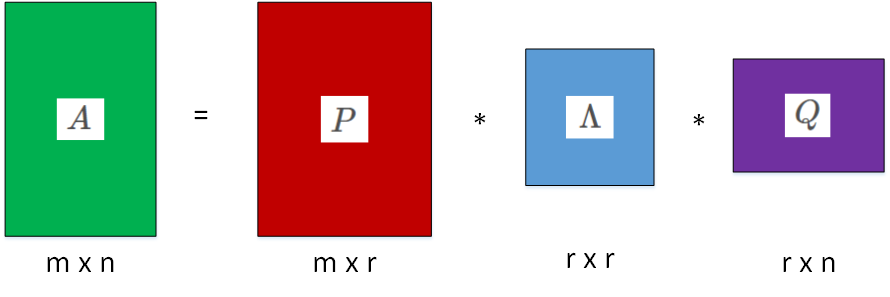
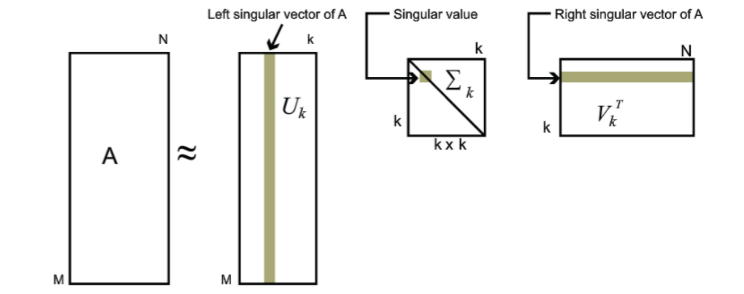
这样就可以得到A的奇异值分解:

其中,V是nxn的正交矩阵,U是mxm的正交矩阵,∑为mxn的对角矩阵。
6.SVD证明
首先,已知∑是mxn对角矩阵
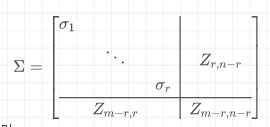
其中, 表示零矩阵(Zero matrix).
利用分块矩阵:

因为 是正交矩阵, 所以
![]()
7.SVD求解过程
- 求出方阵A^T*A和A*A^T

注意:
- 两个矩阵拥有完全相同的r个非0特征值。
- AAT和ATA都是对称矩阵

- 对A^TA进行特征分解得到特征值和特征向量满足下式
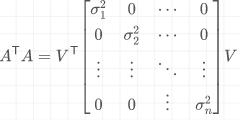
- 对AA^T进行特征分解得到特征值和特征向量满足下式

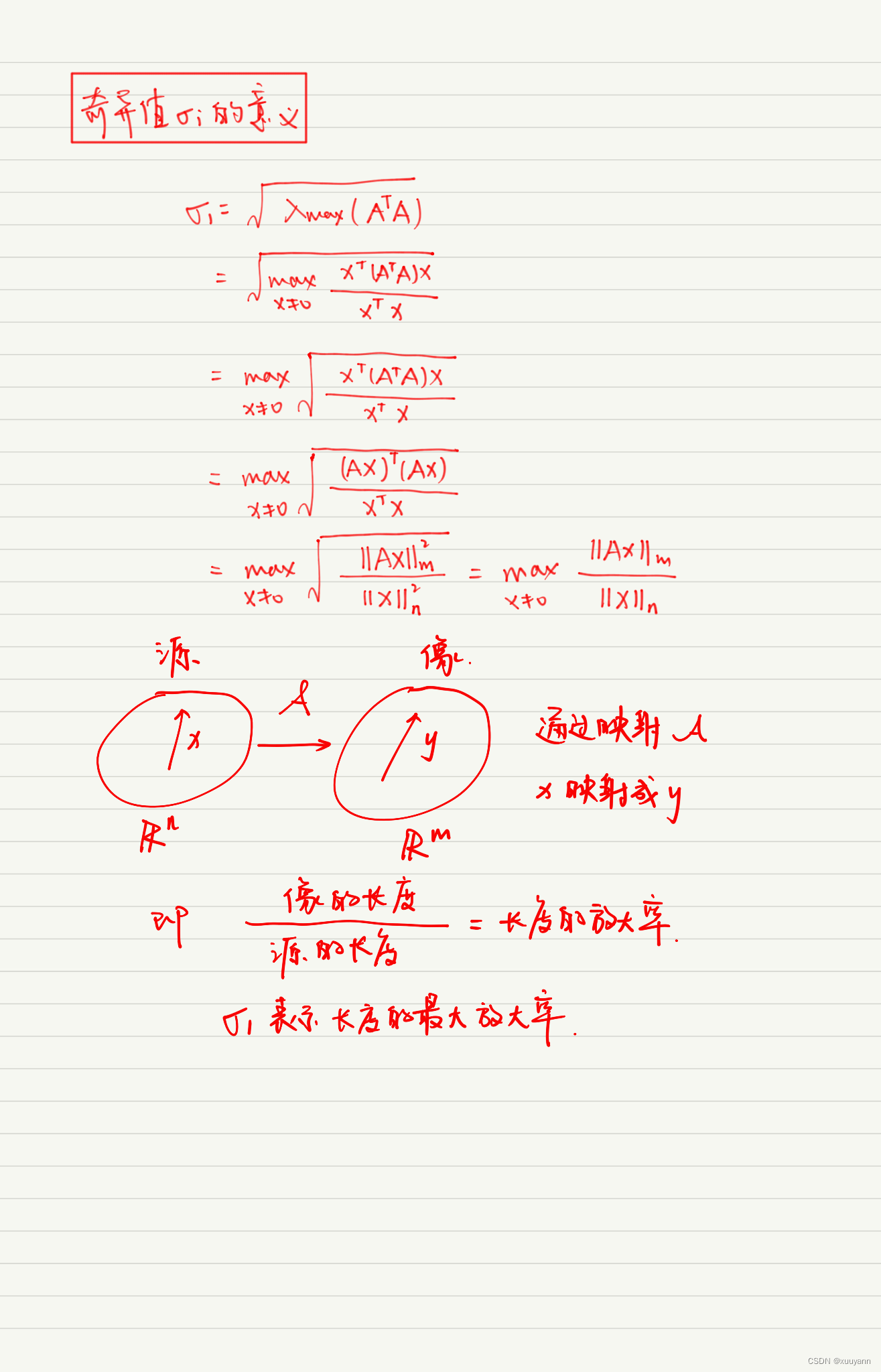
- 求出奇异值
![]()
- 得到A的奇异值分解
![]()
8.SVD求解 AX=b方程

9.SVD求解AX=0方程
目标:期望找到方程Ax = 0中 x 不等于零的解
由于该方程的特殊形式我们会发现对于 x 不等于零的解我们乘上任意的尺度因子 k 使解变为 kx 都不会改变最终结果。因为我们可以将问题转化为求解 x 使得||Ax||值最小并且||x||=1。




参考:
- 矩阵的四个基础子空间
-
奇异值分解(SVD)原理详解及推导
-
证明Ax=0的最小二乘解是ATA的最小特征值对应的特征向量(||x||=1)
-
SLAM中的优化理论(一)—— 线性最小二乘