矩阵分解

矩阵分解(decomposition,factorization)：将矩阵拆分为多个矩阵的乘积的运算。矩阵的分解包括以下几种：

• 特征分解
• SVD分解
• PCA
• QR分解
• LU分解
• 极分解

矩阵分解在数据压缩、推荐系统以及NLP等都有着比较广泛的应用。

特征分解

特征分解(eigendecomposition)：能够将矩阵分解成一组特征向量和特征值，是一种使用最为广泛的矩阵分解。并不是所有的矩阵能够使用矩阵分解，只有方阵(矩阵的行数等于列数)才有特征分解，我们可以使用下面的数学形式来表示特征分解：
$$Av=\lambda v$$
上面的式子中，非零向量$v$是矩阵$A$的特征向量，标量$\lambda$是特征向量$v$的特征值

• 特征分解究竟有何作用？
  通过特征分解我们能够将一个矩阵分解成为下面的形式：
  $$A=Q\Lambda Q^{-1}$$
  上式中的，$Q$是矩阵$A$的特征向量组成的正交矩阵，$\Lambda$是一个对角矩阵，每一个对角线元素就是一个特征值，特征值${\Lambda }_{i,i}$对应的特征向量是矩阵$Q$的第$i$列，特征值得大小表示对应特征向量对矩阵的重要程度
  
  通过特征分解后，我们就能分析出矩阵中特征向量的重要程度，通过分析特征向量对应特征的大小来判断特征向量的重要性，特征值越大表示特征向量越重要。

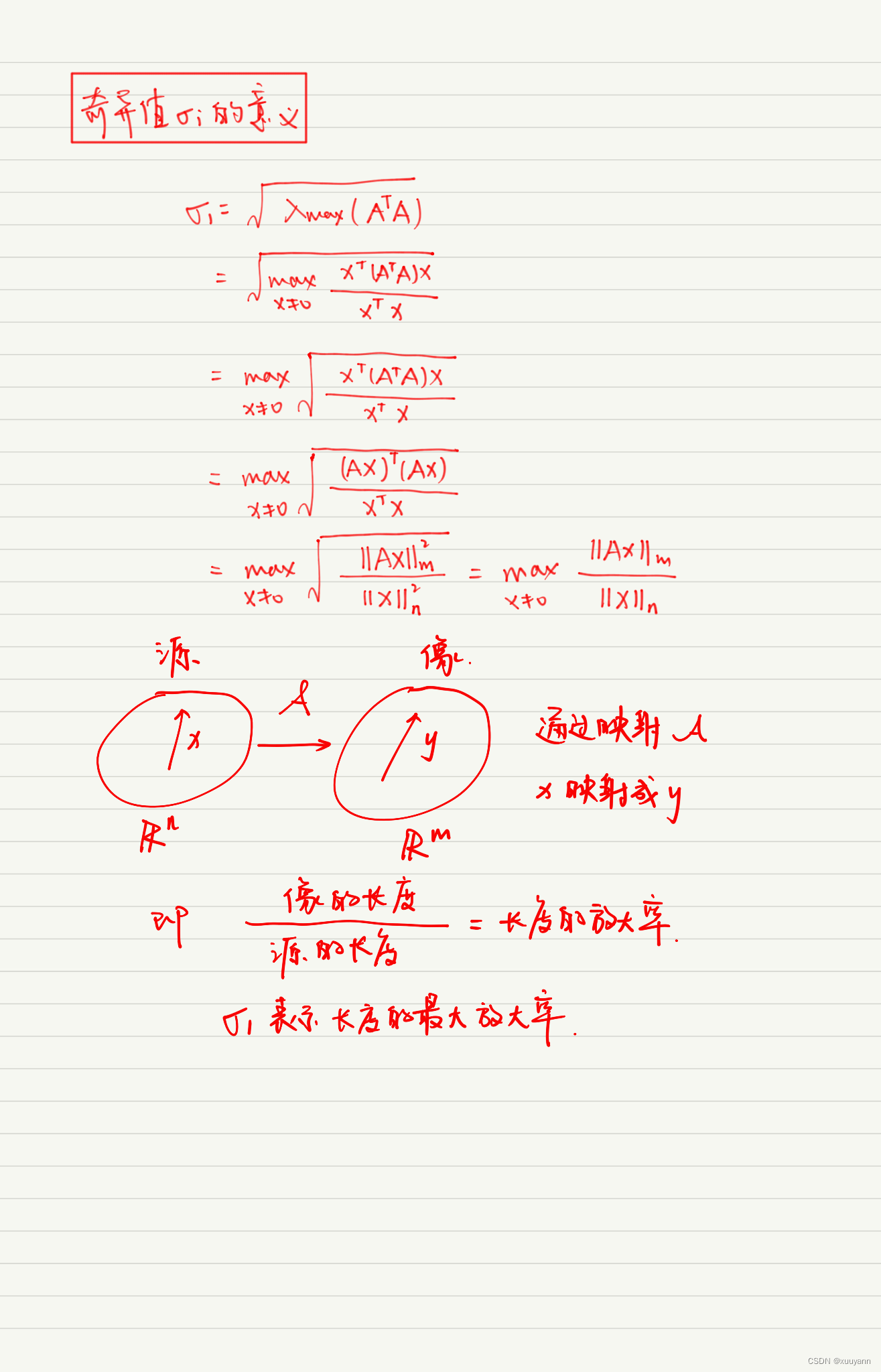
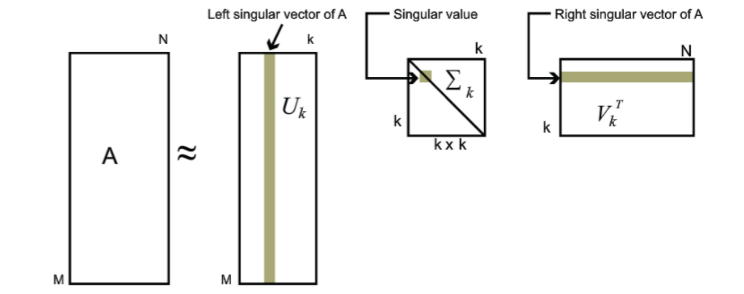
奇异值分解

奇异值分解(singular value decomposition,SVD)：将矩阵分解为奇异向量(singular vector)和奇异值(singular value)，奇异值分解得到的信息和特征分解得到信息是同类型的，相对特征分解来说奇异值分解的应用更为广泛，因为每个实数矩阵都有一个奇异值分解，但不一定有特征分解。因为只有方阵才有特征分解，对于非方阵我们就可以使用奇异值分解。

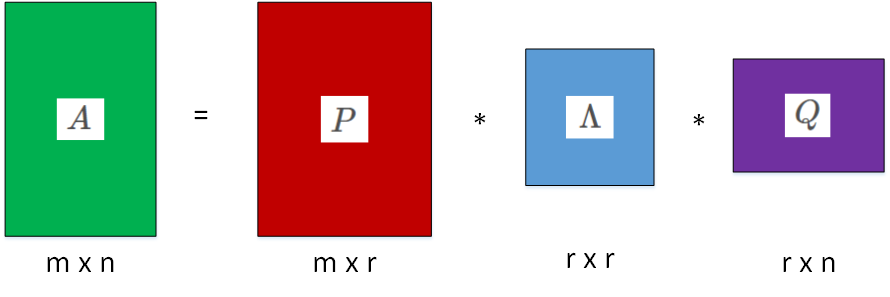
通过奇异值分解，我们可以将矩阵分解成为下面的形式：
$$A=UD{V}^T$$
如果$A$是一个$m\times n$的矩阵，那么$U$就是一个$m\times m$的矩阵，$D$就是一个$m\times n$的矩阵，$V$是一个$n\times n$的矩阵。

矩阵$U$和$V$是正交矩阵，而矩阵$D$是对角矩阵，矩阵$D$对角线上的元素称为矩阵$A$的奇异值。矩阵$U$的列向量称为左奇异向量(left singular vector)，矩阵$V$的列向量称为右奇异向量(right singular vector)

我们可以利用特征分解去解释矩阵的奇异值分解，$A$的左奇异向量是$A{A}^T$的特征向量，$A$的右奇异向量是$A^{T}A$的特征向量。$A$的非零奇异值是$A{A}^T$特征值的平方根，同时也是$A^{T}A$特征值的平方根。

除此之外，SVD还可以应用到矩阵求逆到非方阵上来。

伪逆

当我们需要求解一个线性方程的时候：
$$Ax=y$$
我们可以在等式的左边同时乘以矩阵$A$的逆矩阵$B$后，就可以得到
$$x=By$$
这样我们就能够求解线性方程的解。但是，如果矩阵$A$是非方阵，那么它就没有逆矩阵。这时候就只能通过Moore-Penrose 伪逆来解决这一类问题，矩阵$A$的伪逆的公式如下：
$$A^{+}=V{D}^{+}{U}^T$$
上式中的矩阵$U、D、V$是由矩阵$A$通过奇异值分解之后得到的矩阵，对角矩阵$D$的伪逆$D^{+}$是其非零元素取倒数之后再转置得到的。

当矩阵$A$的列数多于行数(未知数的个数大于方程个数)时，使用伪逆求解的线性方程可能是众多解法中的一种。当矩阵$A$的行数多于列数(方程的个数大于未知数的个数)时，方程可能没有解，在这种情况下，通过伪逆得到的$x$使得$Ax$和$y$的欧几里得距离$||Ax-y|{|}_2$最小。

特征分解和奇异值分解的示例

我们可以利用numpy中实现的特征分解和奇异值分解来测试一下

• 特征分解

import numpy as npa = np.array([[1,2,3],[4,5,6],[7,8,9]])
#w是特征值,v是特征向量
w,v = np.linalg.eig(a)
print(w)
print(v)
#w[i]对应的特征向量是v[:,i]
print(w[0])
print(v[:,0])
[ 1.61168440e+01 -1.11684397e+00 -1.30367773e-15]
[[-0.23197069 -0.78583024  0.40824829][-0.52532209 -0.08675134 -0.81649658][-0.8186735   0.61232756  0.40824829]]
16.116843969807043
[-0.23197069 -0.52532209 -0.8186735 ]

通过对矩阵做特征分解能够很容易通过特征值去判断那些特征向量对矩阵更重要

• SVD分解

import numpy as npa = np.array([[1,2,3,4],[4,5,6,7],[7,8,9,10]])
#SVD奇异值分解
#u左奇异向量矩阵,s奇异值矩阵,vh右奇异向量矩阵
u,s,vh = np.linalg.svd(a)
print(u.shape,s.shape,vh.shape)
#(3, 3) (3,) (4, 4)
print(s)
#[2.11562535e+01 1.55336357e+00 9.06493304e-17]#通过奇异值向量和奇异值还原矩阵
smat = np.zeros((u.shape[1], vh.shape[0]))
smat[:s.shape[0], :s.shape[0]] = np.diag(s)
restore_a = np.dot(np.dot(u,smat),vh)
# print(restore_a)#重构矩阵
num = 2
re_a = np.dot(np.dot(u[:,:num],np.diag(s[:num])),vh[:num,:])
print(re_a)
"""
[[ 1.  2.  3.  4.][ 4.  5.  6.  7.][ 7.  8.  9. 10.]]
"""

利用numpy我们能够很容易的来实现矩阵的奇异值分解，然后我们也利用了奇异值向量和奇异值来还原矩阵。

最后，我们发现我们再重建矩阵的时候只利用两个奇异值和奇异向量也能够完全的还原出原始矩阵，主要是因为第三个奇异值非常的小，对整个矩阵几乎没有影响。

在奇异值矩阵$D$中，是按照奇异值从大到小排列的，而且矩阵中的奇异值衰减的特别快。在很多情况下，前10%甚至前1%的奇异值之和就占了奇异值之和99%以上。也就是说，我们可以用前r(r远远小于m、n)个奇异值和奇异向量来近似描述矩阵。