SVD（奇异值分解）

article/2025/9/26 22:23:53

一、SVD（奇异值分解 Singular Value Decomposition）

1.1、基本概念：

（1）定义：提取信息的方法：奇异值分解Singular Value Decomposition（SVD）

（2）优点：简化数据， 去除噪声，提高算法的结果

（3）缺点：数据转换难以想象，耗时，损失特征

（4）适用于：数值型数据

1.2、原理–矩阵分解

将原始的数据集矩阵data(mn)分解成三个矩阵U(mn), Sigma(nm), VT(mn):
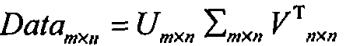
在这里插入图片描述
对于Sigma矩阵:

  • 该矩阵只用对角元素，其他元素均为零
  • 对角元素从大到小排列。这些对角元素称为奇异值，它们对应了原始数据集矩阵的奇异值
  • 这里的奇异值就是矩阵Data * DataT特征值的平方根。
  • 在某个奇异值的数目(r个 )之后，其他的奇异值都置为0。这就意味着数据集中仅有r个重要特征，而其余特征则都是噪声或冗余特征。
    • 确认r——启发式策略
    • 保留矩阵中90%的能量信息，将奇异值平方和累加加到90%
    • 若有上万奇异值，则保留2-3k

1.2.1、利用python实现svd

注意： sigma是返回行向量形式，只返回对角线元素， 这是Numpy的内部机制，为了节省空间

def loadExData():return[[0, 0, 0, 2, 2],[0, 0, 0, 3, 3],[0, 0, 0, 1, 1],[1, 1, 1, 0, 0],[2, 2, 2, 0, 0],[5, 5, 5, 0, 0],[1, 1, 1, 0, 0]]if __name__ == '__main__':print('============测试==============')U, Sigma, VT = linalg.svd(loadExData())print(U)print(Sigma)print(VT)U: [[-2.22044605e-16  5.34522484e-01  8.41650989e-01  5.59998398e-02	-5.26625636e-02  2.77555756e-17  1.38777878e-17][ 0.00000000e+00  8.01783726e-01 -4.76944344e-01 -2.09235996e-01	2.93065263e-01 -4.01696905e-17 -2.77555756e-17][ 0.00000000e+00  2.67261242e-01 -2.52468946e-01  5.15708308e-01	-7.73870662e-01  1.54770403e-16  0.00000000e+00][-1.79605302e-01  0.00000000e+00  7.39748546e-03 -3.03901436e-01	-2.04933639e-01  8.94308074e-01 -1.83156768e-01][-3.59210604e-01  0.00000000e+00  1.47949709e-02 -6.07802873e-01	-4.09867278e-01 -4.47451355e-01 -3.64856984e-01][-8.98026510e-01  0.00000000e+00 -8.87698255e-03  3.64681724e-01	2.45920367e-01 -1.07974660e-16 -1.12074131e-17][-1.79605302e-01  0.00000000e+00  7.39748546e-03 -3.03901436e-01	-2.04933639e-01  5.94635264e-04  9.12870736e-01]]# 注意： sigma是返回行向量形式，只返回对角线元素， 这是Numpy的内部机制，为了节省空间
Sigma: [9.64365076e+00 5.29150262e+00 7.40623935e-16 4.05103551e-16	2.21838243e-32]VT: [[-5.77350269e-01 -5.77350269e-01 -5.77350269e-01  0.00000000e+00	0.00000000e+00][-2.46566547e-16  1.23283273e-16  1.23283273e-16  7.07106781e-01	7.07106781e-01][-7.83779232e-01  5.90050124e-01  1.93729108e-01 -2.77555756e-16	-2.22044605e-16][-2.28816045e-01 -5.64364703e-01  7.93180748e-01  1.11022302e-16	-1.11022302e-16][ 0.00000000e+00  0.00000000e+00  0.00000000e+00 -7.07106781e-01	7.07106781e-01]]

Sigma的后三个值数量级非常小，所以将后三个值去掉

Sigma: [9.64365076e+00 5.29150262e+00 7.40623935e-16 4.05103551e-16	2.21838243e-32]

那么源数据Data可以使用下面结果近似计算：
   Datam*n = Um*2 * Sigma2*2 * VT2*n

在这里插入图片描述
重构矩阵：

    Sig2 = mat([[Sigma[0], 0],[0, Sigma[1]]])print(U[:, :2]*Sig2*VT[:2, :])[[ 5.38896529e-16  1.58498979e-15  1.58498979e-15  2.00000000e+00	2.00000000e+00][-1.04609326e-15  5.23046632e-16  5.23046632e-16  3.00000000e+00	3.00000000e+00][-3.48697754e-16  1.74348877e-16  1.74348877e-16  1.00000000e+00	1.00000000e+00][ 1.00000000e+00  1.00000000e+00  1.00000000e+00  0.00000000e+00	0.00000000e+00][ 2.00000000e+00  2.00000000e+00  2.00000000e+00  0.00000000e+00	0.00000000e+00][ 5.00000000e+00  5.00000000e+00  5.00000000e+00  0.00000000e+00	0.00000000e+00][ 1.00000000e+00  1.00000000e+00  1.00000000e+00  0.00000000e+00	0.00000000e+00]]

二、应用：

2.1、信息检索：隐性语义索引/分析（LSI/LSA）

  • 在LSI中，一个矩阵是由文档和词语组成的。当我们在该矩阵上应用SVD时，就会构建出多个奇异值。这些奇异值代表了文档中的概念或主题，这一特点可以用于更高效的文档搜索。在词语拼写错误时，只基于词语存在与否的简单搜索方法会遇到问题。简单搜索的另一个问题就是同义词的使用。这就是说，当我们查找一个词时,其同义词所在的文档可能并不会匹配上。如果我们从上千篇相似的文档中抽取出概念，那么同义词就会映射为同一概念。

2.2、推荐系统

2.2.1、基于协同过滤的推荐引擎

  协同过滤是通过将用户和其他用户的数据进行对比来实现推荐的。

2.2.2、相似度计算

  • 1、欧式距离（0~1）：
    相似度 = 1/ (1 + 距离)

  • 2、皮尔逊相关系数(Pearson correlation):
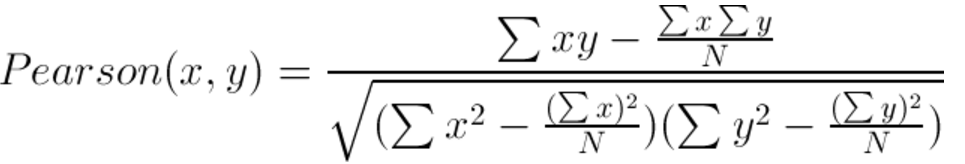
    　　　　在这里插入图片描述

    • 介绍
    • 该方法相对于欧氏距离的一个优势在于，它对用户评级的量级并不敏感。比如某个狂躁者对所有物品的评分都是5分，而另一个忧郁者对所有物品的评分都是1分，皮尔逊相关系数会认为这两个向量是相等的。
    • 皮尔逊相关系数的计算是由Numpy中的corrcoef()函数，他的取值范围在：(-1~1)
      后面我们很快就会用到它了。皮尔逊相关系数的取值范围从-1到+1，
    • 我们通过0.5 + 0 . 5 * corrcoef()把其取值范围归一化到0到 1之间。

  • 3、余弦相似度（cosine similarity）
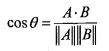
    　　　　在这里插入图片描述
    在这里插入图片描述
    其中，在Numpy中计算范数的公式：linalg.norm()
    相似度计算

def ecludSim(inA,inB):return 1.0/(1.0 + la.norm(inA - inB))def pearsSim(inA,inB):if len(inA) < 3 : return 1.0return 0.5+0.5*corrcoef(inA, inB, rowvar = 0)[0][1]def cosSim(inA,inB):num = float(inA.T*inB)# inA, inB 都是列向量denom = la.norm(inA)*la.norm(inB)return 0.5+0.5*(num/denom)print(ecludSim(mat1[:, 0], mat1[:, 3]))print(ecludSim(mat1[:, 0], mat1[:, 0]))print(pearsSim(mat1[:, 0], mat1[:, 3]))print(pearsSim(mat1[:, 0], mat1[:, 0]))print(cosSim(mat1[:, 0], mat1[:, 3]))print(cosSim(mat1[:, 0], mat1[:, 0]))

上面的相似度计算都是假设数据采用了列向量方式进行表示。如果利用上述函数来计算两个行向量的相似度就会遇到问题（我们很容易对上述函数进行修改以计算行向量之间的相似度)。这里采用列向量的表示方法，暗示着我们将利用基于物品的相似度计算方法。

2.2.3、基于物品的相似度还是基于用户的相似度？

行与行之间比较的是基于用户的相似度，列与列之间比较的则是基于物品的相似度。

  到底使用哪一种相似度呢？这取决于用户或物品的数目。基于物品相似度计算的时间会随物品数量的增加而增加，基于用户的相似度计算的时间则会随用户数量的增加而增加。如果我们有一个商店，那么最多会有几千件商品。在撰写本书之际，最大的商店大概有100 000件商品。而在Netflix大赛中，则会有480 000个用户和17 700部电影。如果用户的数目很多，那么我们可能倾向于使用基于物品相似度的计算方法。对于大部分产品导向的推荐引擎而言，用户的数量往往大于物品的数量，即购买商品的用户数会多于出售的商品种类。

2.2.4、推荐系统的评价

  • 采用交叉测试的方法。具体的做法就是，我们将某些已知的评分值去掉，然后对它们进行预测，最后计算预测值和真实值之间的差异。
  • 评价的指标是称为最小均方根误差（ RootMeanSquaredError, RMSE ) 的指标。
    • 它首先计算均方误差的平均值然后取其平方根。
    • 如果评级在1星到5星这个范围内，而我们得到的为1.0,那么就意味着我们的预测值和用户给出的真实评价相差了一个星级。

2.3、实例： 菜肴推荐

2.3.1、基于物的协同过滤算法

# 协同过滤算法
def standEst(dataMat, user, simMeas, item):'''协同过滤算法:param dataMat:  用户数据:param user:     用户:param simMeas:  相似度计算方法:param item:     物品:return: '''n = shape(dataMat)[1]  # 数据列数， 即物品的数量simTotal = 0.0;ratSimTotal = 0.0for j in range(n):userRating = dataMat[user, j]   # 用户评分if userRating == 0: continue    # 未进行打分# logical_and判断给定物品item与物品j评分重叠， 如果没有重叠就说明相似度为0# nonzero 第一个array表示非零元素所在的行，第二个array表示非零元素所在的列，分别取对应位置的值组成非零元素的坐标overLap = nonzero(logical_and(dataMat[:, item].A > 0, dataMat[:, j].A > 0))[0]if len(overLap) == 0:similarity = 0else:# 计算item与j的相似度similarity = simMeas(dataMat[overLap, item], dataMat[overLap, j])print('the %d and %d similarity is: %f' % (item, j, similarity))# 相似度的累加simTotal += similarity# 相似度评分累加ratSimTotal += similarity * userRating# 评分总和/相似度总和 对相似度评分总和进行归一化。 使得最后的评分在0~5之间if simTotal == 0:return 0else:return ratSimTotal / simTotal

2.3.2、推荐引擎

def recommend(dataMat, user, N=3, simMeas=cosSim, estMethod=standEst):'''推荐引擎:param dataMat:    用户数据:param user:       用户:param N:          评分最高的topN:param simMeas:    相似度计算方法:param estMethod:  估计方法：用于预测评分， 默认使用协同过滤算法:return: 	评分最高的topN'''# user 未评分的物品unratedItems = nonzero(dataMat[user, :].A == 0)[1]  # find unrated itemsif len(unratedItems) == 0: return 'you rated everything'itemScores = []# 对未评分的item遍历for item in unratedItems:# 估计的评分estimatedScore = estMethod(dataMat, user, simMeas, item)itemScores.append((item, estimatedScore))# 按照评分排序，返回评分最高的topNreturn sorted(itemScores, key=lambda jj: jj[1], reverse=True)[:N]if __name__ == '__main__':print('============测试==============')mat1 = mat(loadExData())mat1[0, 1] = mat1[0, 0] = mat1[1, 0] = mat1[2, 0] = 4mat1[3, 3] = 2print(mat1)print("recommend： ", recommend(mat1, 0))

2.3.3、利用SVD提高推荐

2.3.3.1、选择Sigma奇异值数量个数：

    # SVD分解U, Sigma, VT = linalg.svd(loadExData2())Sigma2 = Sigma**2# 保留矩阵中90%的能量信息，将奇异值平方和累加加到90%print(sum(Sigma2)*0.9, "~", sum(Sigma2))    # 487 ~ 541print(sum(Sigma2[:2]))  # 前两个奇异值能量和 378 < 487print(sum(Sigma2[:3]))  # 前三个奇异值能量盒 500 > 487, 所以选择前三个奇异值就可以了

2.3.3.2、基于SVD的估计方法

def svdEst(dataMat, user, simMeas, item):'''基于SVD实现的估计算法:param dataMat:  用户数据:param user:     用户:param simMeas:  相似度计算方法:param item:     物品:return: '''n = shape(dataMat)[1]simTotal = 0.0;ratSimTotal = 0.0# SVD 分解U, Sigma, VT = la.svd(dataMat)Sig4 = mat(eye(4) * Sigma[:4])  # arrange Sig4 into a diagonal matrix# 降维, 重构原矩阵xformedItems = dataMat.T * U[:, :4] * Sig4.I  # create transformed items# 估计评分for j in range(n):userRating = dataMat[user, j]if userRating == 0 or j == item: continuesimilarity = simMeas(xformedItems[item, :].T, \xformedItems[j, :].T)print('the %d and %d similarity is: %f' % (item, j, similarity))simTotal += similarityratSimTotal += similarity * userRatingif simTotal == 0:return 0else:# 归一化评分return ratSimTotal / simTotal

2.3.3.3、使用SVD实现推荐系统

    mat2 = mat(loadExData2())print("recommend： ", recommend(mat2, 4, estMethod=svdEst))

2.4、冷启动问题

  推荐引擎面临的另一个问题就是如何在缺乏数据时给出好的推荐。这称为冷启动问题，处理起来十分困难。

冷启动问题的解决方案，就是将推荐看成是搜索问题。在内部表现上，不同的解决办法虽然有所不同，但是对用户而言却都是透明的。为了将推荐看成是搜索问题，我们可能要使用所需要推荐物品的属性。在餐馆菜肴的例子中,我们可以通过各种标签来标记菜肴，比如素食、美式BBQ、价格很贵等。同时，我们也可以将这些属性作为相似度计算所需要的数据，这被称为基于内容(content-based)的推荐。可能，基于内容的推荐并不如我们前面介绍的基于协同过滤的推荐效果好 ，但我们拥有它，这就是个良好的开始。

三、总结： 此图借鉴于https://www.cnblogs.com/lesleysbw/p/6066444.html

在这里插入图片描述


http://chatgpt.dhexx.cn/article/pRFZjXj5.shtml

相关文章

SVD分解

SVD分解

一、SVD简介 Singular Value Decomposition&#xff08;奇异值分解&#xff0c;SVD&#xff09;是一种重要的矩阵分解技术&#xff0c;可以将一个矩阵分解为三个矩阵的乘积。SVD的应用广泛&#xff0c;包括数据降维、矩阵逆运算、推荐系统等领域。 给定一个矩阵A&#xff0c;SV…
阅读更多...
如何快速搭建个人网站（服务器配置篇）

如何快速搭建个人网站（服务器配置篇）

关于服务器的购买和域名注册可以参考我的这篇博客 在使用之前&#xff0c;建议小白用户先下载一个Vmware 安装一个Ubuntu的虚拟环境学习一下linux的基础命令。 一、远程服务器的连接 服务器购买好了以后我们需要进行远程连接我们的服务器&#xff0c; 我个人推荐windows用…
阅读更多...
在废旧手机里搭建个人服务器

在废旧手机里搭建个人服务器

点击跳转微信公众号原文链接 欢迎关注公众号&#xff0c;会不定时发些有趣的干货文章&#xff0c;以及一些记录性的技术文章&#xff01; 正文开始&#xff1a; 一、目的&#xff1a;给手机装上Linux系统&#xff0c;充当服务器使用 二、流程&#xff1a; 1、手机装好相关软件…
阅读更多...
个人搭建网站的服务器选择

个人搭建网站的服务器选择

关于这方面之前一直准备分享一下心得&#xff0c;由于一直比较忙&#xff0c;各种想写的就各种耽搁了&#xff0c;今天给大家总结一下个人或小型企业站该如何选择网站服务器 首先&#xff0c;先弄清楚自己的需求和用途&#xff1a; 1、是建立一个静态页面还是动态页面&#xff…
阅读更多...
如何利用云服务器搭建个人网站

如何利用云服务器搭建个人网站

去阿里云进入官网 aliyun.com 注册账号 小林同学在这里用阿里云演示&#xff0c;大家也可以去腾讯云、百度云注册等大型知名企业&#xff0c;步骤雷同&#xff0c;看个人喜欢 注册完&#xff0c;完善个人信息&#xff0c;进行实名认证 主页面 点击 最新活动 并找到 新手上路 和…
阅读更多...
【Linux】零成本在家搭建自己的私人服务器解决方案

【Linux】零成本在家搭建自己的私人服务器解决方案

我这个人自小时候以来就特喜欢永久且免费的东西&#xff0c;也因此被骗过&#xff08;花巨款买了永久超级会员最后就十几天&#xff09;。 长大后骨子里也是喜欢永久且免费的东西&#xff0c;所以我不买服务器&#xff0c;用GitHubPage或者GiteePage搭建自己的静态私人博客&…
阅读更多...
如何组装、搭建一台永久运行的个人服务器？

如何组装、搭建一台永久运行的个人服务器？

点击关注公众号&#xff0c;实用技术文章及时了解 来源&#xff1a;segmentfault.com/a/1190000021143144 一、前言 由于本人在这段时候&#xff0c;看到了一个叫做树莓派的东东&#xff0c;初步了解之后觉得很有意思&#xff0c;于是想把整个过程记录下来。 二、树莓派是什么&…
阅读更多...
完全免费快速搭建个人www服务器

完全免费快速搭建个人www服务器

想拥有自己的web服务器吗&#xff1f;想把服务器放到自己家里吗&#xff1f;通过ADSL拨号也能建立个人的服务器吗&#xff1f;本文告诉你答案。 要建立自己的web服务器&#xff0c;需要两个最重要的工作&#xff1a; 1 让别人知道你的主机 目前访问Internet上主机的方式主要有…
阅读更多...
用服务器建立个人网站

用服务器建立个人网站

首先&#xff0c;我们需要购买云服务器和域名。 域名建议用.com后缀的&#xff08;一般五十左右&#xff09;&#xff0c;想要便宜的域名可以买.top等后缀的&#xff08;一般几块钱&#xff09;。 点击这里购买域名 三丰云服务器的话&#xff0c;根据自己的需要购买&#xf…
阅读更多...
家庭宽带搭建个人服务器

家庭宽带搭建个人服务器

家庭宽带搭建个人服务器 家庭宽带搭建个人服务器准备1.公网IP1.1光猫改桥接模式 2.一台PC主机 安装PVE系统1.下载PVE镜像文件2.制作U盘启动盘 PVE安装Centos1.创建虚拟机2.启动虚拟机 完成centos安装步骤即可 域名解析实现公网访问1.测试公网连接 家庭宽带搭建个人服务器 想必…
阅读更多...
家用宽带搭建个人服务器（一）

家用宽带搭建个人服务器（一）

本文主要详记从 安装电信宽带 到使用动态公网IP 访问家里电脑的 web服务 写在前头 以前不知道在哪看过家用宽带搭建个人网站这种文章&#xff0c;所以心里一直对这个事念念不忘&#xff0c;毕竟万物皆可薅&#xff0c;能免费就免费&#xff0c;要用有限的生命好好折腾一番 1.…
阅读更多...
电脑搭建个人服务器

电脑搭建个人服务器

电脑搭建个人服务器 #一.准备工作二.设置Xampp三.安装宝塔面板 #一.准备工作 1.下载Xampp和kodbox.1.22 2.下载宝塔面板 二.设置Xampp 1.打开Xampp&#xff0c;找到安装路径下的&#xff0c;如图打开xampp-control.exe 2.打开页面 2.如果点击Apache的start开启不成功的话…
阅读更多...
搭建个人云服务器

搭建个人云服务器

创建新浪云计算应用 申请账号 我们使用SAE新浪云计算平台作为服务器资源&#xff0c;并且申请PHP环境MySQL数据库作为程序运行环境。申请地址为&#xff1a; 注册地址&#xff1a;http://www.sinacloud.com/public/login/inviter/gaimrn-mddmzeKWrhKWvrICun2Z_eIlnf6Kqdg.ht…
阅读更多...
【个人网站搭建】服务器、域名准备

【个人网站搭建】服务器、域名准备

【个人网站搭建】服务器、域名准备 用最简单的方式&#xff0c;带你上线自己的网站&#xff01;前言 建网站本身是一个很大的工程&#xff0c;涉及前端页面的搭建&#xff0c;网站数据的存储&#xff0c;还要购置服务器资源&#xff0c;域名等。我们要上线个人网站&#xff0…
阅读更多...
家用宽带搭建个人服务器（二）

家用宽带搭建个人服务器（二）

本文主要详记免费二级域名注册和免费DDNS解析 写在前头 近几年国内注册域名需要备案&#xff0c;域名解析服务商都陆续需要收费了&#xff0c;对于我这种想简单玩玩的人来说实在是太麻烦了(主要是费钱&#xff09;&#xff0c;花了点时间找到了免费域名注册和DDNS解析 本文基于…
阅读更多...
【VMware】搭建个人服务器

【VMware】搭建个人服务器

文章目录 准备工作三种网络模式Bridged(桥接模式)定义设置 NAT(网络地址转换模式)定义设置 Host-Only(仅主机模式)定义设置 搭建服务器网络模式的选择在VMWare的网络编辑器中设置转发端口查看宿主机的ip地址使用ssh连接工具进行连接 Mac笔记本跑虚拟机总感觉别扭&#xff0c;通…
阅读更多...
阿里云服务器搭建个人网站

阿里云服务器搭建个人网站

文章目录 一、事先准备1、购买阿里云服务器2、购买域名,并进行备案 二、服务器的基本使用1、服务器配置2、远程连接 三、服务器的高级使用1、安装宝塔面板2、部署网站3、固定链接的设置4、为网站部署SSL证书(重点) 一、事先准备 1、购买阿里云服务器 https://www.aliyun.com/…
阅读更多...
服务器搭建个人网站（阿里云服务器）

服务器搭建个人网站（阿里云服务器）

服务器搭建个人网站 一丶购买服务器 这里我选的是阿里云服务器&#xff0c;进入阿里云官网阿里云-上云就上阿里云 阿里云提供了几种服务器&#xff0c;云服务器ESC、轻量应用服务器&#xff0c;ESC更好一点儿&#xff0c;我选了轻量级应用服务器。购买好了之后&#xff0c;在…
阅读更多...
搭建个人服务器

搭建个人服务器

组建一个自己的服务器 一、服务器是什么&#xff1f;他的作用是什么&#xff1f;二、服务的分类&#xff01;三、域名是什么&#xff1f; 相信学习了一段时间的网页以后&#xff0c;都想自己做一个网站&#xff0c;体验一哈当站长的感觉&#xff0c;这里小佬弟今天就教大家搭建…
阅读更多...
手把手教你搭建一台永久运行的个人服务器

手把手教你搭建一台永久运行的个人服务器

No.1 树莓派是什么&#xff1f; 1. 用我的话理解2. 市面上的型号3. 树莓派 zero w4. 更多树莓派No.2 树莓派zero w安装系统 1. 准备2. 第一步下载系统镜像3. 使用 Win32DiskImager 往内存卡中写入镜像4. 修改 boot 分区的文件5. 组装我们的最小主机并连接6. 优化咱们树莓派的系…
阅读更多...
推荐文章

Copyright @ 2022~2023