前言

相对于Vivado与Quartus自带的编辑器，使用Sublime可以提高Verilog的编写效率。Sublime是可以自己编写插件并使用的，合理的运用插件可以提高开发Verilog生产力。

一、插件安装

1.打开Sublime，点击【Preferences】、【Package Control】，或快捷键ctrl+shift+P。
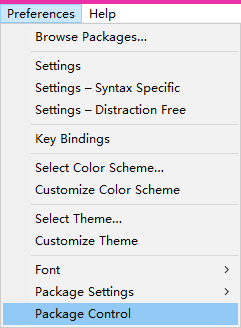
在这里插入图片描述
2.在弹出的终端窗口输入install，下方就会自动出现一些选项，选择Package Control:install package。

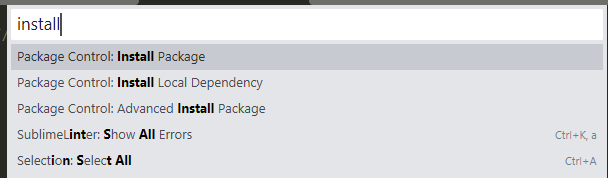
3.等待一段时间，就可以输入你想要的插件，搜索出后点击，就会自动安装插件了。
右下角有进度提示。在这里插入图片描述

二、插件推荐

1.SnippetMaker

SnippetMaker 插件提供 snippet 文件的快捷生成和打包操作，用于快速实现自定义代码块。
① 首先在编辑器中编写想要打包的代码块，并且选中。
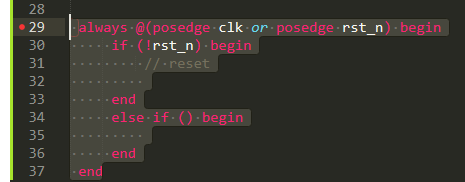
在这里插入图片描述
② 按 ctrl+shift+P ，并输入 make ，选择下图光标所示的选项。

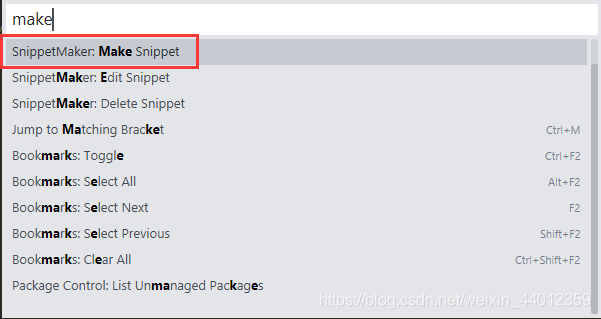
③ 在下方控制台中输入触发代码块的提示符，比如 “z” ，然后回车。
④ 再输入描述信息（随便写，描述一下代码块作用就行），回车。
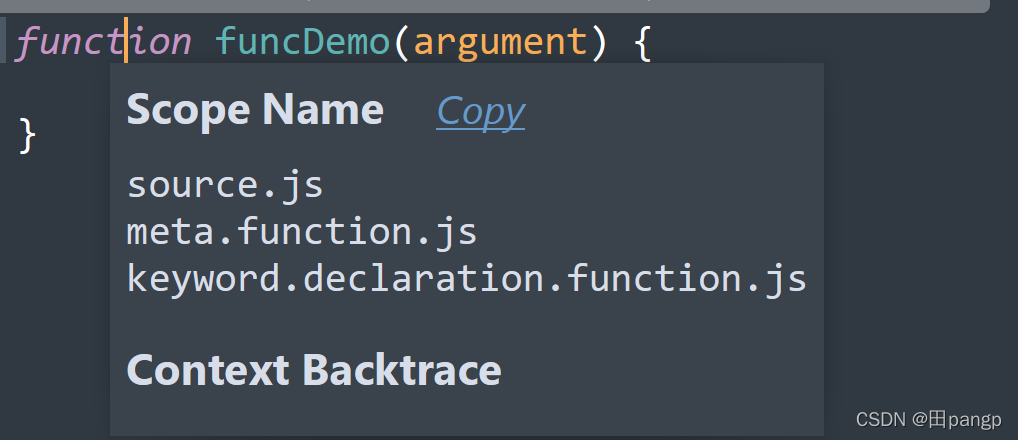
⑤ 出现 “source.verilog, keyword.control.verilog” 信息，直接回车。
⑥ 出现默认保存文件名 “z.sublime-snippet”，回车保存。
⑦ 在编辑器中输入 “z” 就能看见提示，按 Tab 键即可插入刚才编辑好的代码块。

如想删除保存的代码块，点击【Preferences】、【Browser Packages】。User文件夹内就是我们安装的插件，其中snippets文件夹内就是保存的代码块。

2.verilog Gadget

verilog Gadget插件提供了自动生成例化模板、自动生成tb模板（Systemverilog）、插头信息、对齐操作等操作。
① 在一个.v文件内右键并选择 Instantiate Module ，再在需要的地方粘贴就可以自动生成例化模板。
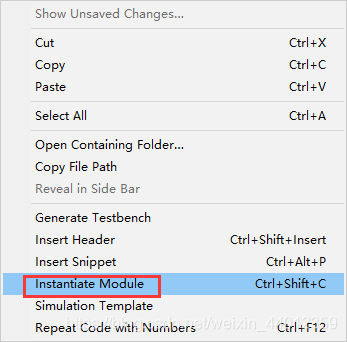
在这里插入图片描述
② 在一个.v文件内右键并选择 Simulation Template 就可自动打开tb模板，按ctrl+S保存。
③ 在一个.v文件内右键并选择 Insert Header 可插入头信息。
④ 按快捷键 ctrl+shift+x 可以代码对齐。
其他功能和快捷键请查阅插件中的 README 。

SublimeLinter-contrib-iverilog

SublimeLinter 是 sublime自带的语法检查插件，又在 SublimeLinter 的基础上开发了针对各种语言的语法检查插件。Verilog 语言相关的语法检查插件有 SublimeLinter-contrib-iverilog、SublimeLinter-contrib-verilator 和 SublimeLinter-contrib-modelsim。
sublime 通过调用第三方仿真器的语法检查器来对 sublime 内的 Verilog 代码进行语法检测。
iverilog(Icarus Verilog)是一款轻量级开源 Verilog 仿真器，安装空间很小，启动迅速调用方便，但对 systemverilog 支持不好。这里我安装了 iverilog ，并且选用 SublimeLinter-contrib-iverilog 插件。
① 安装 iverilog ，直接进入官网link. 下载就可以，安装过程全程** 勾选** 和 **确认 **。
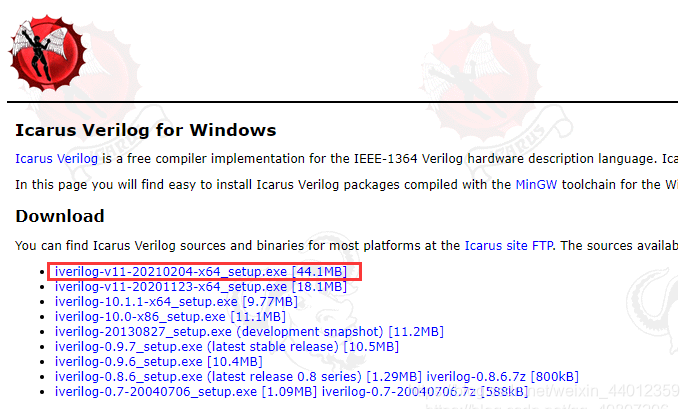
在这里插入图片描述
② 安装 SublimeLinter 插件。直接在 sublime 的 install packet 安装即可。
③ 安装完 SublimeLinter 后，再安装 SublimeLinter-contrib-iverilog 。
④ 在 sublime 界面点击 Preference(中文版: 首选项) -> package setting -> SublimeLinter -> setting ，然后在 User 界面的 { } 中写入如下代码，并且只需要改动 iverilog 的安装路径（如下，具体到bin文件夹），改完后保存。

"paths": {"linux": [],"osx": [],"windows": ["D:\\iverilog\\bin",],},"linters": {"iverilog": {"disable": false,"args": ["-i"], // add the "-i" flag"excludes": [],},},

⑤ 重启 sublime ，即可检查 Verilog 语法错误。