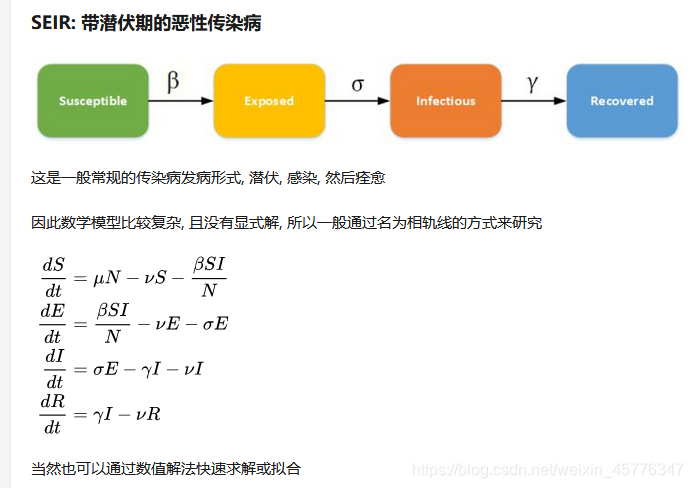
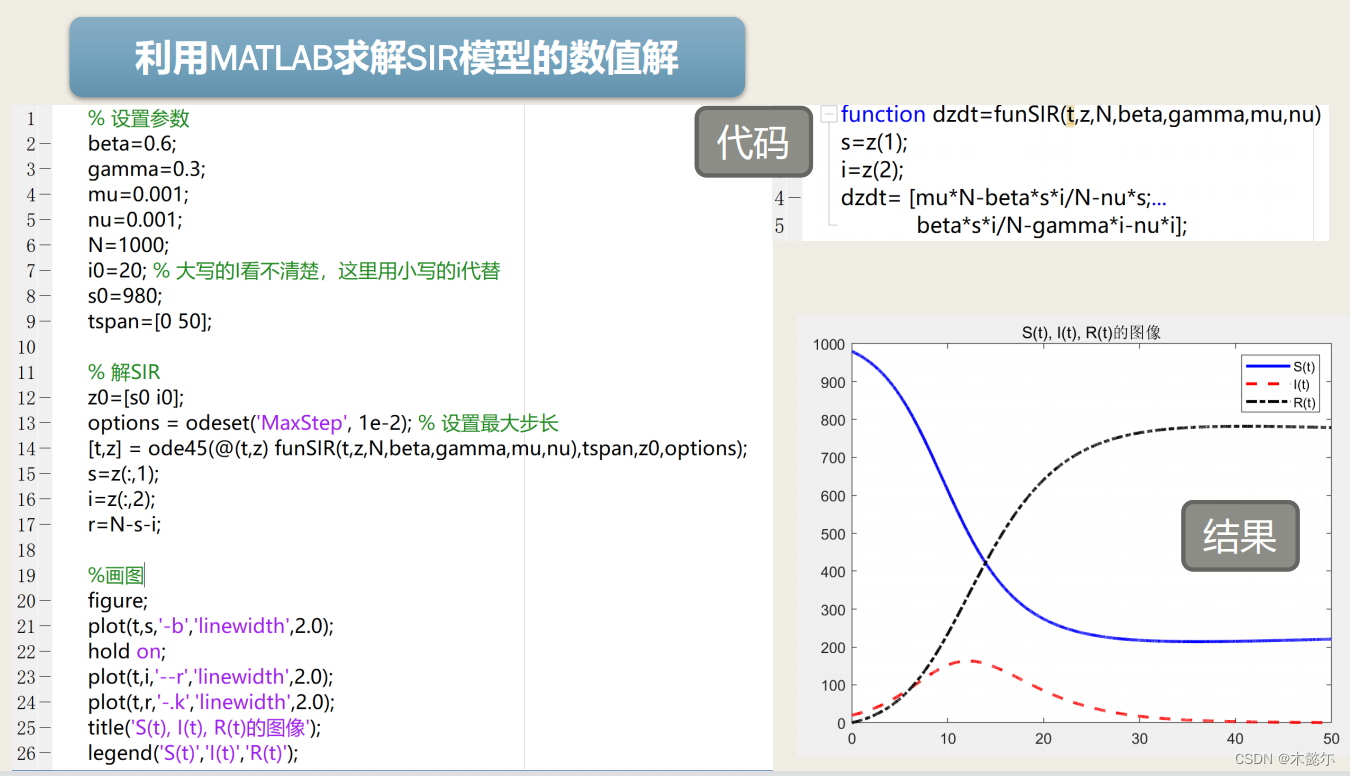
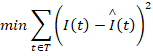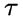SI模型

假设：

1）节点均匀混合

2）感染后染病状态不再改变

3）接触病原体后以一定概率感染：

4）初始状态的人群感染密度为：

则感染过程动力学方程为：

如果设初始感染密度为则感染密度随时间增长规律为：

特点：

1）感染密度随着时间指数上升直到趋近于全部感染

2）易感染密度下降到原来的（约36%）所需的特征时间为

采用sicpy数值求解动力学方程：

import numpy as np
import scipy.integrate as spi
import matplotlib.pyplot as plt
beta=0.4
avg_k=4
#动力学方程标准形式右侧函数定义
def si_diff(i,t):return beta*avg_k*i*(1-i)
i0=1e-6
t=np.arange(0,70,1)
i_t=spi.odeint(si_diff,i0,t)
s_t=1-i_t
fig,ax=plt.subplots(subplot_kw={'facecolor':"#ebf5ff"})
ax.plot(t,i_t,label="i(t)")
ax.plot(t,s_t,label="s(t)")
ax.set_xlabel("t")
ax.set_ylabel("%")
ax.legend()
plt.show()