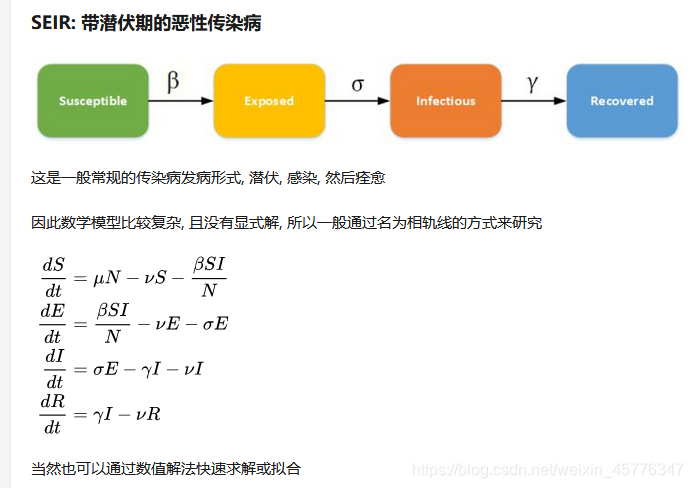
1. SEIR模型

适用于存在易感者、暴露者、患病者和康复者4类人群，有潜伏期、治愈后获得终身免疫的疾病，如带状疱疹、水痘。

模型假设

假设易感者与患病者有效接触即变为暴露者，暴露者经过平均潜伏期后成为患病者，患病者可被治愈成为康复者，康复者终身免疫不再易感；以一天作为模型的最小时间单元。

总人数为N，不考虑人口的出生与死亡，迁入与迁出，此总人数不变。

2. Demo1

N=330000000;
load America.mat
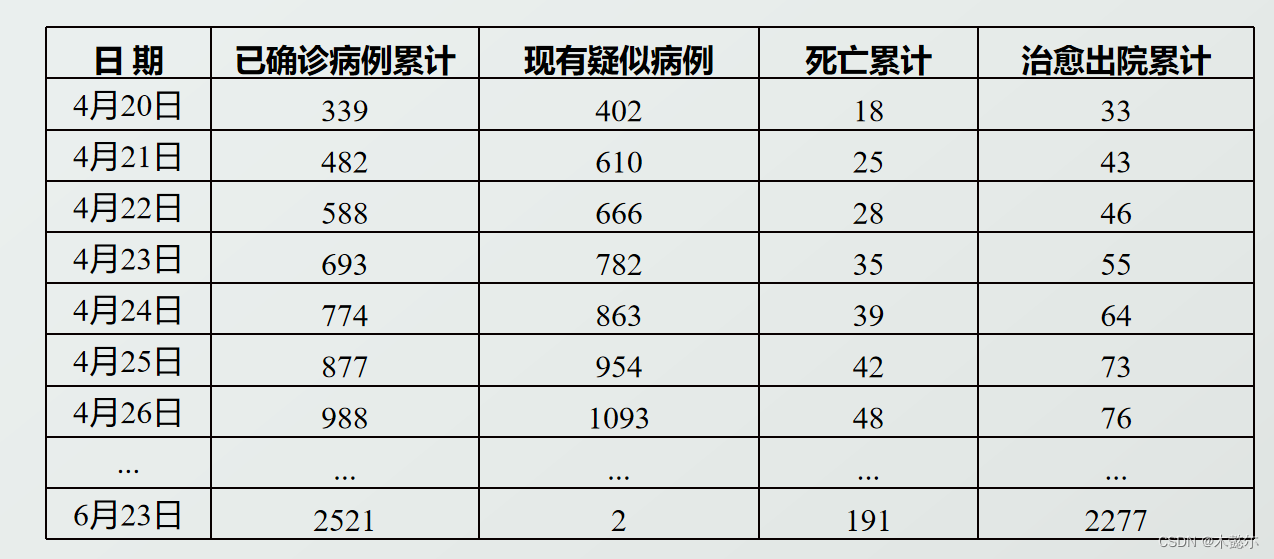
%第一列为累计确诊人数，第二列为累计死亡人数，第三列为累计治愈人数
E=0;%潜伏者
D=0;%死亡患者人数
I=1;%感染人数
S=N-I;%易感人数
R=0;%康复者人数
r=17;%感染者接触数量
% r=19;
B=0.602;%传染概率
% a=0.17;%潜伏者转化为感染者的概率
% a=0.175;
a=0.18;%潜伏者转化为感染者的概率
% r2=8;%潜伏者接触人数
r2=15;%潜伏者接触人数
% B2=0.03;%潜伏者传染正常人的概率
B2=0.05;
y=0.000316893;%康复概率
k=0.01;%日致死率
B3=0.001;%转阴率
%  T=1:200;
T=1:180;
for idx=1:length(T)-1%在政府发出管控号召时间以及各个地方响应延迟时间，此处采用11天后为临界点，%相当于11天后，感染者与潜伏者流动性和医疗配置发生明显变化，具体为接触人数if idx>=14r=0.20;%感染者接触数量r2=1.8;%感染者接触人数量y=0.15;%康复率上升a=0.12;%潜伏者转化为感染者的概率k=0.0001;%日致死率暂无改变endif idx<11S(idx+1)=S(idx)-r*B*S(idx)*I(idx)/N-r2*B2*S(idx)*E(idx)/N;%易感人群迭代E(idx+1)=E(idx)+r*B*S(idx)*I(idx)/N-a*E(idx)+r2*B2*S(idx)*E(idx)/N;%潜伏者迭代I(idx+1)=I(idx)+a*E(idx)-(k+y)*I(idx);%感染人数迭代R(idx+1)=R(idx)+0.05*I(idx);%康复人数迭代D(idx+1)=D(idx)+k*I(idx);%死亡患者人数迭代elseS(idx+1)=S(idx)-r*B*S(idx)*I(idx)/N-r2*B2*S(idx)*E(idx)/N+B3*E(idx-10);%易感人群迭代E(idx+1)=E(idx)+r*B*S(idx)*I(idx)/N-a*E(idx)+r2*B2*S(idx)*E(idx)/N-B3*E(idx-10);%潜伏者迭代I(idx+1)=I(idx)+a*E(idx)-(k+y)*I(idx);%感染人数迭代% Y参数有问题R(idx+1)=R(idx)+0.045*I(idx-9);%康复人数迭代D(idx+1)=D(idx)+k*I(idx);%死亡患者人数迭代end
end
B={'01-19','02-08','02-28','03-19','04-08','04-28','05-18','06-07','06-27','07-17','08-06'};
% plot(1:1:102,huibei(:,1)-huibei(:,2)-huibei(:,3),'r*');hold on
plot(1:1:133,America(:,1)-America(:,2)-America(:,3),'g');hold on
plot(1:1:133,America(:,3),'m');hold on
% legend('实际患病','实际康复')
% xlabel('天数');
% ylabel('人数');
% legend('实际患病')
plot(T,R,'b')
plot(T,I,'r')
% plot([7 7],[0 1000],'c')
plot(T,D,'k');
legend({'实际患病','实际康复','预测康复者','预测患者','死亡患者'},'Fontsize', 18);
grid on;
set(gca,'XTickLabel',B)
xlabel('日期');
ylabel('人数');
title('采取隔离措施的SEIR模型');

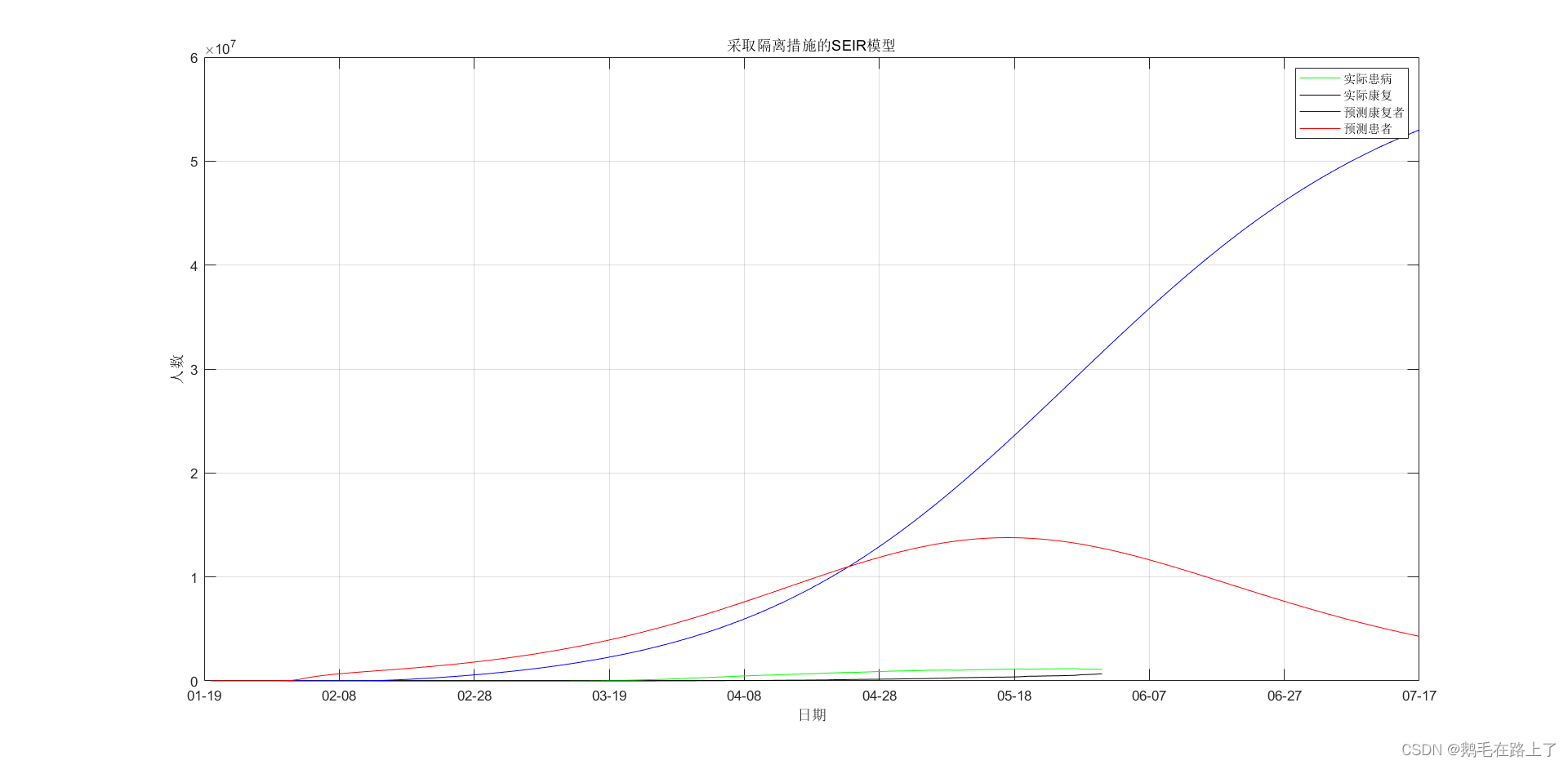
在这里插入图片描述

3. Demo2

%假设1月15日开始出现第一例确诊，；1月23号武汉政府开始封城，此时其他省市也相应作出响应隔离措施，大约距离15号后的11天政府管控发挥明显作用
%  N=13.95*100000000;%人口数N=1395380000;
load quanguo1.mat
%第一列为累计确诊人数，第二列为累计死亡人数，第三列为累计治愈人数
E=0;%潜伏者
D=0;%死亡患者人数
I=1;%感染人数
S=N-I;%易感人数
R=0;%康复者人数
r=17;%感染者接触数量
% r=19;
B=0.602;%传染概率
% a=0.17;%潜伏者转化为感染者的概率
% a=0.175;
a=0.298;%潜伏者转化为感染者的概率
% r2=8;  %潜伏者接触人数
r2=15;%潜伏者接触人数
% B2=0.03;%潜伏者传染正常人的概率
B2=0.05;
y=0.05;%康复概率
k=0.0001;%日致死率
B3=0.1;%转阴率
%  T=1:200;
T=1:180;
for idx=1:length(T)-1%若以1月18日为疫情起点，在政府发出管控号召时间以及各个地方响应延迟时间，此处采用11天后为临界点，%相当于11天后，感染者与潜伏者流动性和医疗配置发生明显变化，具体为接触人数if idx>=11r=0.20;%感染者接触数量r2=1.8;%感染者接触人数量y=0.15;%康复率上升a=0.12;%潜伏者转化为感染者的概率k=0.0001;%日致死率暂无改变endif idx<11S(idx+1)=S(idx)-r*B*S(idx)*I(idx)/N-r2*B2*S(idx)*E(idx)/N;%易感人群迭代E(idx+1)=E(idx)+r*B*S(idx)*I(idx)/N-a*E(idx)+r2*B2*S(idx)*E(idx)/N;%潜伏者迭代I(idx+1)=I(idx)+a*E(idx)-(k+y)*I(idx);%感染人数迭代R(idx+1)=R(idx)+0.05*I(idx);%康复人数迭代D(idx+1)=D(idx)+k*I(idx);%死亡患者人数迭代elseS(idx+1)=S(idx)-r*B*S(idx)*I(idx)/N-r2*B2*S(idx)*E(idx)/N+B3*E(idx-10);%易感人群迭代E(idx+1)=E(idx)+r*B*S(idx)*I(idx)/N-a*E(idx)+r2*B2*S(idx)*E(idx)/N-B3*E(idx-10);%潜伏者迭代I(idx+1)=I(idx)+a*E(idx)-(k+y)*I(idx);%感染人数迭代% Y参数有问题R(idx+1)=R(idx)+0.045*I(idx-9);%康复人数迭代D(idx+1)=D(idx)+k*I(idx);%死亡患者人数迭代end
end
B={'01-19','02-08','02-28','03-19','04-08','04-28','05-18','06-07','06-27','07-17','08-06'};
% plot(1:1:102,huibei(:,1)-huibei(:,2)-huibei(:,3),'r*');hold on
plot(1:1:137,quanguo1(:,1)-quanguo1(:,2)-quanguo1(:,3),'g-');hold on
plot(1:1:137,quanguo1(:,3),'m-');hold on
% legend('实际患病','实际康复')
% xlabel('天数');
% ylabel('人数');
% legend('实际患病')
plot(T,R,'b',T,I,'r',T,D,'k');
grid on;
hold on;
% plot([7 7],[0 1000]);
set(gca,'XTickLabel',B)
xlabel('日期');
ylabel('人数');
legend({'实际患病','实际康复','预测康复者','预测患者','死亡患者'},'Fontsize', 18);
title('采取隔离措施的SEIR模型');

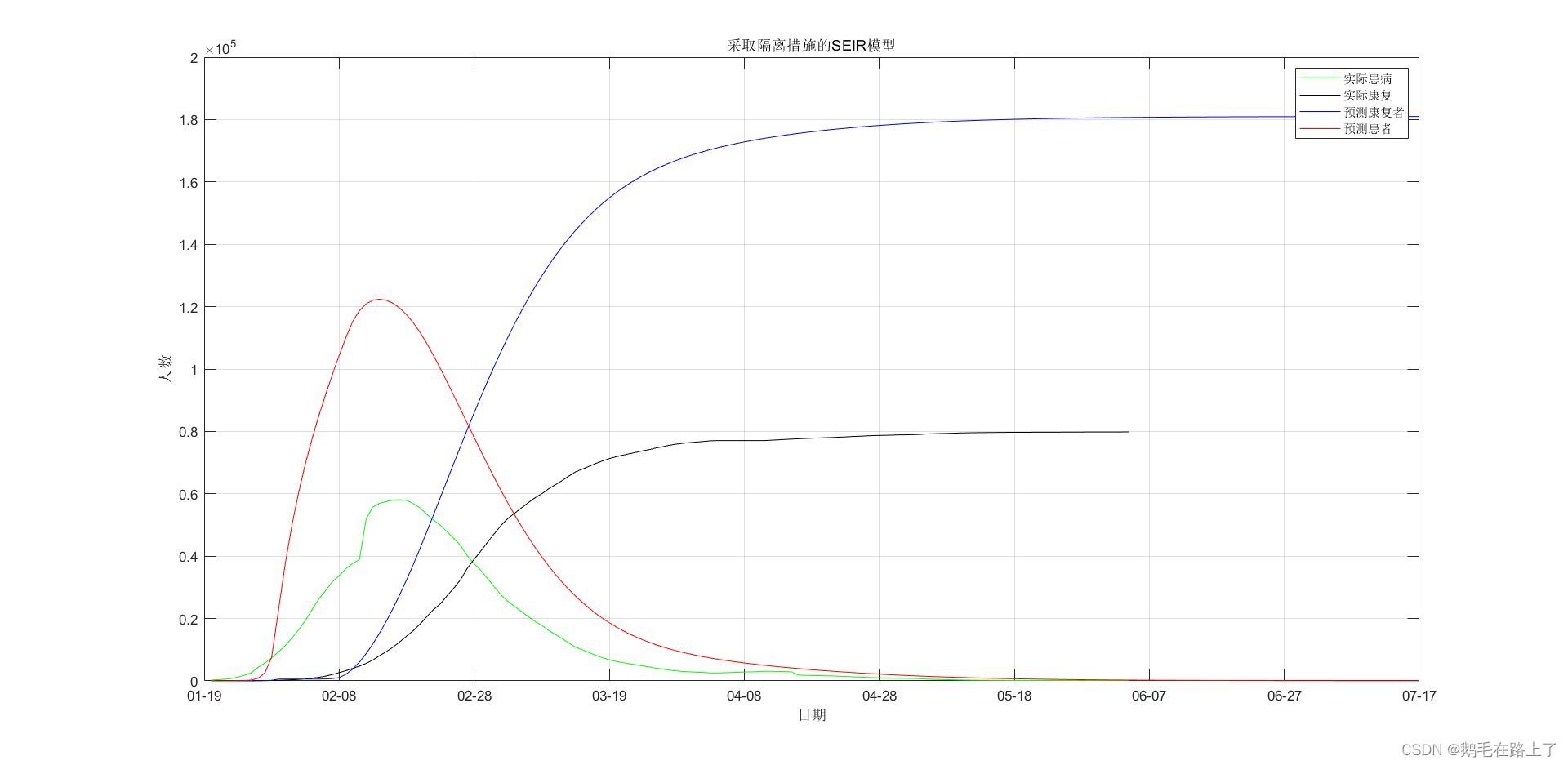
在这里插入图片描述

4. 数据

1. America.mat
1.0 0.0 0.0
1.0 0.0 0.0
2.0 0.0 0.0
2.0 0.0 0.0
3.0 0.0 0.0
5.0 0.0 0.0
5.0 0.0 0.0
5.0 0.0 0.0
5.0 0.0 0.0
5.0 0.0 0.0
5.0 0.0 0.0
5.0 0.0 0.0
5.0 0.0 0.0
12.0 0.0 1.0
12.0 0.0 1.0
12.0 0.0 3.0
12.0 0.0 3.0
12.0 0.0 3.0
13.0 0.0 3.0
13.0 0.0 3.0
14.0 0.0 3.0
15.0 0.0 3.0
15.0 0.0 3.0
15.0 0.0 3.0
15.0 0.0 3.0
15.0 0.0 3.0
15.0 0.0 3.0
15.0 0.0 3.0
15.0 0.0 3.0
34.0 0.0 3.0
34.0 0.0 3.0
34.0 0.0 3.0
53.0 0.0 3.0
57.0 0.0 3.0
60.0 0.0 3.0
60.0 0.0 3.0
64.0 0.0 3.0
69.0 1.0 3.0
89.0 2.0 3.0
106.0 6.0 3.0
126.0 9.0 3.0
161.0 11.0 3.0
233.0 14.0 3.0
338.0 17.0 10.0
445.0 19.0 10.0
572.0 22.0 10.0
717.0 26.0 10.0
1004.0 31.0 10.0
1323.0 38.0 10.0
1832.0 41.0 31.0
2291.0 50.0 41.0
2995.0 60.0 56.0
3782.0 69.0 56.0
5073.0 90.0 56.0
6536.0 116.0 106.0
10525.0 153.0 108.0
14387.0 204.0 121.0
19624.0 260.0 147.0
27111.0 346.0 178.0
39183.0 473.0 178.0
46450.0 586.0 178.0
55231.0 797.0 354.0
69197.0 1046.0 619.0
86012.0 1301.0 753.0
104860.0 1711.0 894.0
124868.0 2190.0 2612.0
143724.0 2566.0 4865.0
165764.0 3170.0 5945.0
189753.0 4081.0 7141.0
216722.0 5137.0 8672.0
255456.0 6532.0 9359.0
288993.0 7793.0 9897.0
312249.0 8503.0 15021.0
337300.0 9627.0 17582.0
374782.0 11697.0 19972.0
400549.0 12907.0 22461.0
431694.0 14789.0 24213.0
469464.0 16711.0 26522.0
503177.0 18777.0 29191.0
529112.0 20549.0 30548.0
556569.0 22063.0 32634.0
587815.0 23599.0 37315.0
614726.0 26126.0 38879.0
650833.0 32707.0 52739.0
679766.0 34705.0 57844.0
709036.0 37104.0 63510.0
740151.0 39193.0 68456.0
765738.0 40670.0 71281.0
792846.0 42491.0 72410.0
825041.0 45340.0 82973.0
849094.0 47684.0 84050.0
886709.0 50243.0 85922.0
929028.0 52371.0 110504.0
960896.0 54265.0 118162.0
987916.0 55425.0 118781.0
1012147.0 56933.0 139419.0
1036417.0 59284.0 143098.0
1065739.0 61715.0 147473.0
1099275.0 63972.0 156089.0
1134059.0 65886.0 161782.0
1163372.0 67535.0 173910.0
1191849.0 68702.0 178671.0
1214023.0 69974.0 188069.0
1239847.0 72381.0 201152.0
1265212.0 74881.0 213126.0
1293907.0 76998.0 217251.0
1324352.0 78701.0 223930.0
1349599.0 80101.0 238081.0
1369943.0 80846.0 256345.0
1388283.0 82018.0 262326.0
1411148.0 83564.0 298643.0
1433375.0 85334.0 310415.0
1460902.0 87025.0 318036.0
1487065.0 88603.0 327774.0
1509444.0 90142.0 339572.0
1531737.0 91061.0 346786.0
1552304.0 92072.0 358918.0
1571328.0 93561.0 361227.0
1595318.0 95021.0 370973.0
1622337.0 96385.0 382936.0
1648283.0 97732.0 403312.0
1668493.0 98706.0 446982.0
1689581.0 99381.0 451745.0
1709388.0 99909.0 465668.0
1728954.0 100686.0 480273.0
1749160.0 102241.0 490256.0
1771631.0 103417.0 499113.0
1796810.0 104626.0 519715.0
1819788.0 105634.0 535371.0
1839679.0 106261.0 599882.0
1861474.0 106990.0 615654.0
1882478.0 108104.0 646414.0
1902031.0 109146.0 688670.0

2. quanguo1.mat
291.0 6.0 25.0
440.0 9.0 25.0
571.0 17.0 25.0
830.0 25.0 34.0
1287.0 41.0 38.0
1975.0 56.0 49.0
2744.0 80.0 51.0
4515.0 106.0 60.0
5974.0 132.0 103.0
7711.0 170.0 124.0
9692.0 213.0 171.0
11791.0 259.0 243.0
14380.0 304.0 328.0
17205.0 361.0 475.0
20438.0 425.0 632.0
24324.0 490.0 892.0
28018.0 563.0 1153.0
31161.0 636.0 1540.0
34594.0 723.0 2052.0
37162.0 812.0 2651.0
40224.0 909.0 3283.0
42708.0 1017.0 3998.0
44730.0 1114.0 4742.0
58839.0 1260.0 5646.0
63932.0 1381.0 6728.0
66575.0 1524.0 8101.0
68584.0 1666.0 9425.0
70637.0 1772.0 10860.0
72528.0 1870.0 12561.0
74276.0 2006.0 14387.0
75101.0 2121.0 16168.0
75993.0 2239.0 18277.0
76392.0 2348.0 20672.0
76846.0 2445.0 22907.0
77262.0 2595.0 24757.0
77779.0 2666.0 27353.0
78190.0 2718.0 29775.0
78630.0 2747.0 32531.0
78959.0 2791.0 36157.0
79389.0 2838.0 39049.0
79968.0 2873.0 41675.0
80174.0 2915.0 44518.0
80302.0 2946.0 47260.0
80422.0 2984.0 49914.0
80565.0 3015.0 52109.0
80710.0 3045.0 53793.0
80813.0 3073.0 55477.0
80859.0 3100.0 57143.0
80904.0 3123.0 58684.0
80924.0 3140.0 59982.0
80955.0 3162.0 61567.0
80992.0 3173.0 62887.0
81003.0 3180.0 64216.0
81021.0 3194.0 65649.0
81048.0 3204.0 67022.0
81077.0 3218.0 67863.0
81116.0 3231.0 68799.0
81151.0 3242.0 69725.0
81235.0 3250.0 70547.0
81300.0 3253.0 71284.0
81416.0 3261.0 71876.0
81498.0 3267.0 72382.0
81600.0 3276.0 72841.0
81747.0 3283.0 73299.0
81846.0 3287.0 73791.0
81960.0 3293.0 74196.0
82078.0 3298.0 74737.0
82213.0 3301.0 75122.0
82341.0 3306.0 75600.0
82447.0 3311.0 75937.0
82545.0 3314.0 76225.0
82631.0 3321.0 76415.0
82724.0 3327.0 76610.0
82802.0 3331.0 76785.0
82875.0 3335.0 76984.0
82930.0 3338.0 77055.0
83005.0 3340.0 77055.0
83071.0 3340.0 77055.0
83157.0 3342.0 77055.0
83249.0 3344.0 77055.0
83305.0 3345.0 77055.0
83369.0 3349.0 77055.0
83482.0 3349.0 77055.0
83597.0 3351.0 77180.0
83696.0 3351.0 77297.0
83745.0 3352.0 77424.0
83797.0 3352.0 77539.0
84149.0 4642.0 77635.0
84180.0 4642.0 77744.0
84201.0 4642.0 77825.0
84237.0 4642.0 77895.0
84250.0 4642.0 77978.0
84287.0 4642.0 78042.0
84302.0 4642.0 78147.0
84311.0 4642.0 78236.0
84324.0 4642.0 78362.0
84338.0 4643.0 78450.0
84341.0 4643.0 78558.0
84347.0 4643.0 78664.0
84367.0 4643.0 78712.0
84369.0 4643.0 78766.0
84373.0 4643.0 78816.0
84387.0 4643.0 78893.0
84391.0 4643.0 78911.0
84393.0 4643.0 78966.0
84403.0 4643.0 79043.0
84404.0 4643.0 79182.0
84407.0 4643.0 79246.0
84414.0 4643.0 79305.0
84416.0 4643.0 79361.0
84416.0 4643.0 79418.0
84435.0 4643.0 79510.0
84450.0 4644.0 79538.0
84451.0 4644.0 79585.0
84461.0 4644.0 79616.0
84465.0 4644.0 79635.0
84471.0 4644.0 79660.0
84478.0 4644.0 79679.0
84487.0 4645.0 79700.0
84494.0 4645.0 79705.0
84503.0 4645.0 79715.0
84506.0 4645.0 79720.0
84516.0 4645.0 79736.0
84522.0 4645.0 79738.0
84522.0 4645.0 79743.0
84525.0 4645.0 79751.0
84536.0 4645.0 79762.0
84543.0 4645.0 79772.0
84545.0 4645.0 79780.0
84547.0 4645.0 79791.0
84561.0 4645.0 79800.0
84569.0 4645.0 79806.0
84572.0 4645.0 79809.0
84593.0 4645.0 79822.0
84603.0 4645.0 79826.0
84602.0 4645.0 79827.0
84608.0 4645.0 79834.0