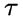整理一下暑假参加的数学建模训练题：）

仅供学习理解传染病模型

源代码仅供参考：MathematicalModeling/COVID-19 at main · AOYLAOTANG/MathematicalModeling · GitHub

一、题目介绍

二、问题分析

2.1问题一：

2.2问题二：

三、问题假设

四、符号说明

五、模型的建立与求解

5.1问题一模型的建立与求解

5.1.1基于改进的SEIR模型建立

5.1.2模型的求解结果与分析

5.2问题二模型的建立与求解

5.2.1针对问题建立改进的SEIR传染病模型

5.2.2估算控制武汉疫情付出的经济代价

六、数据参考来源

一、题目介绍

今年初以来，新型冠状病毒肺炎(以下简称为冠肺炎)疫情在全球暴发，给全世界人民的健康带来了巨大的威胁，也严重影响了我们的经济活动和日常生活。新冠疫情具有以下一些特点：

1.传染源分布广泛，控制传染源难度大：目前认为，传染源主要是新型冠状病毒感染的患者，无症状感染者也可能成为传染源，潜伏期患者可能具有一定传染性。

2.传播途径多样，很难切断所有传播途径：目前认为，新型冠状病毒主要通过呼吸道飞沫传播，也可通过间接接触而传播。

3.人群普遍易感，但目前全人群感染水平不清：新型冠状病毒肺炎是一种人群新发传染病，因人群缺少免疫力，所以普遍易感。

4.新冠病毒是一种新病毒，对它的认识、探索还有一个过程。有效的治疗药物和预防疫苗研发虽已取得进展，但距离使用尚需时间。

我国为应对这次疫情，采取了严格的防控措施，取得了显著的效果。新冠肺炎疫情发生后，基于对新冠肺炎的病原、流行病学、临床特征等特点的认识，经国务院批准，2020年1月20日国家卫健委发布了2020年第1号公告，明确将新型冠状病毒感染的肺炎纳入传染病防治法规定的乙类传染病，并采取甲类传染病的预防、控制措施；我国绝大部分地区相继启动了突发公共卫生事件一级响应。随着疫情被控制,各省市纷纷调低响应级别,5月2日零时,湖北省突发公共卫生应急响应级别由一级调整为二级,自此全国所有省市对新冠肺炎的响应级别都已降为二级及以下。

为了理解国家控制疫情所采取的一系列措施，假设新冠病毒不产生变异,根据已有的信息和数据,研究以下问题,要求得到的任何结论必须来自实际数据以及你们建模分析的结果。

1.如果不积极防控限制出行,经过春节大迁徙,预测3月1号时国内大陆地区疫情最严重的前五个省份或直辖市。在这种情况下预测我国的疫情将会如何发展? 确诊人数和死亡人数可能会达到多少？估算这样的疫情结果(确诊人数和死亡人数)所造成的经济损失。

2.根据武汉市的实际数据分析采取防疫措施后新冠肺炎的传染率和死亡率的变化，同时讨论交通管制防疫措施的经济代价和全国支援武汉医疗资源的力度对这个变化的影响，从而估算我国为控制武汉疫情付出的经济代价。

二、问题分析

2.1问题一：

问题一为考虑武汉不限制人们自由行动，且在春运期间各省人口流动对全国各省疫情的影响。预测出全国疫情最为严重的5个省，计算确诊人数和死亡人数，算这样的疫情结果(确诊人数和死亡人数)所造成的经济损失。因此可以利用传染病模型（SEIR）建立微分方程，并且加入春运人口迁徙对疫情的影响。根据湖北省早期的疫情数据与新型冠状病毒的发病相关信息计算各个必要的参数，利用有限差分的方法将连续传染病模型离散化，计算从发现第一例病情时3月1号这段时间各省疫情情况，得到各省的经济损失。

2.2问题二：

问题二需要利用武汉市的实际数据分析采取防疫措施后新冠肺炎的传染率和死亡率的变化，计算管控防疫措施对疫情的影响，全国支援武汉医疗资源的力度对这个变化的影响如何，从而估算我国为控制武汉疫情付出的经济代价。因此在全国的疫情管控后，每人每天接触他人的数量将大幅减小，并且从武汉到其他地区的潜伏期感染者将近乎于0，将相关参数修改后再次运行模型计算防疫措施下疫情数据变化。全国支援武汉将使得传染病模型中治愈率大幅升高，通过实际数据与计算结果对比，从而估算我国为控制武汉疫情付出的经济代价。

三、问题假设

新冠肺炎传播的过程十分复杂，很多因素都会对新冠肺炎传播的结果产生影响。根据新冠肺炎传播的特点和建模的目的，参照参考文献研究成果，对所建立的模型做了以下假设：

假设政府与个人对疫情不进行防控，人们生活正常运转；
假设每个省份在各个时期的人口数量不变；
假设COVID-19病毒在疫情的各个阶段传染率、恢复率保持不变；
假设每人每天接触的人数保持不变；
假设感染新冠肺炎痊愈之后不会被二次感染；
假设跨省的人员中不存在确诊患者，只存在潜伏期患者与正常人群；
在人口流动过程中，不考虑湖北省以外省份确诊病例传入湖北省的影响；
假设每个地区的客流量在春运期间与非春运期间各自保持不变；
不考虑超级传播者的出现。

四、符号说明

下表中列出了本文所需用到的符号及对该符号的具体说明。

符号	意义
N	该地区人数的人口总数
I(t)	该地区第t天的现存感染人数
E(t)	该地区第t天的潜伏期人数
S(t)	该地区第t天的现存易感人群
R(t)	该地区从疫情开始至第t天累计痊愈人数
D(t)	该地区从疫情开始至第t天累计死亡人数
β	该地区易感人群感染新冠肺炎的概率
γ	患新冠肺炎后的治愈率
d	患新冠肺炎后的病死率
σ	潜伏期患者转化为感染者的比率
k	每人每天平均接触的人数
Inter(t)	第t天迁移到该地区的人数
Out(t)	第t天迁移出该地区的人数
Einter(t)	第t天迁移到该地区潜伏期患者的人数
Eout(t)	第t天迁移出该地区潜伏期患者的人数
M	若不受管控后疫情所造成的经济损失

五、模型的建立与求解

5.1问题一模型的建立与求解

常见的传染病模型有SI、SIR、SIRS、SEIR等模型，由于新冠肺炎具有潜伏期，使用SEIR模型更加贴切、合理。在问题一中，需要考虑在武汉不采取防疫措施的情况下，经过春运的大量人口迁徙，新冠肺炎疫情的发展，所以需要对SIER模型进行改进，加入春运时人口流动的因素。对各个省份建立模型，依据各省常住人口情况以及人口迁徙情况建立微分方程，根据所列的微分方程转换为有限差分方法求解。同时通过计算得到的确诊人数和死亡人数估计疫情所造成的经济损失。

5.1.1基于改进的SEIR模型建立

1、各省总人群的处理

在春运过程中，由于人口流动情况非常复杂，使得各省总人口计算起来非常困难，鉴于各个省份春运人口有流入也有流出，在问题假设中假设各省总人口数量在各个时期保持不变。各个省份在2020年初人口总数情况如下表所示：

省份	人口总数/个	省份	人口总数/个
广东	113460000	黑龙江	37730000
山东	100470000	山西	37180000
河南	96050000	贵州	36000000
四川	83410000	重庆	31020000
江苏	80510000	吉林	27040000
河北	75560000	甘肃	26370000
湖南	68990000	内蒙古	24910000
安徽	63240000	新疆	24870000
湖北	59170000	上海	24240000
浙江	57370000	北京	21540000
广西	49260000	天津	15600000
云南	48300000	海南	9340000
江西	46480000	宁夏	6880000
辽宁	43590000	青海	6030000
福建	39410000	西藏	3350000
陕西	38640000

2、春运人口迁徙处理

春运期间人口迁徙将导致各省疫情发生变化，本文利用百度迁徙以及网上春运资料计算各省春运平均每天迁入迁出的规模。此处迁入地区是湖北则其患病风险高，所以在湖北以外的其他省份迁入迁出需要考虑是否为从湖北迁入。要预测3月1日疫情发展趋势，考虑到春运2月18日春运结束，只有40天时间，在本文中分别计算了春运期间（1月19日-2月18日）与非春运期间（2月19日-3月1日）的湖北迁出的日均客流量，再根据百度迁徙比例计算湖北省每天往其它省份迁徙的人数。

资料[2]为湖北省人民政府所发布的2020年春运部署工作，在这份报告中预测了2020年春运的预计客流量为6450万人，发布公告的日期为2019年12月，尚未发生疫情，该预测为未受干预的预测春运人数Pc。假设湖北省春运客流量输入与输出相等，那么迁出湖北人数为2020年湖北春运客流量的一半。

上图显示了湖北省本省内流动与流入外省的比例，有76.11%是在湖北省内流动，23.89%为流出省外人员，春运天数Dc共有40天，所以春运期间（1月19日-2月18日）湖北省日均流出省外的平均人员Pcout为：

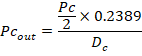
假设不发生重大事件时，每年春运迁徙指数不变；本文利用百度迁徙资料中的2019年湖北迁徙指数分别求取湖北春运期间（1月19日-2月18日）平均迁移指数ζc 与非春运期间（2月19日-3月1日）平均迁移指数ζn，由于迁徙人数与迁徙指数成正比，本文中估算了非春运期间（2月19日-3月1日）湖北省日均流出省外的平均人员Pnout为：

最后利用下图中2019年湖北迁出至其他省份比例λi分别计算出春运期间湖北每日迁出至第i个省份平均人数Pci与非春运期间湖北每日迁出至第i个省份平均人数Pni：

3、湖北省确诊病例数据处理

武汉采取防疫措施是在1月23日，在采取防疫措施之前疾病的传播受到人为干预因素影响较小，所以采用采取防疫措施前的数据来做参数辨识。同时由于无症状感染者的潜伏期大致为7天，所以1月16日-1月23日的感染者数据可以作为未采取防疫措施时感染者变化数据。该时间段内湖北的病例绝大部分来自武汉，可以近似把武汉数据看成湖北省数据，所以从“武汉市新冠肺炎疫情动态”收集得到1月16日-1月23日数据如下表所示：

日期	累计确诊人数
2020.1.16	45
2020.1.17	62
2020.1.18	121
2020.1.19	198
2020.1.20	270
2020.1.21	375
2020.1.22	444
2020.1.23	549

4、基于SEIR的传染率计算模型建立

经典SEIR模型将人群分为易感者（susceptible, S）、感染者（infected, I）、潜伏者（exposed, E）和康复人群（recovered, R )。模型假设人群中所有个体都有被感染的概率，当被感染个体痊愈后，会产生抗体，即康复人群 R不会再被感染。传统SEIR模型公式如下：

利用差分思想对SEIR模型公式进行改变得到：

由于考虑春运客流对各省的影响，所以此处在公式中加入迁入、迁出人数使得公式符合实际情况，差分公式修改为：

其中t单位为天。

5、优化算法传染率计算处理

改进的SEIR模型采用6个差分方程对易感者、潜伏者、感染者、恢复者这四类人群随时间变化的过程进行建模，而模型中的几个重要参数β与γ等的取值将会极大影响预测结果。

因此需要通过湖北武汉早期的疫情数据计算出β与γ，本文中计算β与γ参考钟南山院士团队所研究模型方法进行计算。由于湖北武汉市第一例感染者出现在12月8号，初始感染人数为1，易感人群为N-1，移出人群为0。为了计算出β与γ，在病毒传播的早期有S≈N，将此条件加入到公式（3）中得到：

所以将初始条件It=0=0 ，代入此常微分方程中得到I与t的关系表达式为：

在春运期间平均每人每天可以接触大概15人左右，即r=15，利用Matlab拟合工具箱对表2数据进行拟合，得到符合公式（16）形式的表达式，最终计算得到参数β=0.05249、γ=0.154。

由于疫情的平均潜伏期为7天，在本文中，无症状感染者转化为确诊病例的比率取平均潜伏期的倒数σ=1/7。利用湖北省早期数据可以计算出在不加任何干预下的死亡率为d=0.0675。

6、经济损失求解方法

若疫情不加以管制与约束，每个患者进行治疗需要大量的人力物力，甚至造成人员伤亡的情况，假设每个患者救治需要花费C元，2019年全国人均GPD为W 元，全部确诊患者为I则经济损失M可以使用以下等式进行计算：

5.1.2模型的求解结果与分析

根据上述模型进行分析，利用Matlab软件编程进行求解，模拟了全国31个省（直辖市）在不干预，春运大迁徙的情况下的疫情发展情况，预测3月1号时国内大陆地区疫情最严重的前五个省份或直辖市分别为湖北省、浙江省、广东省、湖南省、河南省。

湖北作为疫情的震中，情况最严重，湖北的疫情情况如下图所示：

预测是从1月23日开始，所以第39天为3月1日，得到了湖北省3月1日的疫情情况为：未感染人数：57072099人，累计感染：947526人，无症状人数：1137077人，现存感染：467257人，治愈人数：416325人，死亡人数：63944人。由我们预测的曲线可以得知，在3月1日时，疫情还在上升期，如果疫情不加控制，疫情会传播越来越快，最终导致大部分人感染。

疫情第二严重的地方为浙江：未感染人数：57334170人，累计感染：90698人，无症状人数：111798人，现存感染：45168人，治愈人数：39409人，死亡人数：6121人，同样，3月1日疫情还在上升期，浙江疫情情况走势图如下图所示：

疫情感染人数预测排行第三的省份为广东省：未感染人数：57334170人，累计感染：90698人，无症状人数：111798人，现存感染：45168人，治愈人数：39409人，死亡人数：6121人，广东疫情情况走势图如下图所示：

疫情感染人数预测排行第四的省份为湖南省：未感染人数：70269033人，累计感染：72735人，无症状人数：92409人，现存感染：36712人，治愈人数：31115人，死亡人数：4908人，湖南疫情情况走势图如下图所示：

疫情感染人数预测排行第五的省份为河南省：未感染人数：96801586人，累计感染：63528人，无症状人数：79600人，现存感染：31853人，治愈人数：27389人，死亡人数：4286人，湖南疫情情况走势图如下图所示：

各省新型冠状病毒疫情数据如下表所示：

省份	累计感染	无症状感染	现存感染	治愈人数	死亡人数
湖北	947526	1137077	467257	416325	63944
浙江	90698	111798	45168	39409	6121
广东	81726	102370	41061	35151	5514
湖南	72745	92638	36744	31094	4907
河南	72735	92409	36712	31115	4908

如果武汉不采取防疫措施，中国大陆到3月1号总共的确诊将会达到1666721人，死亡人数将会达到112457人。通过查阅疫情报告白皮书，平均每个感染者接受治疗所需要的经济代价为2.3万元，治疗消耗的总费用为383.346亿元，而2019年人均GDP为70892元，死亡人数的经济损失为79.723亿元。合计对国家造成的经济损失将会达到约为463.069亿元。

各省3月1日疫情情况分布图如下图所示：

5.2问题二模型的建立与求解

问题二利用了武汉市的实际数据分析采取防疫措施后新冠肺炎的传染率和死亡率的变化，在武汉采取防疫措施实施下，迁入迁出的将不用再考虑，通过实际数据计算，利用SEIR模型反算传染率和死亡率。

全国支援武汉医疗资源的力度将会导致武汉的恢复率升高，减小武汉的死亡人数。因此在武汉采取防疫措施以及全国的疫情管控后，每人每天接触他人的数量将大幅减小，并且从武汉到其他地区的潜伏期感染者将近乎于0，所以要对5.1节中的模型进行修改，并修改相关参数，再次运行模型计算防疫措施下疫情数据变化。全国支援武汉将使得传染病模型中治愈率大幅升高，通过实际数据与计算结果对比，从而估算我国为控制武汉疫情付出的经济代价。

5.2.1针对问题建立改进的SEIR传染病模型

在采取防疫措施后，武汉将变为一个密闭系统，不用再考虑迁入迁出的影响，所以SEIR模型变为：

在采取防疫措施后武汉市的传染率将会降低，所以可以利用优化算法来反算感染率，优化算法即最小化SEIR模型计算的结果与实际结果之间的误差，此时决策变量为β，优化目标函数为：

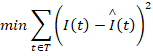
其中，I∧(t)为实际的感染人数随时间变化规律，I(t)为通过改变决策变量β预测得到的感染人数随时间变化规律。通过不断改变β值，使得优化函数得到最小值。

5.2.2估算控制武汉疫情付出的经济代价

本文通过GDP构成的三种产业产值角度分析本次疫情造成的经济损失。

由武汉统计局发布的2019年武汉GDP数据可知，第一、二、三产业GDP总额分别为372.5亿元、6741.3亿元、5926.4亿元，GDP总额为16040.2亿元。由武汉统计局发布公告《2020年上半年武汉市经济运行情况新闻通稿》[8]可知，初步核算上半年武汉市地区生产总值，按可比价格计算，比上年同期下降19.5%。分产业看，第一产业增加值下降14.4%；第二产业增加值下降21.9%；第三产业增加值下降18.2%。整理得到下表：

	第一产业	第二产业	第三产业	合计
2019年GDP	372.5亿元	6741.3亿元	5926.4亿元	16040.2亿元
2020年下降比	14.4%	21.9%	18.2%
疫情损失	53.6亿元	1476.3亿元	1078.6亿元	2608.5亿元