参考文章为：https://www.kesci.com/mw/project/60161bf6ac79f40016b7d7d9

1.SI模型

示意图：

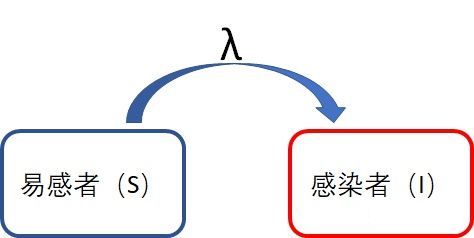
我们假设城市有一千万（N=10的7次方）人，每个患者每天接触感染每天0.8人（lamda=0.8），初始感染人数为45人(i0 = 45/N)，我们来模拟70天(T=70)的情况。

1.1 代码实现

import numpy as np
import matplotlib.pyplot as plt
#population N = 1e7#simuation TimeT = 70
# susceptiable ratio 易感染比例
s = np.zeros([T])
# infective ratio 感染比例
i = np.zeros([T])# 由我们的实验可以知道，lamda是有取值范围的，似乎超过1就不可以了
# concat ratelamda = 0.9# initial infective people i[0] = 45.0 / N
s[0] = 1-i[0]for t in range(T-1):i[t+1] = i[t] + i[t]  * lamda * (1.0 - i[t])s[t+1] = 1 - i[t+1]

1.2 模型的结果

#感染者随着天数的变化曲线
fig, ax = plt.subplots(figsize=(8,4))
ax.plot(i, c='r', lw=2)
ax.plot(s, c='b', lw=2)ax.set_xlabel('Day',fontsize=20)
ax.set_ylabel('Infective Ratio', fontsize=20)
ax.grid(1)
plt.xticks(fontsize=20)plt.yticks(fontsize=20);

由上图可见，大约在25天左右，全部人群都会变成感染者，感染率为1

lamda的现实意义就是该城市的卫生水平，衡量的是消毒，隔离这些措施执行得怎么样。

回到传染病模型，按照SI模型计算的结果，我们全人类都会患病，这好可怕！原因是我们忽略了一个很重要的因素，那就是我们有奋斗在一线的医护人员，我们会被治愈！所以SI模型只适合研究具有高传染风险又不能被治愈的病（比如HIV）。

但是对于其他病，我们是可以靠医疗和自身免疫系统康复的，那么紧接着的一个问题就是，被治愈后还会再被传染上嘛？根据这个问题的回答不同，我们有了两个不同的模型，SIR 和 SIS。现在可以揭晓，SIR的R的含义了，就是移出者（Removed），现实含义就是指被治愈后不会再被感染的人。 而SIS表示治愈后仍然还是易感者。下面我们用python来分别实现这两个模型。

2.SIS （治愈后仍然还是易感者）

为了实现这个模型，我们需要引入新的一个参数，治愈率$\gamma$。好啦，先上我们的新示意图：

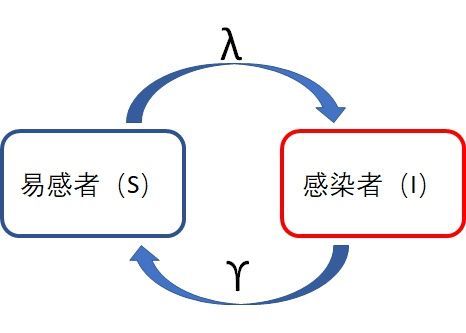
和SI模型做比较，区别就是计算感染者的增加数时要减去被治愈的人数。
所以这时候每天的增加的感染者为：$\lambda \times iN\times s-\gamma \times iN$ ,
增加的感染率为：$\lambda \times i\times s-\gamma i$ 。
模型完成啦，修改python代码：

2.1 代码实现

# susceptiable ratio
s = np.zeros([T])# infective ratioi = np.zeros([T])# concat rate(这个其实是有效的感染率)lamda = 1.0# recover rate(治愈率)gamma = 0.5# initial infective people i[0] = 45.0 / N
s[0] = 1-i[0]for t in range(T-1):i[t+1] = i[t] + i[t] * (1- i[t])* lamda - i[t] * gammas[t+1] = 1 - i[t+1]

2.2模型的结果

 fig, ax = plt.subplots(figsize=(8,4))
ax.plot(i, c='r', lw=2)
ax.plot(s, c='b', lw=2)ax.set_xlabel('Day',fontsize=20)
ax.set_ylabel('Infective Ratio', fontsize=20)
ax.grid(1)
plt.xticks(fontsize=20)
plt.yticks(fontsize=20);

可以看到，达到最大感染率的时间退后10天左右，最后感染和治愈达到动态平衡，人群中有始终有一半的人感染着。所以，SIS模型适合研究具有传染性和反复性的流行病，比如常见流感。同样的，感兴趣的话，改变lamda和gamma的值，观察曲线的变化。和lamda不同的是，gamma的现实意义就是对这种疾病的治疗水平。

3 SIR模型（治愈后直接移除）

加入了移出者，被治愈的病人不会再被传染，先上我们的新示意图：

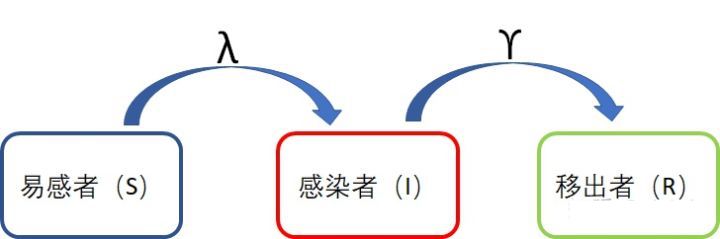
SIR 模型
注意到这里，人群被分成了三类，不再只有I和S，所以相比于之前的模型，我们需要找到新的约束关系。现在我们需要分别计算三种人每天的增加量了：

• 易感者：每天都在被传染，所以一直在减少，减少量为被传染的人数：$\lambda Nis$
• 感染者：增加了被感染的人，减少了治愈的人： $\lambda Nis-\gamma Ni$
• 移出者：增加了治愈的人： $\gamma Ni$

建模完成，修改python代码，并且假设人群普遍易感，新型疾病，初始没有移出者。

$\gamma =0.0821,\lambda =0.2586，初始易感人数为一千万,初始感染10人，那么我们的城市总人数N=1e7+10$

3.2代码实现

# populationN = 1e7 + 10 # simuation Time / Day
T = 170# susceptiable ratios = np.zeros([T])# infective ratioi = np.zeros([T])#remove ratio
r = np.zeros([T])# contact ratelamda = 0.2586# recover rate gamma = 0.0821# initial infective peoplei[0] = 10.0 / Ns[0] = 1e7 / Nfor t in range(T-1):i[t+1] = i[t]+i[t]* lamda * s[t] - gamma*i[t]s[t+1] = s[t] - lamda * i[t]*s[t]r[t+1] =r[t] + gamma * i[t]

3.2绘制图像：

fig, ax = plt.subplots(figsize=(10,6))
ax.plot(s, c='b', lw=2, label='S')
ax.plot(i, c='r', lw=2, label='I')
ax.plot(r, c='g', lw=2, label='R')
ax.set_xlabel('Day',fontsize=20)
ax.set_ylabel('Infective Ratio', fontsize=20)
ax.grid(1)
plt.xticks(fontsize=20)
plt.yticks(fontsize=20)
plt.legend();

感染人数峰值发生在一个月左右，最大感染人数不到人群的20%， 但是最终人群的80%都会得此病（就是最终的移出者的比例）。SIR模型适合研究没有潜伏期的急性传染病，治疗后能够痊愈并具有抗病性。

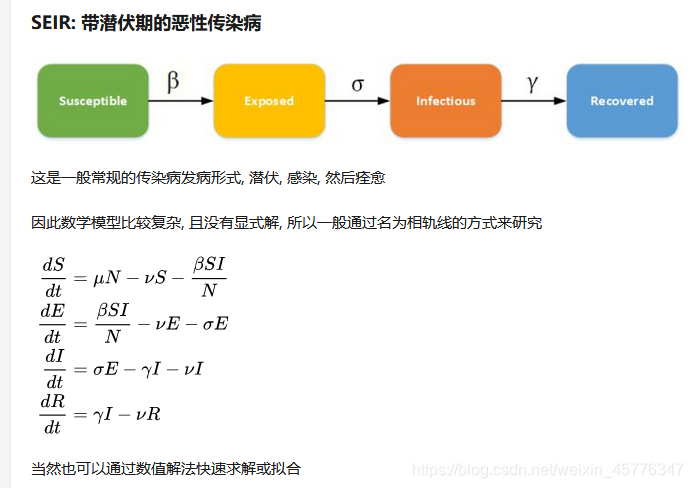
4.SEIR 模型（新增一个人群，叫潜伏者E）

但是，SIR模型和实际情况的出入会比较大，因为忽略了太多因素了，比如说潜伏期，比如说政策调控，药物，出生死亡等等。下面我们可以和前面一样，把潜伏期考虑进去，新增一个人群，叫潜伏者E（exposed）：

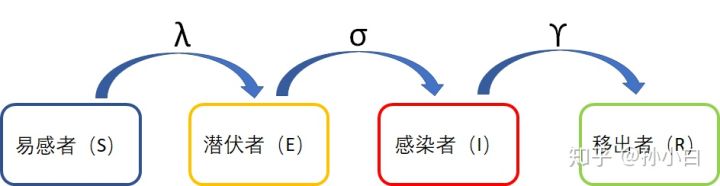
SEIR模型
同样的我们需要计算各人群每天的增加量：

S：每天减少： $\lambda Nis$

E：每天增加传染，减少发病： $\lambda Nis-\sigma Ne$

I：每天增加发病，减少治愈： $\sigma Ne-\gamma Ni$

R：每天增加治愈： $\gamma Ni$

建模完成，修改我们的python程序，这里的 $\sigma$可以理解为潜伏期的倒数。给的4天。新型冠状病毒给目前临床的潜伏期是3-14天。

4.1代码实现

# population
N = 1e7 + 10 + 5
# simuation Time / Day
T = 170
# susceptiable ratio
s = np.zeros([T])
# exposed ratio
e = np.zeros([T])
# infective ratio
i = np.zeros([T])
# remove ratio
r = np.zeros([T])# contact rate
lamda = 0.5
# recover rate
gamma = 0.0821# 潜伏期# exposed periodsigma = 1 / 4# initial infective people
i[0] = 10.0 / N
s[0] = 1e7 / N
e[0] = 40.0 / Nfor t in range(T-1):s[t + 1] = s[t] - lamda * s[t] * i[t]e[t + 1] = e[t] + lamda * s[t] * i[t] - sigma * e[t]i[t + 1] = i[t] + sigma * e[t] - gamma * i[t]r[t + 1] = r[t] + gamma * i[t]

4.2模型的结果

fig, ax = plt.subplots(figsize=(10,6))
ax.plot(s, c='b', lw=2, label='S')
ax.plot(e, c='orange', lw=2, label='E')
ax.plot(i, c='r', lw=2, label='I')
ax.plot(r, c='g', lw=2, label='R')
ax.set_xlabel('Day',fontsize=20)
ax.set_ylabel('Infective Ratio', fontsize=20)
ax.grid(1)
plt.xticks(fontsize=20)
plt.yticks(fontsize=20)
plt.legend();