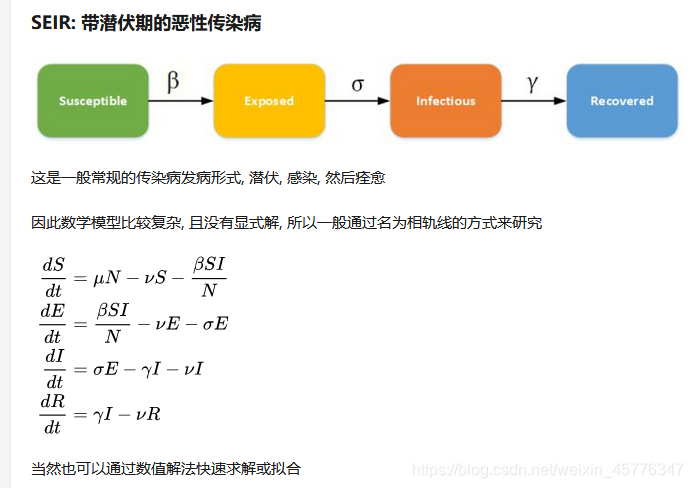
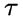目录
- 前言
- 一、模型假设
- 二、符号说明
- 三、SEIRD模型
- 1. 模型求解
- 四、元胞自动机(CA)模型
- 1. 模型求解
- 2. 城市居民减少外出对疫情发展的影响
- 3. 城市间人口流动对疫情发展的影响
- 五 基于防疫政策的修正模型
- 2 “全民戴口罩”
- “早发现,早隔离”
- “全民打疫苗”
- 总结
前言
前段时间参加了校内组织的数学建模比赛,主要是建模预测传染病的发展趋势,下面将模型分享一下:
一、模型假设
将人群分为5类,分别是:易感人群(未感染过病毒的人群),潜伏期人群,感染人群,免疫人群(感染后康复人群)和死亡人群。根据该传染病特征的分析,对问题进行了以下假设:
-
易感人群与潜伏期人群接触不具有感染可能性;
-
易感人群与感染人群接触后有感染可能性;
-
免疫人群具有终身免疫性,只要治愈,就不会再次被感染;
-
死亡人群不具有传染可能性;
-
不考虑在传染病传播期间,人口的迁入迁出以及自然出生和自然死亡对研究区域人口总人数的影响;
-
只考虑人与人之间传播的途径,不考虑环境传播;
-
在疫情的第一天,免疫人群数量和死亡人群数量都为0。
二、符号说明
S S S 易感人群,指未得病,但缺乏免疫力,易在接触感染者后受到感染
E E E 潜伏期人群,指已感染,但无明显感染症状的群体
I I I 感染人群,指染上传染病的人,可以传播给 S S S类成员,将其变为 E E E类或者 I I I类成员
R R R 康复人群,指染上传染病的后康复而具有免疫力的人, R R R类成员不会重新变为 S S S类
D D D 死亡人群,指染上传染病后死亡的人群
α \alpha α 表示易感人群接触感染人群后被转化为潜伏期人群的概率
β \beta β 表示潜伏期人群转化为感染人群的概率
γ \gamma γ 表示感染人群转化为免疫人群的概率
ω \omega ω 表示感染人群转化为死亡人群的概率\
三、SEIRD模型
S E I R SEIR SEIR模型是一种经典的传染病动力学模型,按照传染病的传播顺序,将传染病流行范围内的人分为四类,通过不同的感染率、康复率等实现四类人群的互相转化,以对传染病的传播规模和传播时间进行模拟。但考虑到题目中给出的传染病潜伏期较长的情况,于是对 S E I R SEIR SEIR模型进行改进,增加了死亡人群这一群体。则传染病流行区域内的人群被分为 5 5 5类,分别是:易感人群、潜伏期人群、感染人群、免疫人群和死亡人群,各类人群按照一定的概率进行转化。

S E I R D SEIRD SEIRD模型的动力学过程如图1所示,
其基本思想是:
( 1 ) (1) (1)在不考虑出生、自然死亡、迁入迁出等各种因素的情况下,假设人群总数 N N N不变, t t t时刻各类人群的人数分别记为 S ( t ) , E ( t ) , I ( t ) , R ( t ) S(t),E(t),I(t),R(t) S(t),E(t),I(t),R(t)和 D ( t ) D(t) D(t),则 N = S ( t ) + E ( t ) + I ( t ) + R ( t ) + D ( t ) N=S(t)+E(t)+I(t)+R(t)+D(t) N=S(t)+E(t)+I(t)+R(t)+D(t)。
( 2 ) (2) (2)假设人群中人与人之间的接触是随机的,接触到感染人群(I)的人会以概率 α \alpha α变成潜伏者,则在单位时间 t t t内,接触到感染者变成潜伏者的人数为 α I S N \frac{\alpha IS}{N} NαIS。
( 3 ) (3) (3)潜伏者以概率 β 变 成 感 染 者 , 则 在 单 位 时 间 \beta 变成感染者,则在单位时间 β变成感染者,则在单位时间t 内 , 由 潜 伏 者 变 成 感 染 者 的 人 数 为 β E 内,由潜伏者变成感染者的人数为\beta E 内,由潜伏者变成感染者的人数为βE。
( 4 ) (4) (4)感染者恢复的概率为 γ , 则 在 单 位 时 间 \gamma,则在单位时间 γ,则在单位时间t 内 , 由 感 染 者 变 成 康 复 者 的 人 数 为 γ I 内,由感染者变成康复者的人数为\gamma I 内,由感染者变成康复者的人数为γI。
( 4 ) (4) (4)感染者死亡的概率为 ω \omega ω,则在单位时间 t t t内,因感染传染病而死亡的人数为 ω I \omega I ωI。
综上所述,五类人群的人数随时间的变化情况可用如下的动力学方程表示:

1. 模型求解
为求解微分方程组\ref{eq:1},我们将其转化为迭代形式,具体过程如下。
对
d S d t = − α I S N , \frac{dS}{dt}=-\frac{\alpha I S}{N}, dtdS=−NαIS,
移项得到
d S = − α I S N d t , dS=-\frac{\alpha I S}{N}dt, dS=−NαISdt,
我们在方程两端对 t t t从 n − 1 n-1 n−1到 n n n进行积分
∫ n − 1 n d S = ∫ n − 1 n − α I S N d t . \int_{n-1}^{n}dS=\int_{n-1}^{n}-\frac{\alpha I S}{N}dt. ∫n−1ndS=∫n−1n−NαISdt.
由左矩形公式 ∫ a b g ( x ) ≈ ( b − a ) g ( a ) \int_{a}^{b}g(x)\approx (b-a)g(a) ∫abg(x)≈(b−a)g(a),可得
S ( n ) − S ( n − 1 ) = − [ n − ( n − 1 ) ] α I ( n − 1 ) S ( n − 1 ) N . S(n)-S(n-1)=-[n-(n-1)]\frac{\alpha I(n-1)S(n-1)}{N}. S(n)−S(n−1)=−[n−(n−1)]NαI(n−1)S(n−1).
记 S n = S ( n − 1 ) , I n = I n − 1 S_n=S(n-1),I_n=I_{n-1} Sn=S(n−1),In=In−1,得到
S n − S n − 1 = − α I n − 1 S n − 1 N . S_n-S_{n-1}=-\frac{\alpha I_{n-1}S_{n-1}}{N}. Sn−Sn−1=−NαIn−1Sn−1.
整理得
S n = S n − 1 − α I n − 1 S n − 1 N . S_n=S_{n-1}-\frac{\alpha I_{n-1}S_{n-1}}{N}. Sn=Sn−1−NαIn−1Sn−1.
同理可得
E n = E n − 1 + α I n − 1 S n − 1 N − β E n − 1 , E_n=E_{n-1}+\frac{\alpha I_{n-1} S_{n-1}}{N}-\beta E_{n-1}, En=En−1+NαIn−1Sn−1−βEn−1,
I n = I n − 1 + β E n − 1 − γ I n − 1 − ω I n − 1 , I_n=I_{n-1}+\beta E_{n-1}-\gamma I_{n-1}-\omega I_{n-1}, In=In−1+βEn−1−γIn−1−ωIn−1,
R n = R n − 1 + γ I n − 1 , R_{n}=R_{n-1}+\gamma I_{n-1}, Rn=Rn−1+γIn−1,
D n = D n − 1 + ω I n − 1 . D_n=D_{n-1}+\omega I_{n-1}. Dn=Dn−1+ωIn−1.
由以上式子可以看出,只要给定初始值,就可以求出 S E I R D SEIRD SEIRD模型的数值结果。
将模型的初始值设定为 S 0 = N − E 0 − I 0 − R 0 − D 0 , E 0 = 57 , I 0 = 47 , R 0 = 0 , D 0 = 0 S_0=N-E_0-I_0-R_0-D_0,E_0=57,I_0=47,R_0=0,D_0=0 S0=N−E0−I0−R0−D0,E0=57,I0=47,R0=0,D0=0,城市 A A A的总人口数 N = 100 N=100 N=100万。

图2中展示了 S E I R D SEIRD SEIRD模型结果。图中结果表明:在该地区,传染病在疫情发生半年期间,感染人数会出现爆发式增长,在第 181 181 181天,感染人数达到峰值 636527 636527 636527;此后,感染人群开始逐渐下降,直到传染病消失。最终的免疫人群达到 942356 942356 942356人,最终死亡人数为 57221 57221 57221人。
四、元胞自动机(CA)模型
人员流动时,因该传染病只通过人与人的接触传播,因此每个人的状态只与周围人员的状态相关。
假设某个体所处位置为 ( i , j ) (i,j) (i,j),如果个体的身体是健康的,但是周围存在感染者,则个体会以概率 α \alpha α变成潜伏者;
如果个体是潜伏者,会以概率 β \beta β变成感染者;如果个体是感染者,会以概率 γ \gamma γ变成康复者或以概率 ω \omega ω死亡。
于是通过初始化城市中的人口位置,并放置传染源,可模拟出该传染病的传染过程。
在城市中,根据人口流动程度,可将元胞划分为静态元胞和动态元胞。静态元胞处的值始终为-1,并保持不变,表示此处人口流量为0;动态元胞的值在0到4之间转化,表示由于人口流动导致的病毒传播。在目标区域中,用此区域中动态元胞和静态元胞数目之比表示该区域的人口流动密度,动态元胞越多,表示此处人口流动密度越大;反之,表示人口流动密度越小。将城市内的人口分布情况初始化,然后城市内每个人在自己所处位置附近流动。如图3所示,用不同颜色表示个体所处状态,白色表示静态元胞,可认为该个体为居家隔离状态;绿色表示处于流动状态的易感者;黄色表示处于流动状态的潜伏者;红色表示处于流动状态的感染者;蓝色表示处于流动状态的免疫者;黑色表示死亡状态。

假设人口流动遵循以下规则:
( 1 ) (1) (1)当且仅当个体周围位置为有人状态时,人口流动才有可能发生;
( 2 ) (2) (2)人口流动仅在个体所处位置附近发生;
( 3 ) (3) (3)个体状态的改变是个随机过程,可随机确定,由其邻居的状态随机决定。
假设该地区一共有 n n n个城市,则 S k , E k , I k , R k , D k S_k,E_k,I_k,R_k,D_k Sk,Ek,Ik,Rk,Dk分别表示第 k k k个城市中的易感人群、潜伏期人群、感染人群、康复人群和死亡人群。
每个城市内的各类人群按照一定的概率进行转化,此时的 S E I R D SEIRD SEIRD模型的基本思想为:
( 1 ) (1) (1)在不考虑出生、自然死亡、迁入迁出等各种因素的情况下,假设 n n n个城市的人群总数 N N N不变, t t t时刻第 k k k个城市中各类人群的人数分别记为 S k ( t ) , E k ( t ) , I k ( t ) , R k ( t ) S_k(t),E_k(t),I_k(t),R_k(t) Sk(t),Ek(t),Ik(t),Rk(t)和 D k ( t ) D_k(t) Dk(t),则 N = ∑ k = 1 n [ S k ( t ) + E k ( t ) + I k ( t ) + R k ( t ) + D k ( t ) ] N=\sum_{k=1}^{n}[S_k(t)+E_k(t)+I_k(t)+R_k(t)+D_k(t)] N=∑k=1n[Sk(t)+Ek(t)+Ik(t)+Rk(t)+Dk(t)]。
( 2 ) (2) (2)假设人群中人与人之间的接触是随机的,接触到感染者的人会以概率 α 变 成 潜 伏 者 , 则 在 单 位 时 间 \alpha 变成潜伏者,则在单位时间 α变成潜伏者,则在单位时间t 内 , 第 内,第 内,第k 个 城 市 中 接 触 到 感 染 者 变 成 潜 伏 者 的 人 数 为 个城市中接触到感染者变成潜伏者的人数为 个城市中接触到感染者变成潜伏者的人数为 α I k S k N \frac{\alpha I_kS_k}{N} NαIkSk。
( 3 ) (3) (3)潜伏者以概率 β 变 成 感 染 者 , 则 在 单 位 时 间 \beta 变成感染者,则在单位时间 β变成感染者,则在单位时间t 内 , 第 内,第 内,第k 个 城 市 中 由 潜 伏 者 变 成 感 染 者 的 人 数 为 个城市中由潜伏者变成感染者的人数为 个城市中由潜伏者变成感染者的人数为 β E k \beta E_k βEk。
( 4 ) (4) (4)感染者恢复的概率为 γ \gamma γ,则在单位时间 t t t内,第 k k k个城市中由感染者变成康复者的人数为 γ I k \gamma I_k γIk。
( 4 ) (4) (4)感染者死亡的概率为 ω \omega ω,则在单位时间 t t t内,第 k k k个城市中因感染传染病而死亡的人数为 ω I k \omega I_k ωIk。
( 5 ) (5) (5)因人口流动导致的易感者、潜伏者、感染者和康复者的人口数量差为 Δ n S , Δ n E , Δ n I , Δ n R \Delta n_S,\Delta n_E,\Delta n_I,\Delta n_R ΔnS,ΔnE,ΔnI,ΔnR。
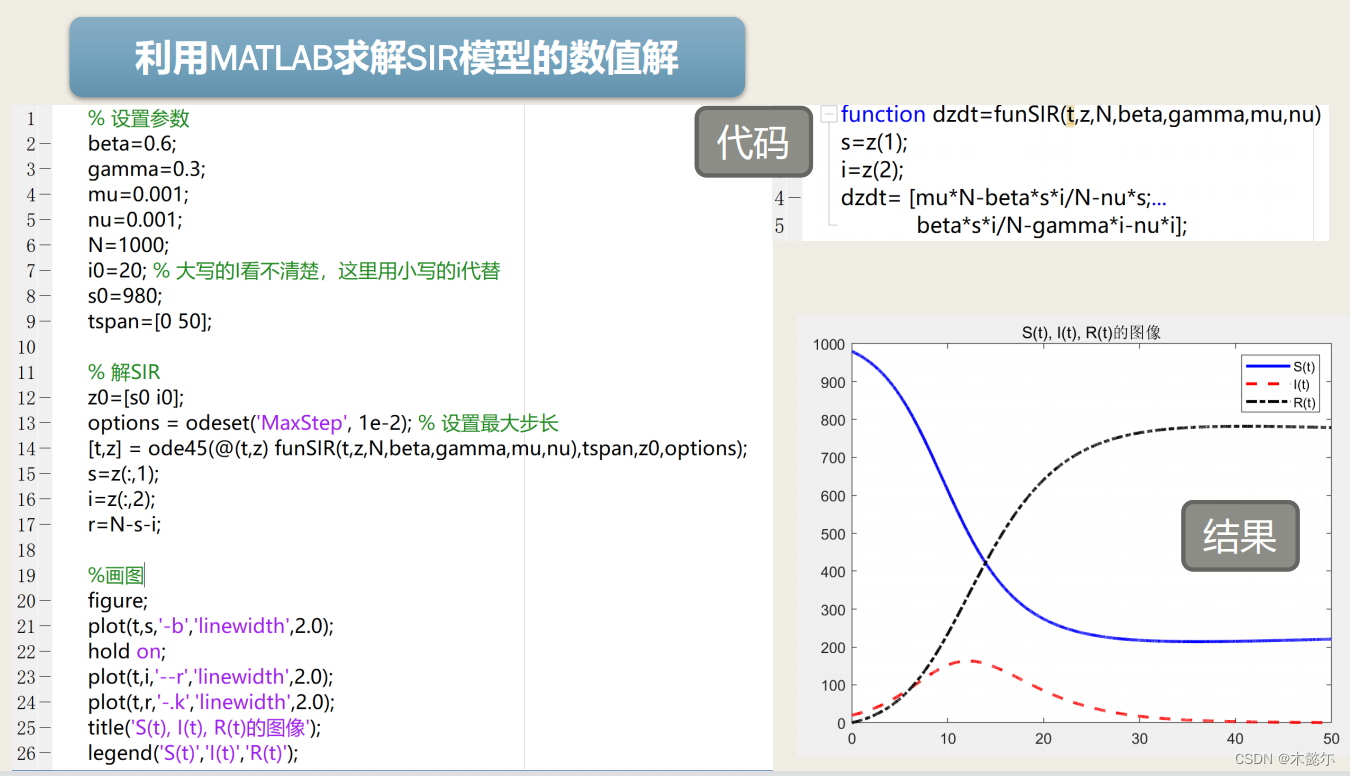
此时,五类人群的人数随时间的变化情况可用如下的动力学方程表示:
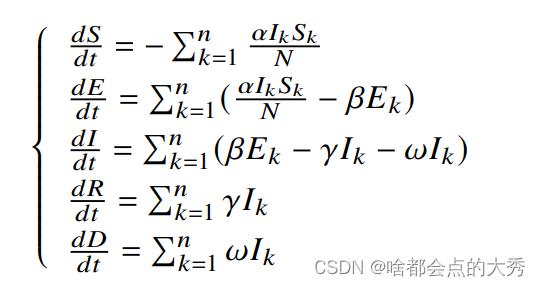
1. 模型求解
使用二维元胞自动机方法,假设种群总数目为 N N N × \times × N N N的元胞空间,每一个元胞代表一个种群个体,元胞的领域采用半径为 1 1 1的 V o n N e u m a n n Von Neumann VonNeumann邻居,每一个元胞在下一时刻的状态取决于自身及其领域中的元胞在当前时刻的状态,个体的状态逐步影响到周围邻居,从而导致整个元胞空间的变化。
采用 s ( i , j , t , k ) s(i,j,t,k) s(i,j,t,k)表示城市 k k k、坐标为 ( i , j ) (i,j) (i,j)的元胞在 t t t时刻的状态。
每个元胞有 6 6 6种状态:
( 1 ) (1) (1)空置状态,此状态下元胞不可被个体占据,始终保持此状态不变;
( 2 ) (2) (2)健康状态,在某个元胞的领域内如果存在感染者,那么该元胞会以概率 α \alpha α成为潜伏者;
( 3 ) (3) (3)潜伏者,在某个元胞的领域内如果存在感染者,那么该元胞会以概率 β \beta β成为感染者;
( 4 ) (4) (4)感染者,感染者以概率 γ \gamma γ获得免疫,成为康复者;以概率 ω \omega ω死亡,成为死亡者;
( 5 ) (5) (5)康复者,获得绝对免疫的人,将不会再受到该类传染病的传染;
( 6 ) (6) (6)死亡者,感染者因病死亡,成为死亡者。
2. 城市居民减少外出对疫情发展的影响
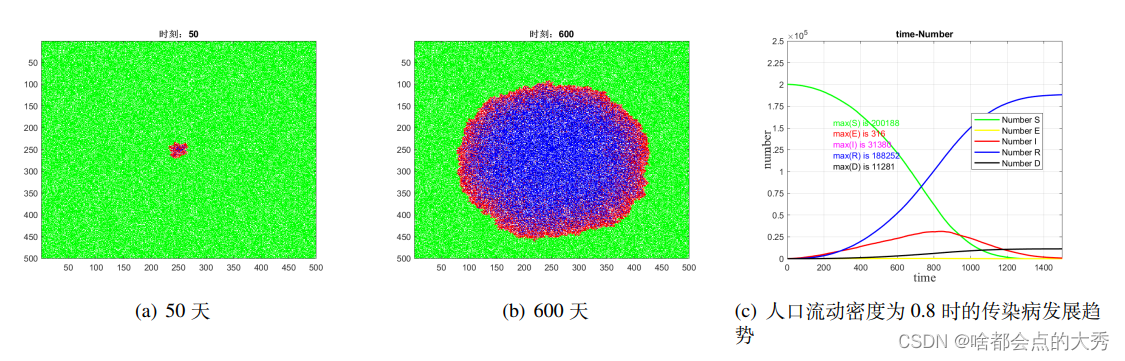
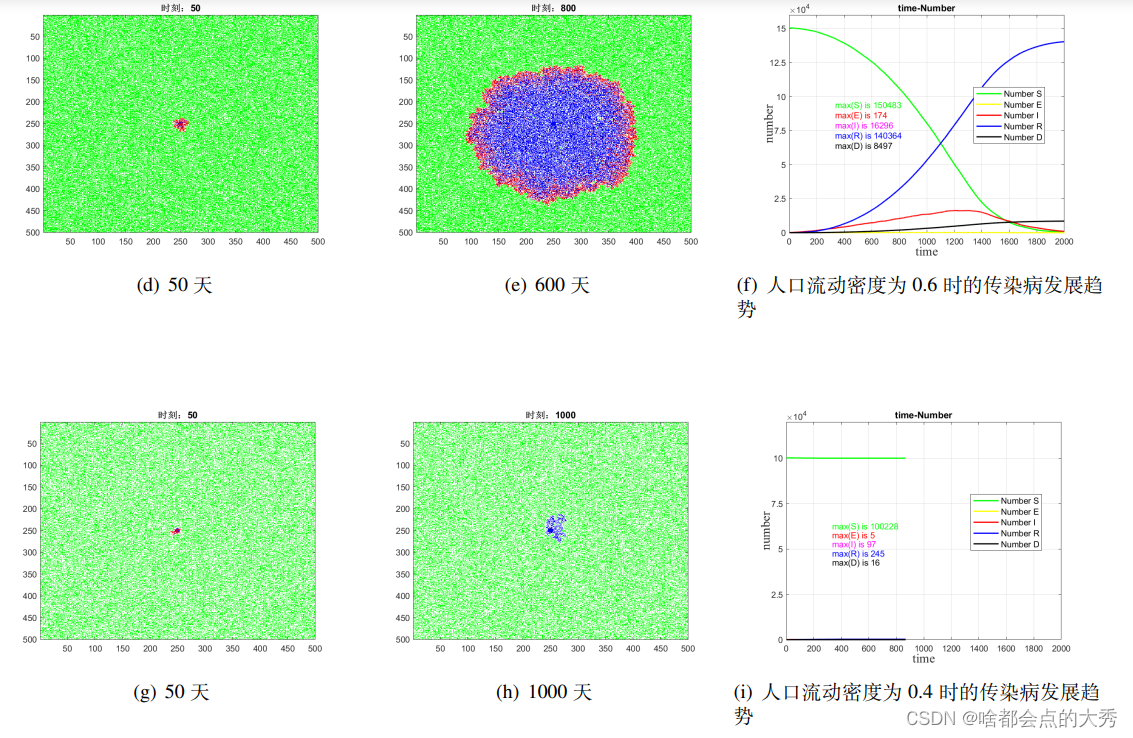
当居民和城市有较强的防疫意识时,会进行居家隔离,于是城市中的人口流动密度(动态元胞减少)降低。我们研究并比较了三组不同人口流动密度时的疫情发展规律。如图4所示,三组图分别表示人口流动密度为0.8,0.6和0.4时的传染病传播动态变化。
流动密度较低时,相对应的图中的白色元胞越多,说明居家隔离措施执行严格,市民大多数处于静态状态。模拟结果显示,在人口密度依次取0.8、0.6以及0.4时,单日最大感染人数分别为31380、16296和97,最终死亡人数分别为11281、8497和16,两者都大大降低。因此,市民居家隔离,减少外出能降低疫情传播,是全民参与抗疫的主要方式。
3. 城市间人口流动对疫情发展的影响
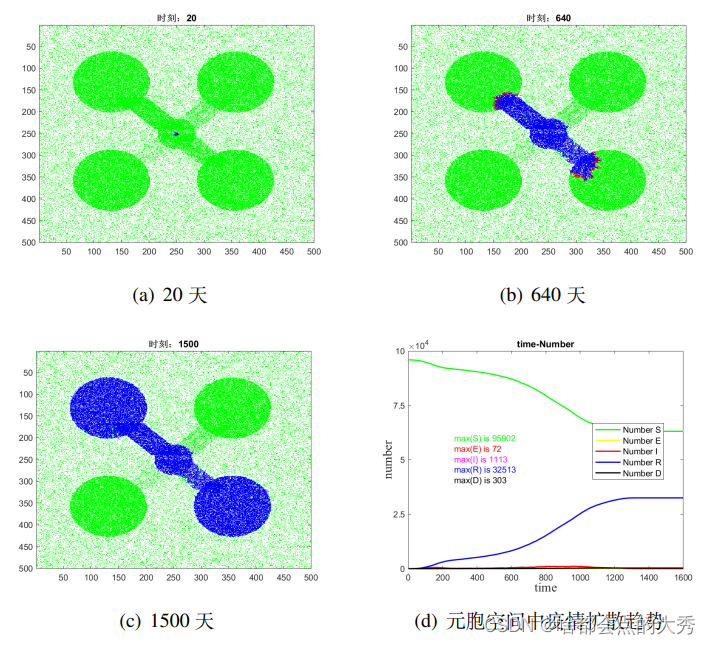
为了研究城市间人口流动对疫情发展的影响,我们在人群总人数为 N = 25 N=25 N=25万的元胞空间中建立了5个城市,研究不同城市间的人口流量密度与病毒扩散的关系。如图5所示,我们假设病毒在中心城市爆发,我们分别设置城市间通道的人口流量密度为0.8,0.6,0.4,0.2,发现当人口流量密度越大,即两个城市间人口流动越大时,感染人数越多;当人口流动密度为0.6和0.8(大于0.6)时,病毒的扩散不受影响,仍然会在城市间传播;当人口流动密度为0.2和0.4(小于0.4)时,能有效抑制病毒在城市中的扩散。由此,我们发现,降低城市间的人口流动,实行城市封控政策对抗击疫情具有重要作用。
五 基于防疫政策的修正模型
自2019年以来,新冠突袭无疑成为人类史上的一大灾难,所幸我国政策制定者采取了有效的政策,举国抗疫,遏制了疫情的发展,保护了人民的生命财产安全。这些政策和手段也为我们建立模型提供了参考。
(1)当病毒在人群之间传播时,感染者和易感者戴口罩都能有效遏制病毒的传播;
(2)当病毒在大范围人群中爆发时,所有人居家隔离,宅家抗疫是对疫情传播的有效打击;
(3)当病毒在大范围人群中爆发时,对该范围地区及时封控,能阻断病毒向其他地区扩散;
(4)实行“早发现,早隔离”,增大检疫次数,并将潜伏者和感染者集中治疗(建立方舱医院)能有效控制疫情;
(4)人们及时注射病毒疫苗,能增加人群的整体免疫能力。
现实生活中,人们会因疫情的变化而做出相对应的政策调整,以此来实现病毒的“动态清零”。通过上面的分析,考虑人们带口罩,实行“早发现,早隔离”政策以及全民打疫苗时的情况。
由所建立的 S E I R D SEIRD SEIRD模型可知,如果能通过政府制定的政策影响到模型中的系数 α , β , γ , ω \alpha,\beta,\gamma,\omega α,β,γ,ω,则可间接达到影响到传染病传播的目的。
假设政府实施如下政策:
(1)所有人口非必要不外出,即使外出在公共场所也必须佩戴口罩,并加紧研发传染病疫苗等,则所有人被感染的概率将会降低 λ 1 \lambda_1 λ1 ;
(2)将与感染者密接后的潜伏者全部集中隔离并进行治疗,降低其转化为感染者的概率,使潜伏者以概率 λ 2 \lambda_2 λ2直接康复;
(3)将所有感染者集中隔离管理与治疗,使其康复几率提升 λ 3 \lambda_3 λ3,死亡几率降低 λ 4 \lambda_4 λ4。
基于如上假设,得到修正的 S E I R D SEIRD SEIRD模型如下:
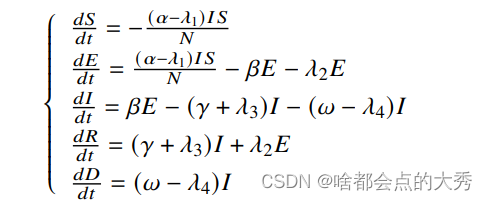
2 “全民戴口罩”
研究人员发现,感染者戴口罩和易感者不带口罩与感染者不戴口罩和易感者戴口罩导致的病毒感染概率并不相同。我们只研究全民(5类人群)戴口罩时的病毒传播情况。戴口罩能降低感染人群将病毒传染给易感人群的概率,为此,在SEIRD模型的基础上,减小 α \alpha α的值。取 α = 0.05 , β = 0.5263 , γ = 0.00861538 , ω = 0.000522308 \alpha =0.05,\beta =0.5263,\gamma=0.00861538,\omega=0.000522308 α=0.05,β=0.5263,γ=0.00861538,ω=0.000522308,如图6为全民戴口罩时疫情的发展趋势,结果表明,疫情在291天时达到最大感染人数,当天感染人数为501135,最终的免疫人群数量为937702人,死亡人数为56938人。戴口罩能推迟疫情爆发的时间点,较小程度的降低感染人数和死亡人数,不能从根本上阻断病毒的传播。

“早发现,早隔离”
“早发现,早隔离”是控制感染源的一种抗疫措施,通过病毒检疫发现感染者并将其集中隔离与治疗。此措施能降低 α \alpha α、 β \beta β和 ω \omega ω,增大 γ \gamma γ。取 α = 0.04 , β = 0.4 , γ = 0.02 , ω = 0.0002 \alpha =0.04,\beta =0.4,\gamma=0.02,\omega=0.0002 α=0.04,β=0.4,γ=0.02,ω=0.0002,如图7为采取该措施时疫情的发展趋势。结果表明,感染人数在503天时达到峰值,当天有143433人感染,最终有7801人死亡。与SEIRD结果相比,该措施有显著抗疫效果,其不仅能大大降低感染人数和死亡人数,也能推迟疫情爆发期,使人们在疫情爆发前做好防疫措施。

我们也研究了在疫情爆发前加强防疫措施对疫情发展的影响,上述疫情在503天时感染人数达到峰值,为了降低该数值,在400天时严格执行“早发现,早隔离”的防疫措施。如图8为在400天时加强抗疫后的疫情趋势,结果表明,感染人数在445天时感染人数达到峰值,当天有83245人感染,最终有3825人死亡。与在疫情爆发前不加强防疫相比,感染人数和死亡人数大大降低。因此,在疫情爆发前严格落实防疫政策,加强防疫措施是防疫重要举措。

“全民打疫苗”
城市全体居民注射疫苗是抗击病毒的最有效措施,也是根本措施。在SEIRD模型中,假设疫苗只对易感人群有效,当易感人群注射疫苗后直接转化为免疫人群,于是SEIRD模型动力学微分方程变为:

在该模型中,我们取与SEIRD相同的参数来研究全民注射疫苗后的疫情发展趋势,其中, η \eta η=0.01,即每天有0.01 × \times ×S 数量的易感者注射疫苗并转化为免疫者。如图9为注射疫苗后的疫情发展趋势,结果表明,当疫情经过500天时基本结束,单日最大感染人数为10698人,最终死亡人数为1526人。与SEIRD结果相比,注射疫苗是抗击疫情的绝对途径,能将感染人数与死亡人数降至最低,是控制疫情的最有效措施。

总结
国家带领全国民众成功狙击病毒的政策和举措为我们建立模型提供了参考。带口罩,居家隔离,城市封控,方舱医院 (“早发现,早隔离”), 疫苗等防疫措施和政策共同实现了病毒的“动态清零”。戴口罩不是消灭病毒的根本方法,但其能大大推迟疫情爆发的时间,实行“早发现,早隔离”是抗击病毒传播的有效方式,“全民打疫苗”是结束疫情的最有效方式并且在单日感染人数达到峰值前加强抗疫措施能改变疫情走势,降低感染人数和死亡人数。
本文所涉及到的matlab CA 代码已经在GITHUB开源,链接如下:
https://github.com/Bigfoots/Epidemic-model-based-on-Cell-automatic
求解微分方程的代码网上有许多,我用的PYTHON求解微分方程。