【Python数学建模】SEIR传染病模型模型延伸-SEIDR模型（一），加入疫苗接种、政府管控、病毒变异等因素的影响

article/2025/9/25 11:45:17

一. SEIR传染病模型

二. SEIR模型的延伸——SEIDR模型

三. 模型延伸——影响因素1：疫苗接种

四. 模型延伸——影响因素2：政府管控

五. 模型延伸——影响因素3：病毒变异

写在前面：

需要源代码的小伙伴可以移步到我的GitHub仓库https://github.com/moyuweiqing/SEIR-Model-extension 中进行获取，如果觉得我的文章或代码帮助到你的话，不妨在文章或GitHub代码中给我点个赞，谢谢大家！

一. SEIR传染病模型

SEIR传染病模型是一个在数据建模中常见的基础模型，其中分为以下四类人群：

S (Susceptible)，易感者，指缺乏免疫能力健康人，与感染者接触后容易受到感染；

E (Exposed)，暴露者/潜伏者 ，指接触过感染者，在还未发病或发生症状的人，可用于存在潜伏期的传染病；暴露者可以有传染性，具体取决于模型和传染病本身情况；

I (Infectious)，患病者，指有传染性的病人，可以传播给 S，将其变为 E 或 I ；

R (Recovered)，康复者，指病愈后具有免疫力的人；康复者可以终身免疫，或者是受到二次感染。

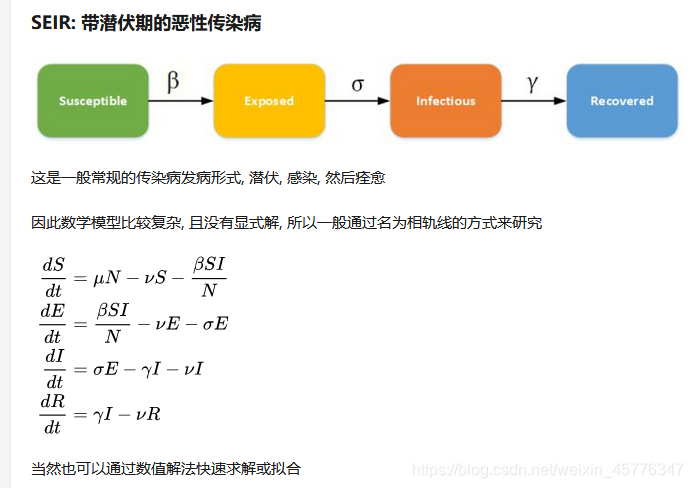
图1 SEIR模型人群转化图

其基本公式如下：

$dS/dt = -r\beta (I+E) S / N$

$dE/dt = r\beta (I + E)S / N - \alpha E$

$dI/dt = \alpha E - \gamma I$

$dR/dt = \gamma I$

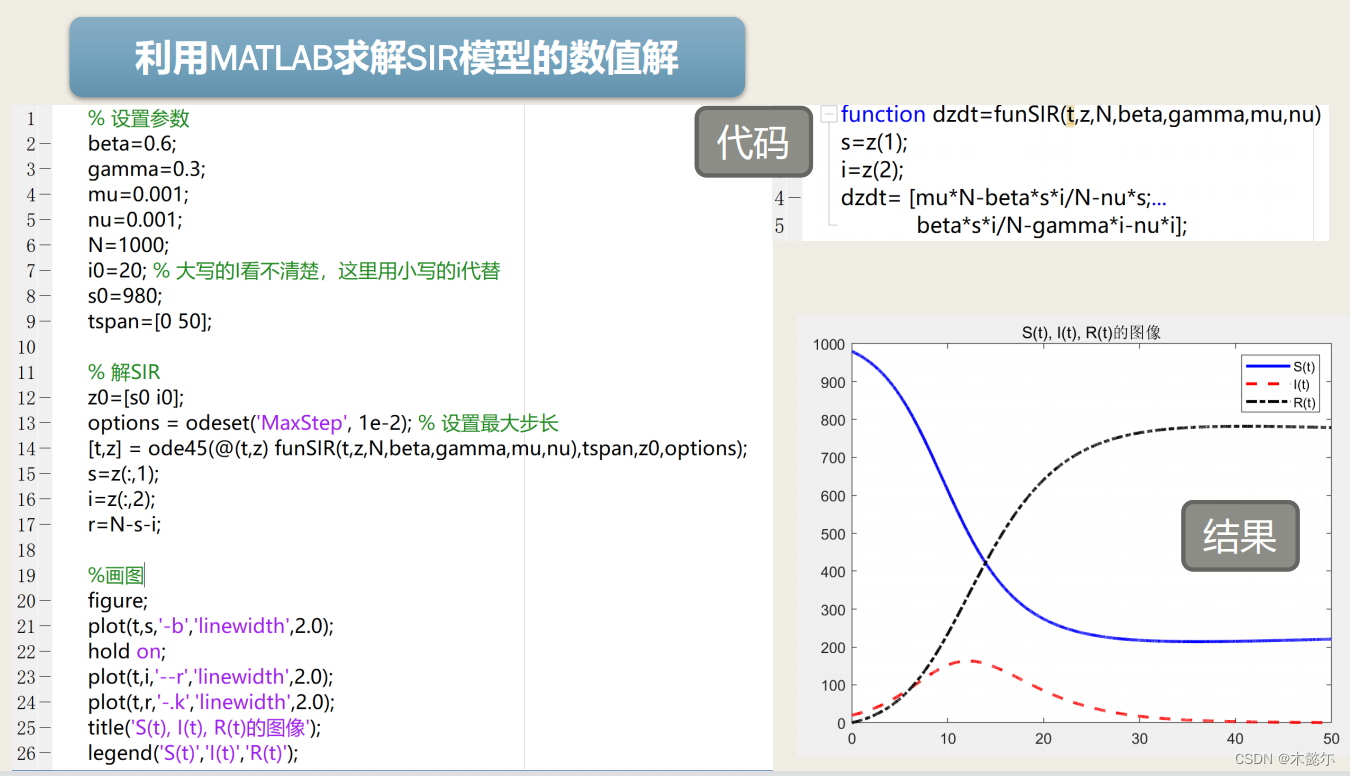
此模型无解析解，给定指定的参数可求数值解。

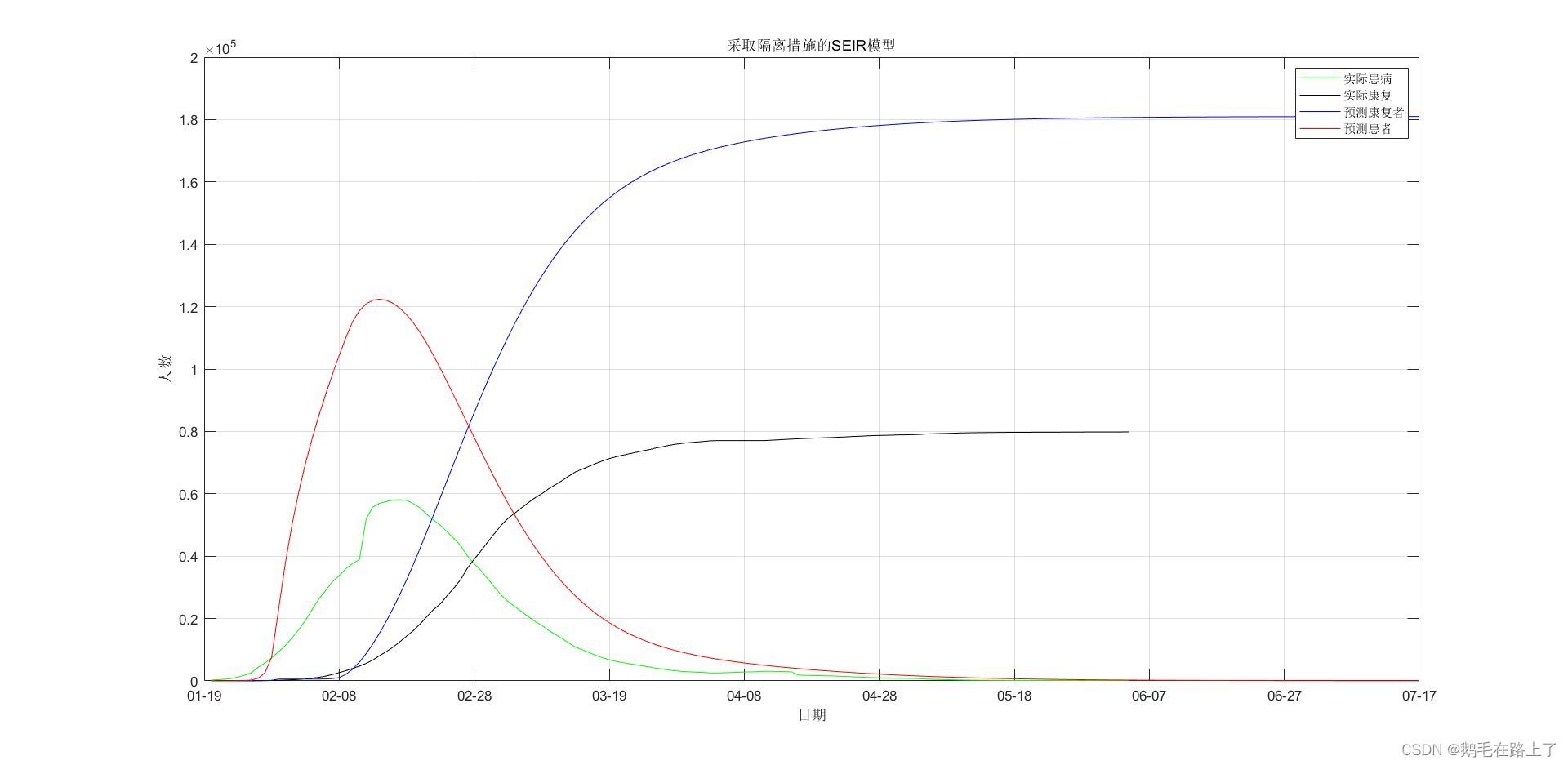
图2 SEIR模型

二. SEIR模型的延伸——SEIDR模型

在这里，假定患病者(Infectious)在患病期间有概率康复或死亡，设定死亡率为 $\delta$ ；则在患病期间，患者可以转化为康复者(Recovered)和死亡者(Dead)，则延伸为SEIDR模型，其微分公式如下：

$dS/dt = -r\beta (I+E) S / N$

$dE/dt = r\beta (I + E)S / N - \alpha E$

$dI/dt = \alpha E - \gamma I - \delta I$

$dD/dt = \delta I$

$dR/dt = \gamma I$

此时，日死亡率为 $\delta$ ，日治愈率为 $\gamma$ ，该传染病的致死率为 $\delta / \left (\delta +\gamma \right )$ 。例如，日死亡率 $\delta$ =0.02，日治愈率为 $\gamma$ =0.10，该传染病的致死率为 $\delta / \left (\delta +\gamma \right )$ = 0.02 / ( 0.02 + 0.10 ) * 100% = 16.7%

python的模型微分代码如下：

ds_dt = - lamda * beta * s * (i + e) / n
de_dt = lamda * beta * s * (i + e) / n - alpha * e
di_dt = alpha * e - gamma * i - delta * i
dd_dt = delta * i
dr_dt = gamma * i

此时，模型的效果图如下：

图3 SEIDR模型

三. 模型延伸——影响因素1：疫苗接种

引入疫苗(vaccine)的接种影响因素，接种疫苗可以直接反映在SEIDR中的感染率 $\beta$ 、死亡率 $\delta$ 、康复率 $\gamma$ ，影响传染病的致死率 $\delta / \left (\delta +\gamma \right )$ 数值情况。具体的影响可以基本分为以下四种情况作进一步讨论：

一剂疫苗，在传染病发生时期即存在疫苗，在传染病爆发的同时开始接种疫苗。
一剂疫苗，传染病发生时并无疫苗，疫苗相对于传染病传播具有延迟性，在传染病开始爆发T日后开始接种疫苗。
二剂疫苗，在传染病发生时期即存在疫苗，在传染病爆发的同时开始接种第一剂疫苗；在两针疫苗的间隔期后开始接种第二剂疫苗。
二剂疫苗，传染病发生时并无疫苗，疫苗相对于传染病传播具有延迟性，在传染病开始爆发T日后开始接种第一剂疫苗；在两针疫苗的间隔期后开始接种第二剂疫苗。

引入该变量后，模型的基本微分公式如下：

$dS/dt = \sum -r\beta _{i} \left ( I+E \right )/N+\sum \nu _{j} S_{i},\: \: \: \: i\epsilon (0,1,2), j\epsilon (1,2)$

$dE/dt = \sum r\beta _{i} \left ( I+E \right )/N+\sum \alpha E_{i},\: \: \: \: i\epsilon (0,1,2)$

$dI/dt = \sum \left ( \alpha E_{i} - \gamma_{i} I_{i} -\delta_{i} I_{i} \right),\: \: \: \: \: i\epsilon \left ( 0, 1, 2 \right )$

$dD/dt = \sum \delta _{i}I_{i}, \: \: \: \: \: i\epsilon \left ( 0, 1,2 \right )$

$dR/dt = \sum \gamma _{i}I_{i},\: \: \: \: \: i\epsilon \left ( 0, 1, 2 \right )$

其中， $i\epsilon (0,1,2)$ 是对应的是未接种疫苗、接种一剂疫苗和接种两剂疫苗的情况， $S_{i}$ 、 $E_{i}$ 、 $I_{i}$ 分别是不同疫苗接种情况的易感人群、潜伏者和感染者， $\beta _{i}$ 、 $\gamma_{i}$ 、 $\delta_{i}$ 分别对应不同疫苗接种情况下各个人群的患病率、康复率、死亡率。 $\nu _{j}, j\epsilon \left ( 1,2 \right )$ 表示一剂疫苗的日接种率和二剂疫苗的日接种率。

具体的一个样例如下：

ds0_dt = - lamda * beta0 * s0 * i_e / n - v1 * s0
ds1_dt = - lamda * beta1 * s1 * i_e / n + v1 * s0 - v2 * s1
ds2_dt = - lamda * beta2 * s2 * i_e / n + v2 * s1
de0_dt = lamda * beta0 * s0 * i_e / n - alpha * e0
de1_dt = lamda * beta1 * s1 * i_e / n - alpha * e1
de2_dt = lamda * beta2 * s2 * i_e / n - alpha * e2
di0_dt = alpha * e0 - gamma0 * i0 - delta0 * i0
di1_dt = alpha * e1 - gamma1 * i1 - delta1 * i1
di2_dt = alpha * e2 - gamma2 * i2 - delta2 * i2
dd0_dt = delta0 * i0
dd1_dt = delta1 * i1
dd2_dt = delta2 * i2
dr_dt = gamma0 * i0 + gamma1 * i1 + gamma2 * i2

此时，模型的效果图如下：

图4 SEIDR_V2t模型

四. 模型延伸——影响因素2：政府管控

在传染病影响情况较为严重的情况下，政府会进行管控，政府通过不同的手段和措施进行管控，其不同的手段和措施会影响某一些参数。例如，如果政府通过采取措施限制人员接触，其在模型中会直接影响到单位时间内受感染者接触的易感人群数量 $r$ ，在政府采取限制人员接触的措施后， $r$ 的数值会降低。

具体案例如下：

if t < 30:         # 从第30天开始限制人员接触r = 5
else:r = 2

此时，模型的效果图如下：

图5 SEIDR_G模型

五. 模型延伸——影响因素3：病毒变异

考虑病毒变异的影响，在传染病的传播过程中，病毒会发生变异，使得其传染性和致死率会发生变化。例如在本次Covid-19的疫情影响中，从最开始的毒株，后面变异到传染性更强的德尔塔毒株，以及后面的奥密克戎毒株，其传染性逐渐变强，而其致死率反而逐渐降低。因此，在时间维度上引入病毒变异的情况，其在模型中会直接影响到感染率 $\beta$ 和致死率 $\delta$ 。

具体案例如下：

if t >= 30 and t <= 60:                 # 从第30天开始病毒发生变异beta = beta * 1.2                   # 传染性增强delta = delta * 0.8                 # 致死性降低
elif t > 60:                            # 第二次变异beta = beta * 1.5                   # 传染性进一步增强delta = delta * 0.5                 # 致死性进一步降低

此时，模型的效果图如下：