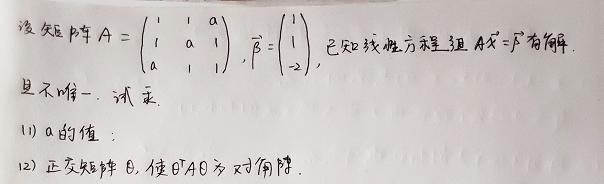参考文献
前言
在上一篇博客SQL Kerberos的原理及实验中讲到了windows验证的两种模式分别是NTLM和Kerberos,那么他们有何区别,在功能上又有何不同。
NTLM是一种比较简单的方法,能够在大部分情况下完成任务。但是它只能完成单跃点认证(只有一个客户端和一个SQL Server服务器)。有些情况下有双跃点(double hop)甚至多跃点的认证需求,这时候就需要用到Kerberos技术。例如,一个用户利用IE浏览器访问有数据库连接脚本的网页,连接配置为使用它自己的Windows账号建立。这时候就需要IIS对这个用户运行IE浏览器的安全上下文(Security Context)首先做认证。通过认证后,再将它传递到SQL Server服务上,SQL Server服务再次认证,确认它有访问SQL Server数据库的权力。这个在IIS服务上完成的身份传递,我们称为双跃点,或者是Delegation(委托)(由客户端委托IIS做身份的传递)。还有一种常见的情况,就是在SQL Server上建立一个链接服务器(Linked Server),当配制安全的时候,选择的是使用当前用户的安全上下文登录目标链接服务器(Be made using the login’s current security context)(见图5-24)。在这种选择下,本地的SQL Server也会做一次双跃点,把客户端的安全上下文传递到远端的SQL Server服务器上。
正文
本文主要讲解如何配置delegation,delegation的前提条件就是已经配置好了Kerberos验证,具体方法参考前一篇博客SQL Kerberos的原理及实验。
实验环境还是前面的提到的三台机器,分别是DC->SANZ-W7(做跃迁节点)->WUW-W7。其中SANZ-W7使用local system启动sql server服务,而WUW-W7使用域账户wuwang启动sql server服务。之所以提到这一点,是因为我们在后面会看到使用WUW-W7做跃迁节点的时候,在DC上做delegation查询时会报错,而使用SANZ-W7做跃迁节点却成功,具体报错内容如下:
Login failed for user ‘NT AUTHORITY\ANONYMOUS LOGON’.
下面我们讲解如何配置delegation,kerberos配置省略。
步骤1:
首先在DC中的computer找到DC,SANZ-W7和WUW-W7,将其配置成“Trust this computer for delegation to any service (Kerberos only)”,如下图所示:
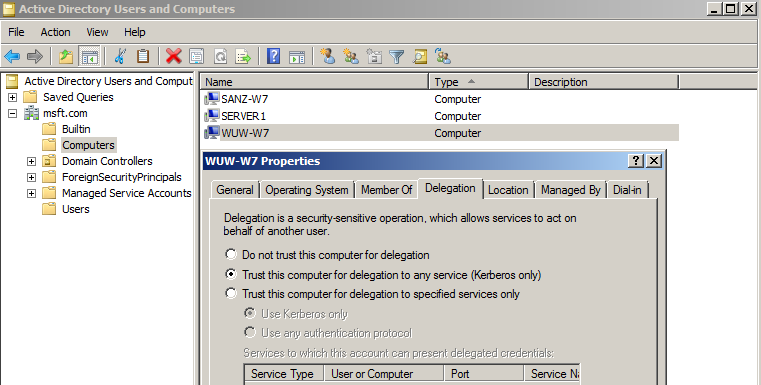
步骤2:
将DC上用户进行delegation查询的域账户administrator的“Account is sensitive and cannot be delegated”属性关闭,也就是不选,如下图所示:
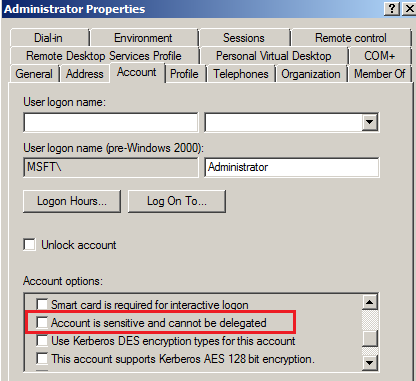
步骤3:
回到DC上,验证SPN已经在了,我的域名是msft,我们在命令行中执行如下命令:
ldifde -d "CN=Users,DC=toppest,DC=com" -l servicePrincipalName -F output.txt
执行结果如下图所示:
然后我们可以在C:\Users\Administrator下找到这个output.txt文件。然后确认SQL Server的启动账号wuwang下,有两个SQL Server的SPN,并且没有其他账户注册相同的SPN。
dn: CN=Wu Wang,CN=Users,DC=msft,DC=com
changetype: add
servicePrincipalName: MSSQLSvc/WUW-W7.msft.com:1433
servicePrincipalName: MSSQLSvc/WUW-W7.msft.com
我在自己的output.txt文件中确实找到了如下信息,但是没有找到sanzhang这个域账户的信息,只有如下所示的spn信息
dn: CN=San Zhang,CN=Users,DC=msft,DC=com
changetype: add
这可能就是使用域账户启动服务和使用local system启动sql server的区别吧。也真是因为在output.txt中没有sanzhang的spn注册信息,所以才有前面提到的不能使用WUW-W7作为跃迁节点。因为DC在进行delegation的时候,最后一个节点必须是域账户注册spn的,也就是能够在output.txt上找到spn信息的节点。
步骤4
在DC的找到wuwang和sanzhang账号,确认它在Delegation这个选项卡里,选择了“Trust this user for delegation to any service (Kerberos only)”,我发现我这里只有wuwang账户有delegation选项,如下图所示:
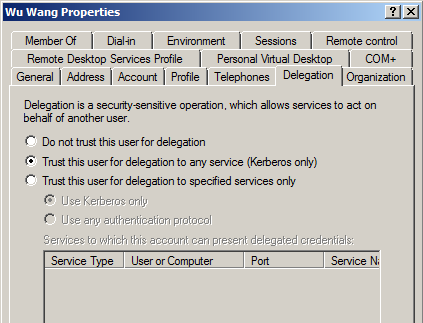
步骤5
我们在跃迁节点SANZ-W7上建立一个连接服务器Linked Server,用来连接WUW-W7这个服务器,创建连接服务器的sql代码如下所示:
Exec sp_dropserver WANGWU
EXEC sp_addlinkedserver
@server='WANGWU',
@srvproduct='',
@provider='SQLOLEDB',
@datasrc='WUW-W7'
select * from WANGWU.InsideTSQL2008.HR.Employees
select * from WANGWU.InsideTSQL2008.Sales.Orders
步骤6
我们要进行delegation,相当于是DC通过SANZ-W7来访问WUW-W7,所以我们必须在WUW-W7中将DC的用户administrator添加到windows验证的login中,并且赋予查询测试数据库InsideTSQL2008的权限。
如果你的DC没有安装sql server,你只需要安装sql server native client和sqlcmd就可以连接数据库了,具体方法参考博客:SQL Server native client与sqlcmd单独安装 。
在DC中使用sqlcmd连接跃迁节点SANZ-W7,连接代码如下:
sqlcmd -S SANZ-W7 -E
此时我们去查看SANZ-W7的安全日志(Event View->Windows log->Security),我们会发现有一个从DC\Administrator的访问,并且使用Kerberos验证,如下图所示:
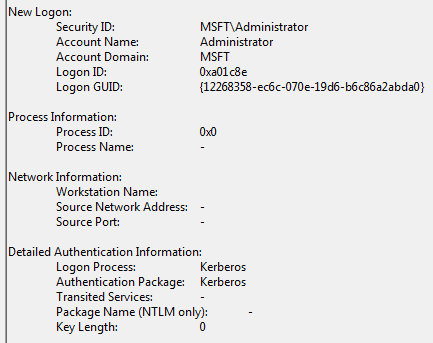
接着我们通过链接服务器连接WUW-W7这个数据库,代码如下图所示:

运行完上述命令以后会得到查询结果,彼此我们去查看WUW-W7的安全日志,会发现多了一条从administrator过来的kerberos验证登陆,跟前面的安全日志一样。
综上,我们就完整了delegation的完整配置。
https://www.cnblogs.com/xwdreamer/category/386469.html