矩阵空间
矩阵空间是对向量空间的扩展,因为矩阵的本质是向量,所以与向量空间类似,也存在矩阵空间。
在向量空间中,任意两个向量的加法和数乘仍然在该空间内。类似的,所有固定大小的矩阵也组成了矩阵空间,在空间内的任意两个矩阵的加法和数乘也在该空间内。例如,M是所有3×3矩阵构成的空间,空间内的矩阵可以相加,也可以数乘,其结果仍然是3×3矩阵。虽然可以把它们中的两个相乘,但是没人会那么做,因为乘法与向量空间没有关系。
看起来我们需要随时注意乘法的概念,线性代数中的乘法有别于中学时代标量间的乘法。向量与一个标量相乘,被明确定义为数乘;两个相同维度的向量间存在点积和叉乘,其写法上都与九九乘法表中的乘法类似,但是没有定义两个向量的乘法。虽然矩阵间定义了乘法,但存在限制,只有满足“攘外必先安内”原则的两个矩阵才能相乘。线性代数中的概念众多,学了线性代数后,再也不能愉快地做乘法了。
“攘外必先安内”:AB两个矩阵相乘,必须满足A的列数等于B的行数:

如果AB能够相乘,必须满足n = p,看起来n和p正好夹在m和q中间,m和q在外围:

相乘的结果当然是“共同御敌,一致对外”。
以3×3矩阵构成的空间M为例,M一共有9个元素,M的维度是9。M的标准基是:

矩阵的子空间
矩阵的子空间也是对向量子空间的扩展,矩阵子空间需要满足数乘和加法仍处于同一集合内。
矩阵空间M也有一些特殊的子空间,比如将M空间内的两个对称矩阵相加或数乘,仍然得到对称矩阵;上三角矩阵子空间,将空间内的两个矩阵相加或数乘,仍然得到上三角矩阵。仍然以3×3矩阵构成的空间M为例,看看M中的几个子空间。
对称矩阵子空间
设M中的对称子空间是S,6个对称矩阵构成了S的标准基:

S维度是6,表示为:
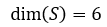
上三角矩阵子空间
设上三角矩阵子空间是U,U的维度也是6,它的维度表示为:

很明显,上三角矩阵的基是:
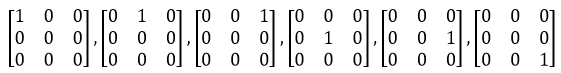
对角矩阵子空间
如果一个矩阵既是对称矩阵又是上三角矩阵,则这个矩阵称为对角矩阵(diagonal matrix)。对称矩阵是一个主对角线之外的元素皆为0的矩阵,常写为diag(λ1, λ2,..., λn)。
主对角线上的元素可以为 0 或其他值,对角线上元素相等的对角矩阵称为数量矩阵;对角线上元素全为1的对角矩阵就是单位矩阵。对角矩阵的运算包括和、差运算、数乘运算、同阶对角阵的乘积运算,且这些运算的结果仍为对角阵。
对角矩阵A:
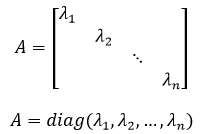
数量矩阵,对称矩阵的对角元线上的元素都相等:
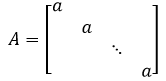
单位矩阵,对称矩阵的对角元线上的元素都为1:
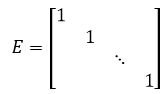
M3×3内的对称矩阵和上三角矩阵的交集是一个对角矩阵,所有对角矩阵也构成一个子空间其维度是3:
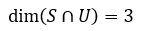
很明显,S∩U的标准基是:

S+U矩阵子空间
对于S∪U,它或者在对称矩阵子空间S中,或者在上三角矩阵子空间U中,或者在对角矩阵子空间S∩U中。我们对S∪U不感兴趣,主要是的原因是S∪U并不能构成子空间,可以随便举个例子:
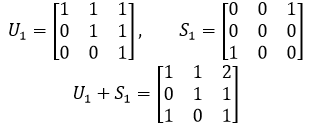
可以看到,U1 + S1是个没什么特点的矩阵,它不属于S∪U,所以不符合子空间的加法封闭性。
现在,我们将S∪U扩大一点,变成S + U,也就是不单独地取S和U中的矩阵,而是取S中的任一矩阵和U中的任一矩阵,将二者相加:
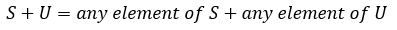
其结果是整个M空间,即:
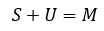
当然,S + U的维数也是M的维数:
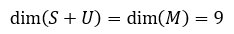
矩阵子空间维数的关系
现在将上面4个矩阵子空间的维数放在一起:
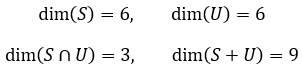
可以看出:

秩1矩阵
秩1矩阵就是秩为1的矩阵,它的行空间和列空间的维度都是1:
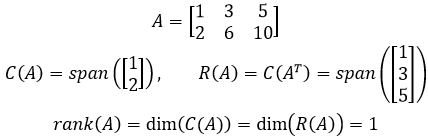
更进一步,秩1矩阵可以表示为一列乘以一行的形式:

我们之所以对秩1矩阵感兴趣,是因为可以通过秩1矩阵搭建出任意矩阵,比如秩为4的矩阵,可以通过4个秩1矩阵搭建而成。
如果M是所有5×10矩阵的矩阵空间,那么一个由秩4矩阵组成的子集是否是一个子空间?
当然不是,因为两个矩阵之和的秩不大于两个矩阵的秩之和。设P是M中两个任意秩4矩阵之和,P的秩可能是5,不在秩4矩阵集合内。虽然P是两个秩4矩阵之和,rank(P) ≤4 + 4 = 8,但由于P仍然在M5×10内,而M5×10中的矩阵的秩不会大于5,所以rank(P)的最大值是5。同理,M中由秩1矩阵组成的子集也不是子空间。
秩1矩阵与零空间的关系
假设有一个向量x,x中的分量之和为0:
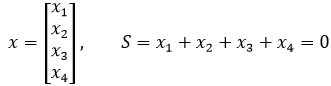
很明显x满足零空间的条件,它是某个矩阵的零空间,这个矩阵是什么呢?也就是说对于Ax = 0来说,A是什么?x的维数又是什么?
先回答最后一个,根据条件S可以确定,x的一个分量可以由另外三个分量表示:
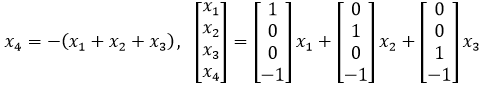
可见x的主变量有1个,自由变量有3个,维数是3。
再看零空间所属的矩阵,可以很容易判断:

A是秩1矩阵,根据《线性代数14——行空间和左零空间》空间和维数的关系:Am×n的零空间是位于Rn下的 n – r维空间,A的零空间的维数3,x是3维的。
A的列空间和行空间都是1维的:
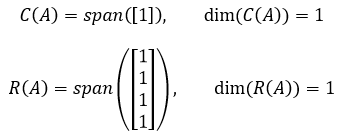
A的左零空间是零向量。
作者:我是8位的
出处:http://www.cnblogs.com/bigmonkey
本文以学习、研究和分享为主,如需转载,请联系本人,标明作者和出处,非商业用途!
扫描二维码关注公众号“我是8位的”