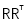一、对称函数

    在对称函数中，函数的输出值不随输入变数的排列而改变。从函数的形式中可以看出若输入变数排列后，方程式不会改变。例如对于一个球体．若 φ 为其方位角，θ为其天顶角，r为半径，则大圆距离可以表示为

根据上述的距离公式，可以看出一些对称性，在以下变换下，距离不变：

天顶角各加某特定角度。

其方位角对调、天顶角对调，或是两者都对调。

 

二、半正定矩阵

A．常用定义

设A为实对称矩阵，若对于每个非零实向量X，都有X'AX≥0，则称A为半正定矩阵，称X'AX为半正定二次型。（其中，X'表示X的转置）

1）设A为实对称矩阵，若对于每个非零实向量X，都有X'AX>0，则称A为正定矩阵，称X'AX为正定二次型。

2）设A为实对称矩阵，若对于每个非零实向量X，都有X'AX<0，则称A为负定矩阵，称X'AX为负定二次型。

3） 设A为实对称矩阵，若对于每个非零实向量X，都有X'AX≤0，则称A为半负定矩阵，称X'AX为半负定二次型。

4）设A为实对称矩阵，若A既不是半正定又不是半负定，则称A为不定矩阵，称X'AX为不定二次型。

5） 设A为Hermite矩阵，若对于每个非零复向量X，都有X*AX≥0，则称A为半正定复矩阵。（其中，X*表示X的共轭转置）

B．性质

1.半正定矩阵的行列式是非负的。

2.两个半正定矩阵的和是半正定的。

3.非负实数与半正定矩阵的数乘矩阵是半正定的。

C．判定

设A是n阶实对称矩阵，则下列的条件等价：

1.A是半正定的。

2.A的所有主子式均为非负的。

3.A的特征值均为非负的。

4.存在n阶实矩阵C，使A=C′C.

5.存在秩为r的r×n实矩阵B，使A=B′B.