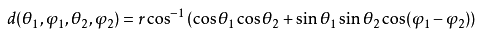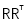今天要介绍一种新的向量空间，即矩阵空间，之前碰到的所有向量空间，都是n维的实数空间，现在我们将矩阵当成向量，比如说将3*3的矩阵看作向量，这相当于从原来的n维为扩展到n*n维，那么明明是矩阵为什么可以看成是向量呢？因为矩阵也服从向量空间的运算，向量能相加，矩阵也能相加，向量能数乘，矩阵也可以数乘，向量可以线性组合，矩阵也可以线性组合。所以说矩阵也可以当成向量来生成空间，这个空间就是矩阵空间。比如说所有3*3的矩阵组成的空间，我们记为矩阵空间M，那么M的子空间有：所有上三角矩阵（upper triangular matrix）组成的空间U、所有的对称矩阵（symmetricmatrix）组成的空间S，所有的对角矩阵（diagonal matrix）组成的空间D（对角矩阵是上三角阵和对称阵的交集），因为两个上三角阵相加还是上三角阵，两个对称阵相加还是对称阵，两个对角阵相加还是对角阵，除此之外，我们还可以得出M空间的维数是9，9个基分别为：
S空间的维数是6，6个基分别为：
U空间的维数也是6，基分别为：
通过将U和S进行组合，我们还可以得到其他子空间，比如前面已经提过的对称阵空间S和上三角阵空间U的交集 
得到的对角阵空间D，其维数是3维，但是注意并集 组成的集合不是子空间，要将
符号改成“+”，即S+U才构成子空间，如果每次任取S内任一元素加上U内任一元素，我们可以得到所有3*3矩阵，因此这个S+U构成的空间维度是9，这里我们可以发现dim(S)+dim(U)=dim(S交U)+dim(S+U)，即S的维度加上U的维度等于它们交的维度加上它们和的维度，以上就是关于矩阵空间的内容，除了向量跟传统的向量有区别，其他都是一样的求法。现在我们再举个比较特殊的例子，假设有一个矩阵空间，它来自于微分方程，该微分方程为d2y/dx2+y=0，其解是y=cos( x) ，y=sin( x)，这个微分方程的零空间或解空间就是这两个解的线性组合，也就是y=c1cos(x)+c2sin(x)，很铭明显这个向量空间的维数是2，因为它有2个基：cos(x)和sin(x)。举这个例子的目的在于：cos(x)和sin(x)看起来并不像向量，有些像函数，但我们可以称它们为向量，因为其可以做数乘也可以作加法，所以可对它们进行线性组合，这就是线性代数中的向量，基，维数，它们不仅仅局限于我们平常所熟悉的向量形式，也可以用于矩阵甚至函数等，只要它们满足向量的特性。
秩1矩阵
关于矩阵的秩r，目前我们已经知道的是它等于矩阵主元的个数，且r<m，r<n，秩1矩阵是一类性质很好但非常简单的矩阵，因此我们在这里对其作一些简单分析。假设现有秩1矩阵
，经过消元可得知其行空间的基为A的第一行，列空间的基为A的第一列，那么A可以写成两个基相乘的形式，即
，对于所有的秩1矩阵，这个结论都是成立的，即所有的秩1矩阵都能表示为一列基乘以一行基的形式A=UVT，秩1矩阵就像搭其它矩阵的积木，任何矩阵都可以表示为若干个秩1矩阵的组合，例如如果有一个5*17的矩阵，它的秩为4，那么这个矩阵就可分解为4个秩1矩阵的组合。
