1、模式定义
委托是对一个类的功能进行扩展和复用的方法。它的做法是:写一个附加的类提供附加的功能,并使用原来的类的实例提供原有的功能。 假设我们有一个 TeamLead 类,将其既定任务委托给一个关联辅助对象 JuniorDeveloper 来完成:本来 TeamLead 处理 writeCode 方法,Usage 调用 TeamLead 的该方法,但现在 TeamLead 将 writeCode 的实现委托给 JuniorDeveloper 的 writeBadCode 来实现,但 Usage 并没有感知在执行 writeBadCode 方法。
2、UML类图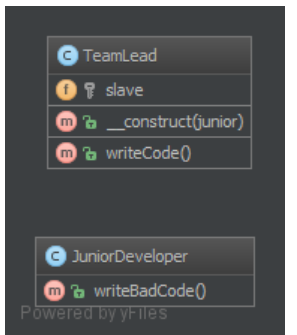
3、示例代码
Usage.php
<?phpnamespace DesignPatterns\More\Delegation;// 初始化 TeamLead 并委托辅助者 JuniorDeveloper
$teamLead = new TeamLead(new JuniorDeveloper());// TeamLead 将编写代码的任务委托给 JuniorDeveloper
echo $teamLead->writeCode();
TeamLead.php
<?phpnamespace DesignPatterns\More\Delegation;/*** TeamLead类* @package DesignPatterns\Delegation* `TeamLead` 类将工作委托给 `JuniorDeveloper`*/
class TeamLead
{/** @var JuniorDeveloper */protected $slave;/*** 在构造函数中注入初级开发者JuniorDeveloper* @param JuniorDeveloper $junior*/public function __construct(JuniorDeveloper $junior){$this->slave = $junior;}/*** TeamLead 喝咖啡, JuniorDeveloper 工作* @return mixed*/public function writeCode(){return $this->slave->writeBadCode();}
}
JuniorDeveloper.php
<?phpnamespace DesignPatterns\More\Delegation;/*** JuniorDeveloper 类* @package DesignPatterns\Delegation*/
class JuniorDeveloper
{public function writeBadCode(){return "Some junior developer generated code...";}
}
4、测试代码
Tests/DelegationTest.php
<?phpnamespace DesignPatterns\More\Delegation\Tests;use DesignPatterns\More\Delegation;/*** DelegationTest 用于测试委托模式*/
class DelegationTest extends \PHPUnit_Framework_TestCase
{public function testHowTeamLeadWriteCode(){$junior = new Delegation\JuniorDeveloper();$teamLead = new Delegation\TeamLead($junior);$this->assertEquals($junior->writeBadCode(), $teamLead->writeCode());}
}