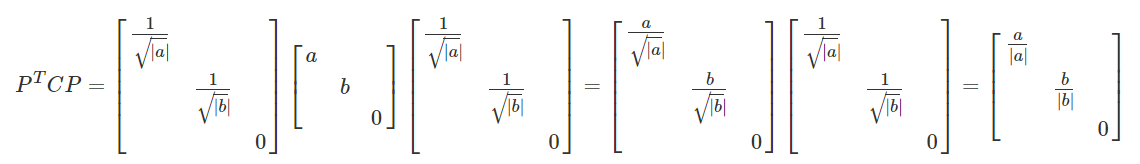前言
本文主要针对线性代数中的正定矩阵、实对称矩阵、矩阵特征值分解以及矩阵 SVD 分解进行总结。
如果你对这篇文章感兴趣,可以点击「【访客必读 - 指引页】一文囊括主页内所有高质量博客」,查看完整博客分类与对应链接。
正定矩阵
1. 概念
首先正定矩阵是定义在对称矩阵的基础上,其次对于任意非零向量 x \textbf{x} x,若 x T A x > 0 \textbf{x}^T\textbf{\textit{A}}\textbf{x}>0 xTAx>0 恒成立,则矩阵 A \textbf{\textit{A}} A 为正定矩阵;若 x T A x ≥ 0 \textbf{x}^T\textbf{\textit{A}}\textbf{x}\geq 0 xTAx≥0 恒成立,则矩阵 A \textbf{\textit{A}} A 为半正定矩阵。
2. 物理意义
任意非零向量 x \textbf{x} x 经过矩阵 A A A 线性变换后,与原先向量的夹角 ≤ 90 \leq 90 ≤90 度。
3. 其他充要条件
充要条件1:矩阵 A \textbf{\textit{A}} A 的全部特征值都是正数推论:若 A \textbf{\textit{A}} A 正定,则 ∣ A ∣ > 0 |\textbf{\textit{A}}|>0 ∣A∣>0,即 A \textbf{\textit{A}} A 可逆(有时会根据矩阵正定来判断是否可逆)推论:若 A \textbf{\textit{A}} A 正定,则 A \textbf{\textit{A}} A 与单位阵合同,即存在可逆阵 C \textbf{\textit{C}} C,使得 C T AC = E \textbf{\textit{C}}^T\textbf{\textit{A}}\textbf{\textit{C}}=\textbf{\textit{E}} CTAC=E 成立
充要条件2:矩阵 A \textbf{\textit{A}} A 的各阶顺序主子式都是正数,即 Δ i > 0 \Delta_i>0 Δi>0- 其中 Δ i \Delta_i Δi 表示矩阵 A \textbf{\textit{A}} A 前 i i i 行与前 i i i 列组成的子矩阵的行列式的值
- 推论: ∣ A ∣ > 0 |A|>0 ∣A∣>0 则 A A A 一定可逆
实对称矩阵
1. 概念
矩阵为方阵,其中元素均为实数,且 A = A T \textbf{\textit{A}}=\textbf{\textit{A}}^T A=AT。
2. 性质
性质1:实对称矩阵的特征值都是实数。- 假设 λ \lambda λ、 x \textbf{x} x 分别为矩阵 A \textbf{\textit{A}} A 的特征值、特征向量,即 A x = λ x \textbf{\textit{A}}\textbf{x}=\lambda \textbf{x} Ax=λx
- 等式两边取共轭,即 a + b i ‾ = a − b i \overline{a+bi}=a-bi a+bi=a−bi, A ‾ x ‾ = λ ‾ x ‾ \overline{\textbf{\textit{A}}}\overline{\textbf{x}}=\overline{\lambda} \overline{\textbf{x}} Ax=λx, A \textbf{\textit{A}} A 是实对称矩阵,因此 A = A T = A ‾ \textbf{\textit{A}}=\textbf{\textit{A}}^T=\overline{\textbf{\textit{A}}} A=AT=A,即 A x ‾ = λ ‾ x ‾ \textbf{\textit{A}}\overline{\textbf{x}}=\overline{\lambda} \overline{\textbf{x}} Ax=λx
- 等式两边取转置,则 x T A = λ x T \textbf{x}^T\textbf{\textit{A}}=\lambda \textbf{x}^T xTA=λxT
- x T A x ‾ = λ ‾ x T x ‾ = λ x T x ‾ \textbf{x}^T\textbf{\textit{A}}\overline{x}=\overline{\lambda}\textbf{x}^T\overline{\textbf{x}}=\lambda \textbf{x}^T\overline{\textbf{x}} xTAx=λxTx=λxTx
- ( λ − λ ‾ ) ∥ x ∥ 2 2 = 0 (\lambda-\overline{\lambda})\left\|\textbf{x}\right\|_2^2=0 (λ−λ)∥x∥22=0,由于 ∥ x ∥ 2 2 > 0 \left\|\textbf{x}\right\|_2^2>0 ∥x∥22>0,因此 λ = λ ‾ \lambda=\overline{\lambda} λ=λ, λ \lambda λ 为实数
性质2:实对称矩阵不同特征值所对应的特征向量必定正交。- 假设 A x 1 = λ 1 x 1 \textbf{\textit{A}}\textbf{x}_1=\lambda_1 \textbf{x}_1 Ax1=λ1x1 与 A x 2 = λ 2 x 2 \textbf{\textit{A}}\textbf{x}_2=\lambda_2 \textbf{x}_2 Ax2=λ2x2 成立
- x 1 T A = λ 1 x 1 T \textbf{x}_1^T\textbf{\textit{A}}=\lambda_1 \textbf{x}_1^T x1TA=λ1x1T
- x 1 T A x 2 = λ 1 x 1 T x 2 = λ 2 x 1 T x 2 \textbf{x}_1^T\textbf{\textit{A}}\textbf{x}_2=\lambda_1 \textbf{x}_1^T\textbf{x}_2=\lambda_2\textbf{x}_1^T\textbf{x}_2 x1TAx2=λ1x1Tx2=λ2x1Tx2
- ( λ 1 − λ 2 ) x 1 T x 2 = 0 (\lambda_1-\lambda_2)\textbf{x}_1^T\textbf{x}_2=0 (λ1−λ2)x1Tx2=0,因此 x 1 \textbf{x}_1 x1 与 x 2 \textbf{x}_2 x2 正交
性质3:实对称矩阵相同特征值所对应的特征向量必定线性无关。- 证明较繁琐,不详细展开
- 线性无关的向量可以通过施密特正交化转为正交向量
- 对于线性无关向量组 x 1 , x 2 , . . . , x n \textbf{x}_1,\textbf{x}_2,...,\textbf{x}_n x1,x2,...,xn,转为正交向量组 y 1 , y 2 , . . . , y n \textbf{y}_1,\textbf{y}_2,...,\textbf{y}_n y1,y2,...,yn
- y 1 = x 1 \textbf{y}_1=\textbf{x}_1 y1=x1
- y i = x i − ∑ j = 1 i − 1 x i T y j y j T y j y j \textbf{y}_i=\textbf{x}_i-\sum\limits_{j=1}^{i-1}\displaystyle\frac{\textbf{x}_i^T\textbf{y}_j}{\textbf{y}_j^T\textbf{y}_j}\textbf{y}_j yi=xi−j=1∑i−1yjTyjxiTyjyj
- 由于新的正交向量都是原来线性无关向量的线性组合,而原先的线性无关向量对应的特征值均相同,因此新的正交向量也均为该相同特征值对应的特征向量
性质4:任何一个实对称矩阵,都可以正交对角化。- 正交对角化,即存在一个正交矩阵 Q ( Q T = Q − 1 ) \textbf{\textit{Q}}(\textbf{\textit{Q}}^T=\textbf{\textit{Q}}^{-1}) Q(QT=Q−1) 使得 Q T AQ = D \textbf{\textit{Q}}^T\textbf{\textit{A}}\textbf{\textit{Q}}=\textbf{\textit{D}} QTAQ=D,其中 D \textbf{\textit{D}} D 是一个对角矩阵
- 实对称矩阵,一定有 n n n 个解,因为实对称矩阵特征值都是实数,因此一共有 n n n 个实特征值(包括重特征值)—— 性质 1 1 1
- 不同特征值对应的特征向量正交,相同特征值也一定存在对应的正交向量 —— 性质 2 , 3 2,3 2,3
- 实对称矩阵,一定有 n n n 个正交特征向量,因此可以特征值分解,即该性质成立
性质5:实对称矩阵的非零特征值个数等于矩阵的秩- 矩阵 A \textbf{\textit{A}} A 相似于对角矩阵, P − 1 AP = D \textbf{\textit{P}}^{-1}\textbf{\textit{A}}\textbf{\textit{P}}=\textbf{\textit{D}} P−1AP=D
- 对角矩阵 D \textbf{\textit{D}} D 的秩 = 矩阵 A \textbf{\textit{A}} A 的秩 = D \textbf{\textit{D}} D 非零特征值个数
- 矩阵 A \textbf{\textit{A}} A 与 矩阵 D \textbf{\textit{D}} D 相似,则特征值相同
性质6:实对称矩阵不一定可逆,但若可逆,则一定是实对称矩阵- 0 矩阵对称不可逆
- ( A − 1 ) T = ( A T ) − 1 = A − 1 (A^{-1})^T=(A^T)^{-1}=A^{-1} (A−1)T=(AT)−1=A−1
矩阵特征值分解
1. 概念
n ∗ n n*n n∗n 的方阵 A \textbf{\textit{A}} A,由 A x = λ x \textbf{\textit{A}}\textbf{x}=\lambda \textbf{x} Ax=λx 可以得到 AV = V Λ \textbf{\textit{A}}\textbf{\textit{V}}=\textbf{\textit{V}}\Lambda AV=VΛ。
- 如果方阵 A \textbf{\textit{A}} A 有 n n n 个线性无关的特征向量,则 V \textbf{\textit{V}} V 可逆
- A = V Λ V − 1 \textbf{\textit{A}}=\textbf{\textit{V}}\Lambda\textbf{\textit{V}}^{-1} A=VΛV−1
- 其中矩阵 V \textbf{\textit{V}} V 的列为方阵 A \textbf{\textit{A}} A 的特征向量, Λ = d i a g ( λ 1 , λ 2 , . . . , λ n ) , λ i ≥ λ i + 1 \Lambda=diag(\lambda_1,\lambda_2,...,\lambda_n),\lambda_i\geq \lambda_{i+1} Λ=diag(λ1,λ2,...,λn),λi≥λi+1
矩阵 SVD 分解
1. 概念
任意一个矩阵 A \textbf{\textit{A}} A 都可以分解为 A = U Σ V T \textbf{\textit{A}}=\textbf{\textit{U}}\Sigma\textbf{\textit{V}}^T A=UΣVT,其中 U , V \textbf{\textit{U}},\textbf{\textit{V}} U,V 均为正交单位矩阵, Σ \Sigma Σ 为对角矩阵。
2. 证明
- A T A = ( U Σ V T ) T U Σ V T = V Σ 2 V T \textbf{\textit{A}}^T\textbf{\textit{A}}=(\textbf{\textit{U}}\Sigma\textbf{\textit{V}}^T)^T\textbf{\textit{U}}\Sigma\textbf{\textit{V}}^T=\textbf{\textit{V}}\Sigma^2\textbf{\textit{V}}^T ATA=(UΣVT)TUΣVT=VΣ2VT,由于 A T A \textbf{\textit{A}}^T\textbf{\textit{A}} ATA 为实对称矩阵,因此 V \textbf{\textit{V}} V 为矩阵 A T A \textbf{\textit{A}}^T\textbf{\textit{A}} ATA 对应特征向量组成的正交单位阵。
- A A T = U Σ V T ( U Σ V T ) T = U Σ 2 U T \textbf{\textit{A}}\textbf{\textit{A}}^T=\textbf{\textit{U}}\Sigma\textbf{\textit{V}}^T(\textbf{\textit{U}}\Sigma\textbf{\textit{V}}^T)^T=\textbf{\textit{U}}\Sigma^2\textbf{\textit{U}}^T AAT=UΣVT(UΣVT)T=UΣ2UT,由于 A A T \textbf{\textit{A}}\textbf{\textit{A}}^T AAT 为实对称矩阵,因此 U \textbf{\textit{U}} U 矩阵 A A T \textbf{\textit{A}}\textbf{\textit{A}}^T AAT 对应特征向量组成的正交单位阵。
- AV = U Σ \textbf{\textit{A}}\textbf{\textit{V}}=\textbf{\textit{U}}\Sigma AV=UΣ,其中 Σ \Sigma Σ 为对角阵,因此 A v i = σ i u i \textbf{\textit{A}}\textbf{v}_i=\sigma_i\textbf{u}_i Avi=σiui,由此可以得到对角矩阵 Σ \Sigma Σ,其中 σ i \sigma_i σi 就是奇异值。
- A m ∗ n = U m ∗ m Σ m ∗ n V n ∗ n T \textbf{\textit{A}}_{m*n}=\textbf{\textit{U}}_{m*m}\Sigma_{m*n}\textbf{\textit{V}}_{n*n}^T Am∗n=Um∗mΣm∗nVn∗nT
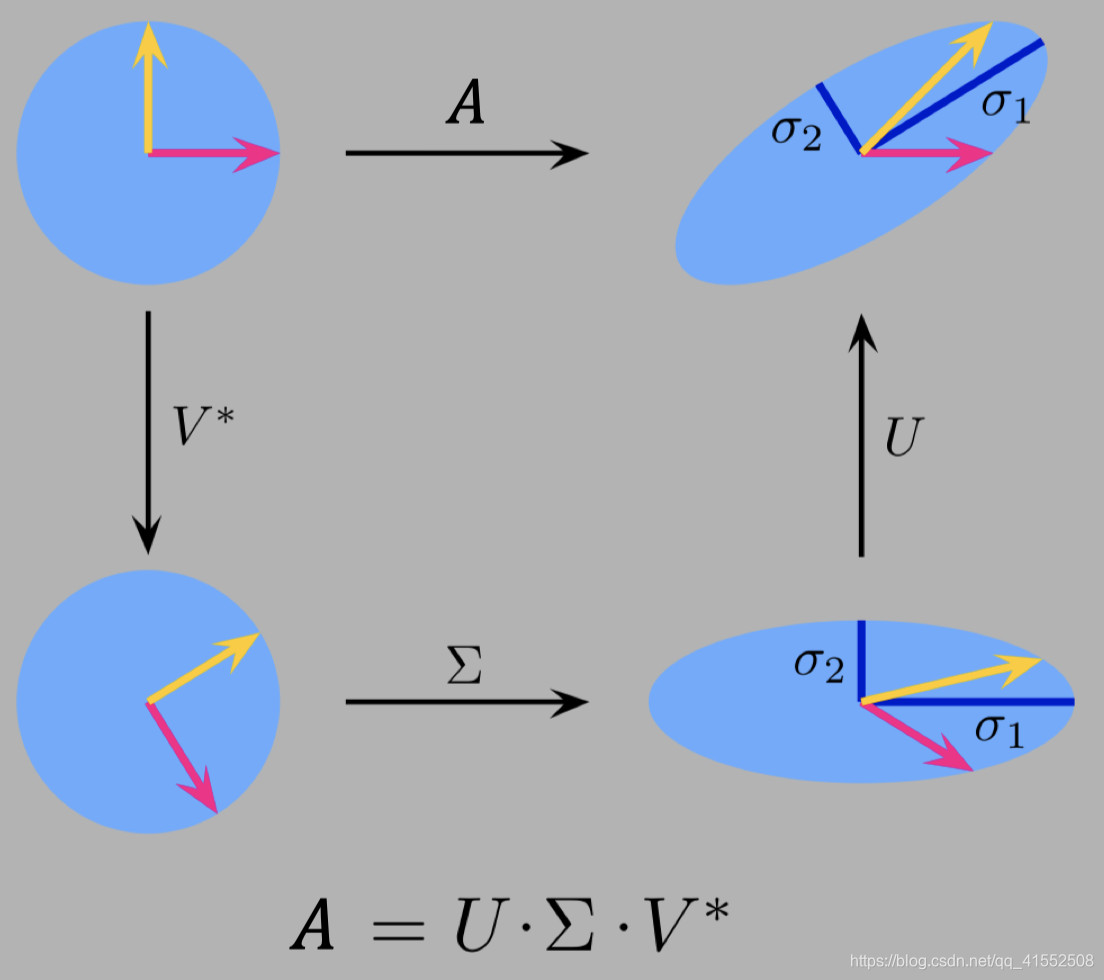
3. 几何角度
矩阵 U , V U,V U,V 仅负责旋转, Σ \Sigma Σ 负责放缩,具体示意图如下:
4. SVD 压缩
如下所示,仅选取前 r r r 个不为零的奇异值,可以实现无损压缩。注意非零奇异值的个数等于矩阵 A A A 的秩。

5. 计算伪逆

6. Eckart-Young Theorem
如果矩阵 B \mathbf{B} B 的秩为 k k k,则 ∣ ∣ A − B ∣ ∣ ≥ ∣ ∣ A − A k ∣ ∣ ||A-B||\geq||A-A_k|| ∣∣A−B∣∣≥∣∣A−Ak∣∣ 对如下三个矩阵范数成立:
- ∣ ∣ A ∣ ∣ 2 = σ 1 ||A||_2=\sigma_1 ∣∣A∣∣2=σ1,即最大的奇异值
- ∣ ∣ A ∣ ∣ N u c l e a r = ∑ i = 1 r σ i ||A||_{Nuclear}=\sum\limits_{i=1}^r\sigma_i ∣∣A∣∣Nuclear=i=1∑rσi
- Frobenius norm = ∣ ∣ A ∣ ∣ 2 , 1 = ∣ ∣ A ∣ ∣ F = ( t r ( A T A ) ) 1 / 2 = ( ∑ i = 1 m ∑ j = 1 n a i j 2 ) 1 / 2 =||A||_{2,1}=||A||_F=(tr(A^TA))^{1/2}=(\sum\limits_{i=1}^m\sum\limits_{j=1}^na_{ij}^2)^{1/2} =∣∣A∣∣2,1=∣∣A∣∣F=(tr(ATA))1/2=(i=1∑mj=1∑naij2)1/2
其中 A \mathbf{A} A 与 A k \mathbf{A_k} Ak 定义如下:
A = U Σ V T = ∑ i = 1 r σ i u i v i T A k = U k Σ k V k T = ∑ i = 1 k σ i u i v i T \begin{aligned} & \mathbf{A}=\mathbf{U}\Sigma\mathbf{V}^T=\sum\limits_{i=1}^r \sigma_i\mathbf{u}_i\mathbf{v}_i^T\\ & \mathbf{A}_k=\mathbf{U}_k\Sigma_k\mathbf{V}_k^T=\sum\limits_{i=1}^k \sigma_i\mathbf{u}_i\mathbf{v}_i^T \end{aligned} A=UΣVT=i=1∑rσiuiviTAk=UkΣkVkT=i=1∑kσiuiviT
需要注意,矩阵乘上一个正交矩阵,其奇异值不会发生变化,即上述涉及的矩阵范数不会改变。
7. LSI
计算不同 q u e r y query query 之间的相似程度,常用于推荐系统。

更多 SVD 的应用:
- 为数据集推荐算法模型
- 推荐系统、图像去噪等