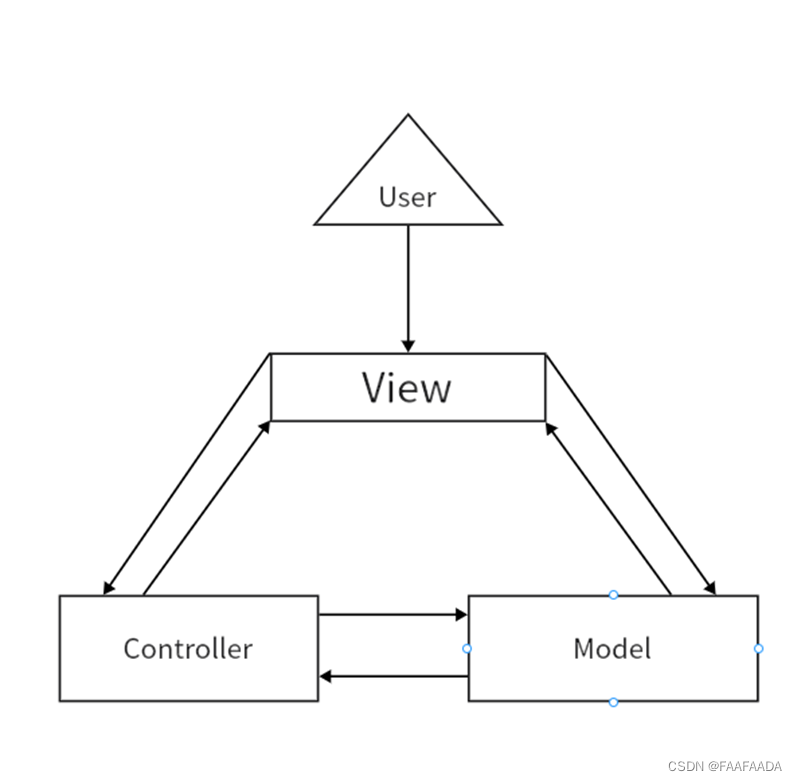
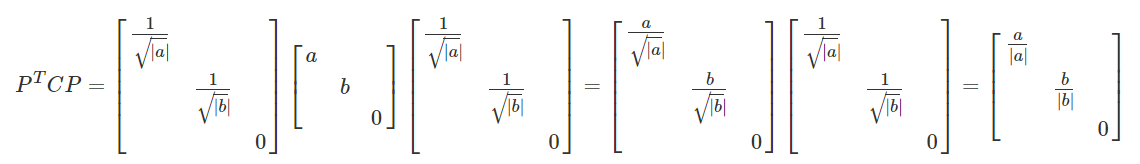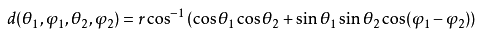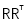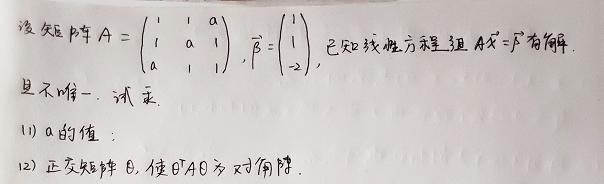用委托机制（delegation）来定制行为

应用程序的委托是Cocoa最重要的设计模式——委托机制的一个例子。

委托机制的想法在于：一个对象能有单一的委托对象，可以在某些事件发生的时候调用它。从委托的角度来看，这就是某种回调或者通知机制：“在这件事发生时调用我”。从其委托的对象的角度来看，它更像是推卸责任：“我不知道在事件发生时有什么需要做的，所以你来对付它”。

就应用程序委托来说，UIApplicationMain中声明为应用程序委托的对象在各种影响整个应用程序的事件发生时得到回调：在应用程序从主屏幕上开始运行时，当它和一个URL一起被另一个应用启动时（见第26章），在应用程序被警告内存不足时等。这是正式委托安排的一个例子，而这个是由一种Objective-C协议——UIApplicationDelegate所定义的。这个协议像一个正式的Cocoa类那样有它自己的文档页面，但是不同的是它描述了什么时候委托方法会被调用，在被调用时作为这些方法的实现者能够或者应当做些什么，而不是描述一个类的方法怎么工作。对于一个成为应用程序委托的类来说，它需要在它的头文件中声明它实现了这个协议，然后实现所有没有被标记为“可选的（optional）”的方法。

有一些委托协议是我们可以加到Hello User中去的。这能使它的行为更像一个典型的iPhone应用程序。例如，你会注意到在运行应用程序时，在单击了“Say Hello”按钮之后，键盘不会消失，而且Return键什么都不做。这些对iPhone应用程序来说是常见的任务，并且后者需要我们给文本框提供一个委托。

要去掉键盘，你需要告诉文本框放弃它作为“第一响应对象”的角色。第一响应对象的意思是指这个组件能第一个接收到用户的输入。在按钮被触碰时很容易做这个，只须把下面这行代码加到sayHello:的最后。

但是在Return键被按下时，我们又该怎么做呢？这不是一个来自于任何GUI组件的按钮——键盘是由文本框自动提供的——因此似乎没法把一个事件处理方法跟它绑定。可是，如果你去翻阅一下UITextField的文档^[8]，就会看到它有一个delegate属性，这个delegate属性由UITextFieldDelegate协议所定义，而这个协议是由一组相关联的方法所定义的。查看一下这个协议，你会看到有许多方法用来提醒委托有文本框相关的事件发生。其中一个是textFieldShouldReturn，这个方法看上去像是我们需要的，因为它可以让我们知道用户什么时候按了Return键。

通过在@interface头上紧随本类所扩展的类名称之后的尖括号中指明委托的名称，你可以指明一个对象要实施部分或者全部委托的方法。^[9]对我们来说，HelloUserViewController就是一个好的选择，这是因为它已经知道文本框了。因此，编辑HelloUserViewController.h头文件并在尖括号里增加协议声明到类定义上，就声明了该类要实现的委托协议，如下所示。

现在需要把视图控制器设置成为文本框的委托。可以用代码来做这个，但是既然GUI的其他部分都是在Interface Builder中定义的，同样在IB中设置委托也是有意义的。双击HelloUserViewConroller.xib，在IB中打开它。右键单击文本框，或者用其Connections Inspector，可以看到有一个空的连接叫做delegate。从圆圈连接点拖曳到File's Owner（因为它是被指派为拥有这个nib的对象，因此它代表HelloUser ViewController），这样就声明了HelloUserViewController作为文本框的委托。请在退出IB前确保已经保存。

在视图控制器设置成为文本框的委托后，它就能得到来自文本框的事件驱动回调。现在只须为感兴趣的回调提供实现就行了。

这里是一个简单的方法，用来去掉键盘，可以把它放在HelloUserViewController.m中@implementation和@end之间的任何位置。

这个方法的签名需要与委托协议中定义的签名完全一致，因此可能要养成从文档中复制并粘贴的习惯，或者如果选择去看头文件，从那里复制粘贴也一样。

如你所见，这个方法由textField（可以假定是nameField，因为这个应用只有一个文本框）被传送到我们常简单地用来传送消息的resignFirstResponder中去。这会通知文本框它不再接收文本输入了（至少在再次触碰之前不会），将使得文本框去掉虚拟键盘。然后我们返回YES，如同协议中规定的那样，按Return键时需要实现其默认行为。

在Xcode中构建并执行程序，输入一些文本，然后按Return键。你会看到键盘消失了（如果没有，请检查有没有在IB中把委托连接到File's Owner，以及方法签名是否完全符合上面的代码）。

这个动作不会更新Hello标签，因为更新的代码在sayHello:中，而它只在单击“Say Hello”按钮时才会被调用到。通常情况下想要同样的代码在按钮被单击和按Return键时都调用到的话，可以把这些公共的功能放入一个辅助方法并在两个事件处理方法中都调用它。

可能你已经注意到了，协议的一个好处是只需要定义感兴趣的那些方法就够了。UITextFieldDelegate的所有方法都是可选的（optional），因此可以忽略掉任何不感兴趣的事件。不过也不总是这样的，一些委托协议声明了必需的方法，编译器会强制你实现它们。但这仍是一种方便的模式，一个重要的东西，你会在Cocoa中一次又一次地看到。