1. 人工智能定义

1. 简述什么是人工智能

  人工智能可分为两个维度:一个维度是从思维推理过程到行为结果(过程与结果);另一个维度是与人类表现的逼真度到数学与工程结合后的精确性(主观与客观)。

• 像人—样行动：图灵测试的途径；
• 像人—样思考：认知建模的途径；
• 合理地思考："思维法则"的途径；
• 合理地行动：合理Agent途径；

2. agent判断

2. 考虑一个医疗诊断系统的agent，讨论该agent最合适的种类(简单agent,基于模型的agent,基于目标的agent和基于效用的agent)并解释你的结论

  我认为基于效用的agent最合适，因为医疗诊断系统面对很多不同的人群，存在很多不确定因素，即存在多个目标，多个目标在不确定的环境中。并且，能够治愈病人的方法有很多种，即一个目标有多种行为可以到达，系统必须衡量最优的方法来推荐给病人。所以效率很重要，应该选用基于效用的agent；

3. 搜索树

3. 先建立一个完整的搜索树，起点是S,终点是G,如下图,节点旁的数字表示到达目标状态的距离，然后用以下方法表示如何进行搜索

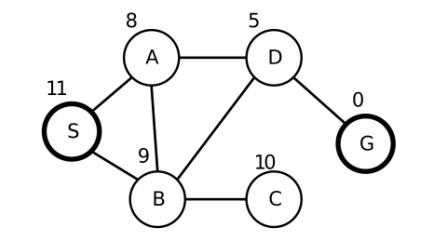
下列图为 ipad 上手绘
建立搜索树：

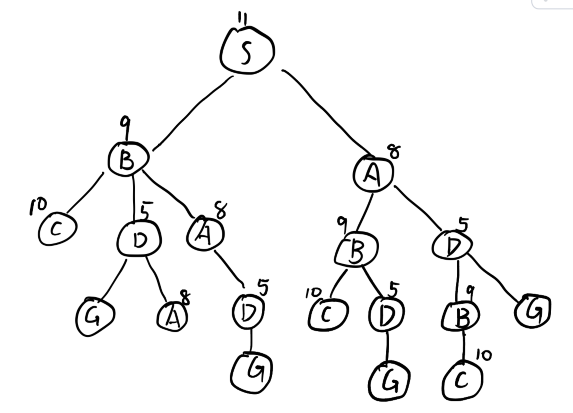
(a).深度优先

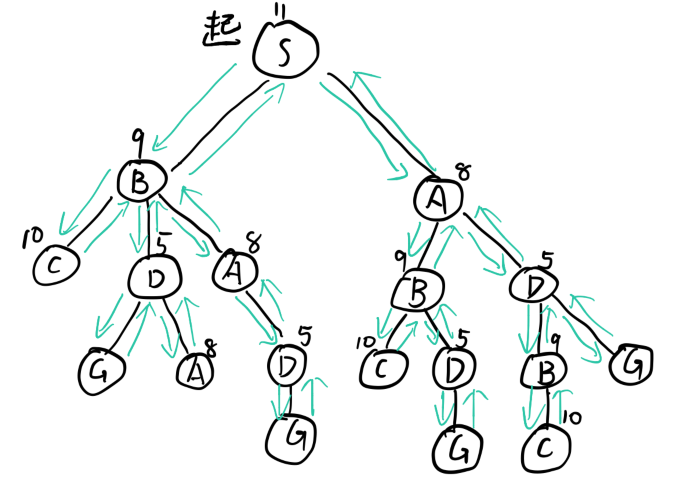
(b).广度优先

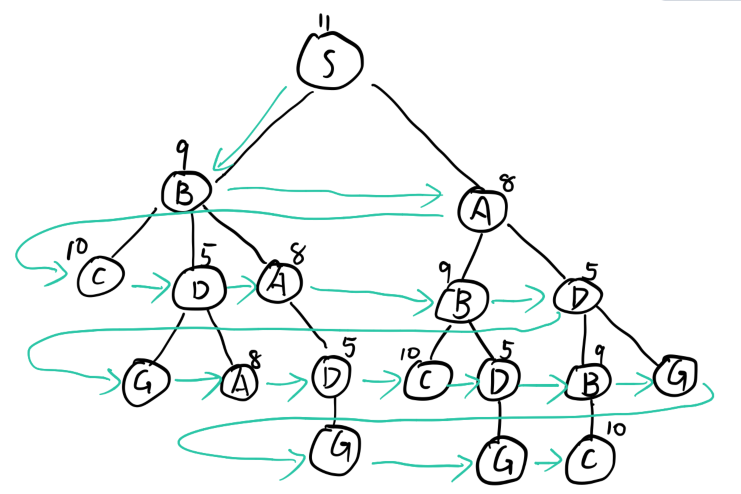
©.爬山法

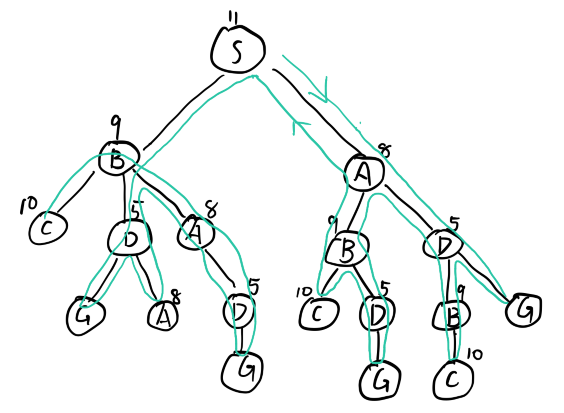
(d).最佳优先

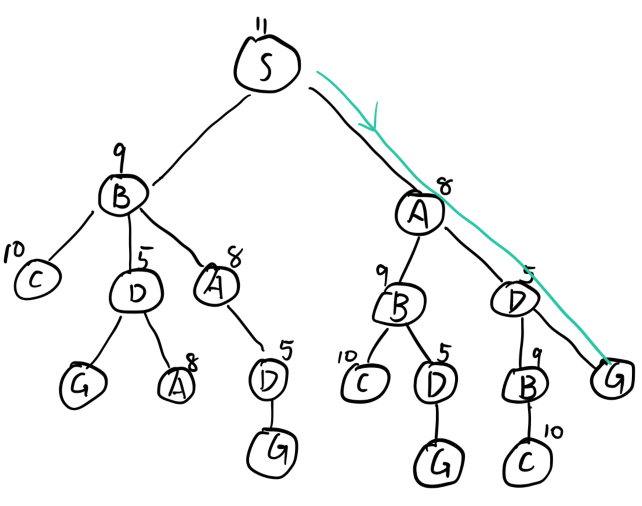
4. 搜索树代价计算

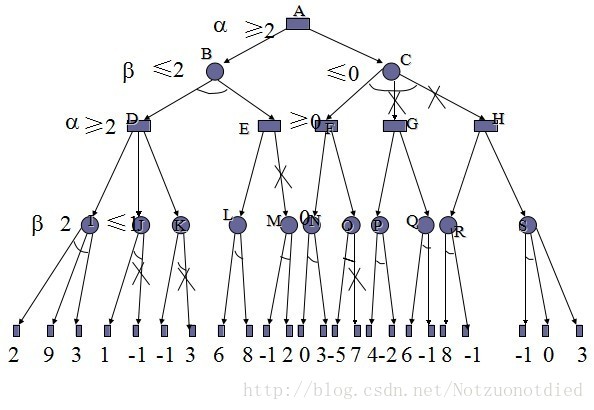
4. 图二是一棵部分展开的搜索树，其中树的边记录了对应的单步代价，叶子节点标注了到达目标结点的启发式函数的代价值，假定当前状态位于结点A：

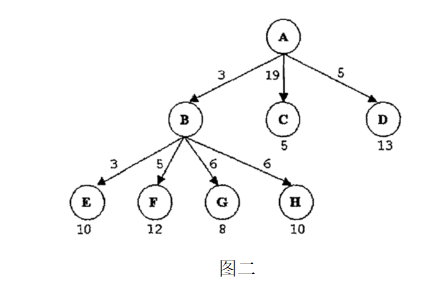
(a) 用下列的搜索方法来计算下一步需要展开的叶子节点，，
注意必须要有完整的计算过程，同时必须对扩展该叶子节点之前的节点顺序进行记录：

1. 贪婪最佳优先搜索
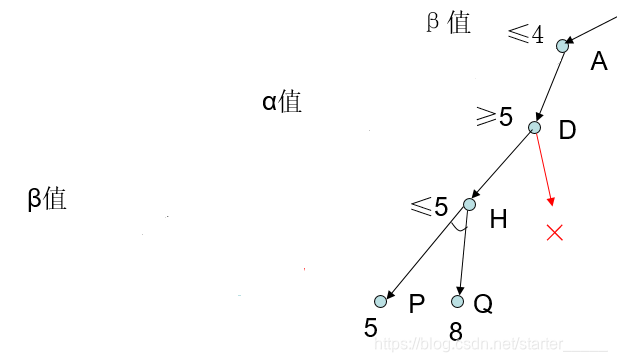
   首先，贪婪最佳优先算法是试图扩展离目标最近的节点，它只用到启发信息，也就是f(n)=h(n)；即使用启发函数，从状态n到目标的最短路径的估计耗散值h(n)作为从起点经过n到目标的最短路径估计耗散值f(n)；这里如果 h(B) >5 ，那么结点 c 距离目标结点最近，距离为 5 ，所以贪婪最佳优先算法先扩展 c 结点；如果h(B)<5，那么结点 B 距离目标结点最近，优先扩展 B 结点；
2. 一致代价搜索 （GBS）
   
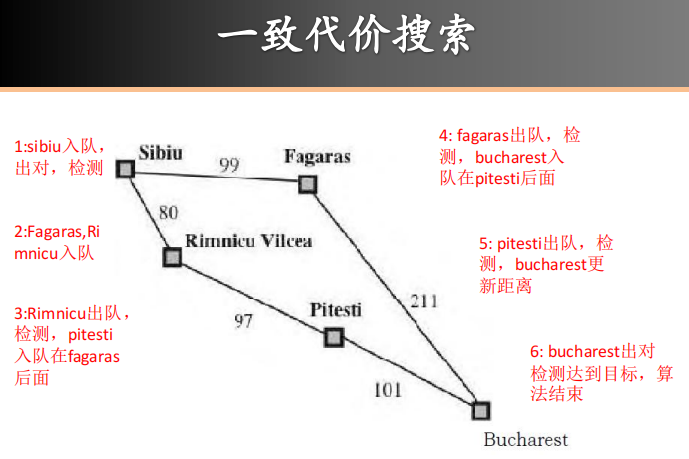
   —致性代价搜索扩展的是路径消耗最小的结点。所以一致代价搜索扩展的结点顺序为：BDEFGHC
3. A树搜索
   A搜索对节点的评估结合了g(n)，即到达此节点已经花费的代价，和h(n)，故f(n)=g(n)+h(n)，即经过节点n的最小代价；
   如果 h(B)>15，因为 5+13 < 3+h(B) <19+5，所以首先访问D；如果 h(B)<15，因为 3+h(B) < 5+13 <19+5，所以首先访问 B，然后再访问 E G D H F C；
   
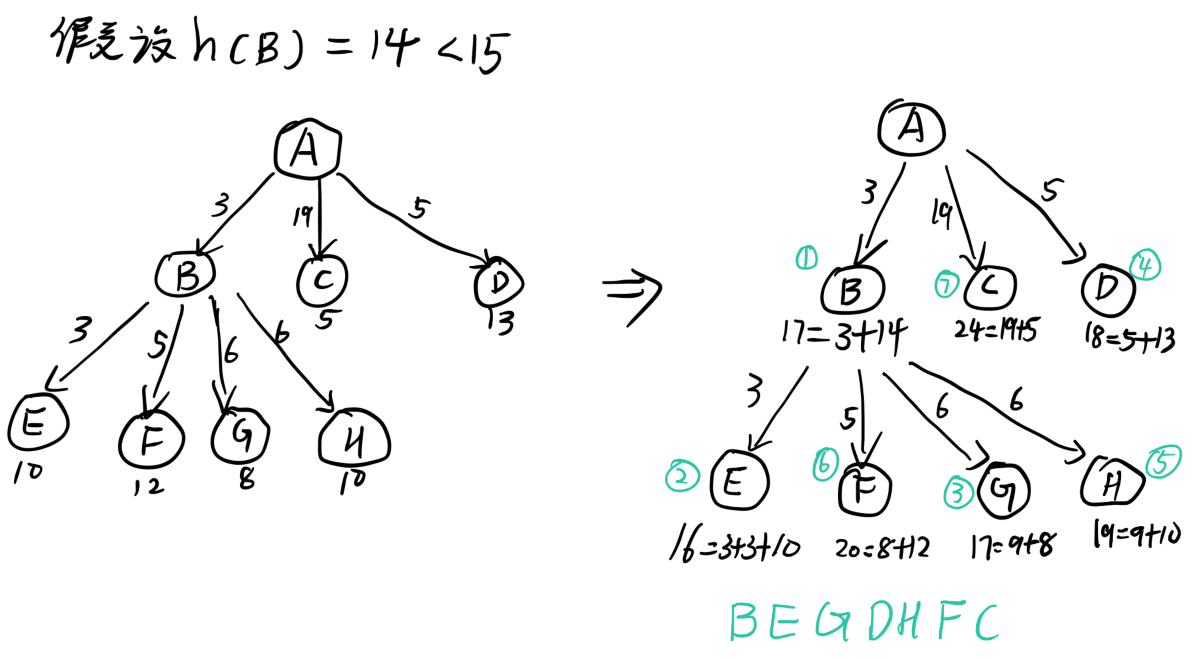
   https://blog.csdn.net/CCCrunner/article/details/102851569

(b) 讨论以上三种算法的完备性和最优性

• 贪婪最佳有限所搜算法试图扩展离目标距离最近的节点，因为这样符合贪婪的本质，能够很快找到解，它是不完备的，容易陷入死胡同或者死循环，类似DFS；
• 一致代价搜索算法按照结点的最优路径顺序扩展节点，这是对任何单步代价函数都是最优的算法，它不再扩展深度最浅的结点，它是完备的，类似BFS；
• A*树搜索是完备的，且对于给定的一致的启发函数都是效率最优的；

5. 博弈树

5. 博弈树问题
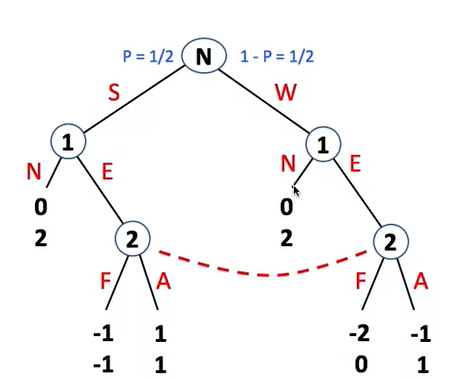
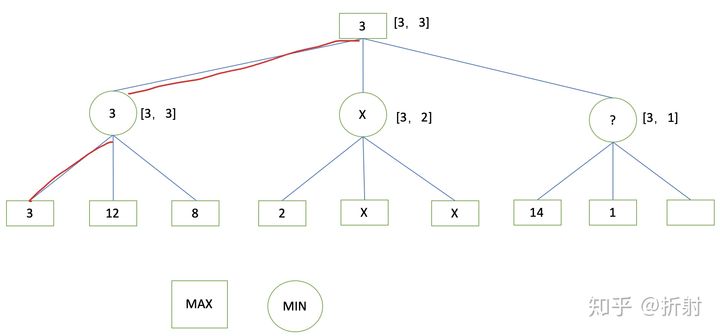
以下是一个博弈树轮到max选手行棋，叶子结点下的数字代表着当前状态的分值(相对于max选手)。

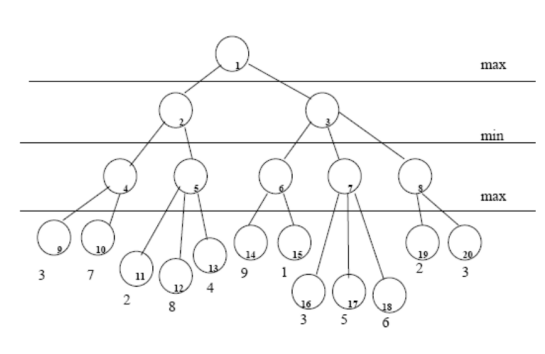
a)如果max选择走结点3且两个玩家正确游戏，那么该博弈树输出的分值是什么？

  当 max 选择走结点3时，min只有结点 6、7、8的选择，叶子结点表示 max 的赢面，如果 min 走结点7，那么 max 的赢面为3、5、6，这个赢面大于 min 走结点8后max的赢面 ，为了降低 max 赢的概率，min 一定不会走结点7；现在只剩结点6和8了，如果 min 走结点6，会面临让 max 赢面为9的可能，综合考虑：9*50%+1*50% > 2*50%+3*50%所以节点6使得 max 平均赢面为5，而结点8使得 max 平均赢面为2.5，所以 min 权衡之下，一定会走结点8，而 max 则会选择结点20，该博弈树输出值为3；

b)分析使用剪枝时(从左到右遍历)该树被裁剪的部分。

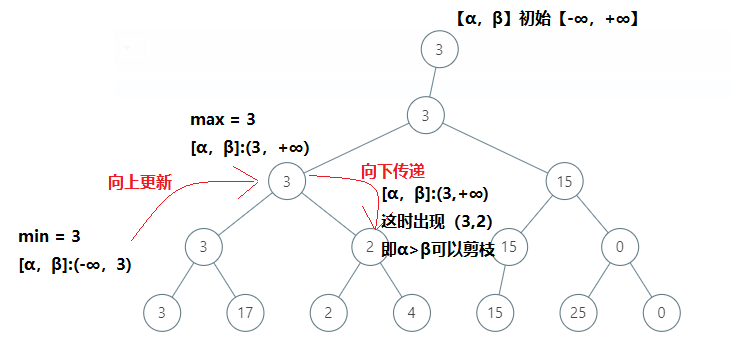
参考文章：
详解Minimax算法与α-β剪枝
https://www.bilibili.com/video/BV1o54y1e7gP?from=search&seid=2162585600183505084


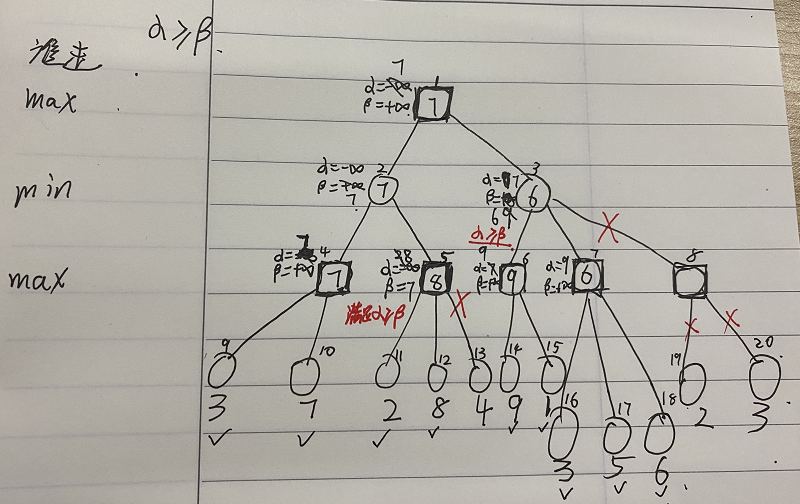
裁剪结点 13、8、19、20；

6. 四皇后问题

6. 考虑棋盘上的四皇后问题，最左边的一列为第一列,最上面的一行为第一行, Qi表示皇后在第i行所在的列数。假定皇后摆放的顺序为Q1,Q2,Q3,Q4, 且在每一行上按照从第一列到第四列的顺序摆放皇后，请运用回溯搜索算法结合前向检测来解决四皇后问题。

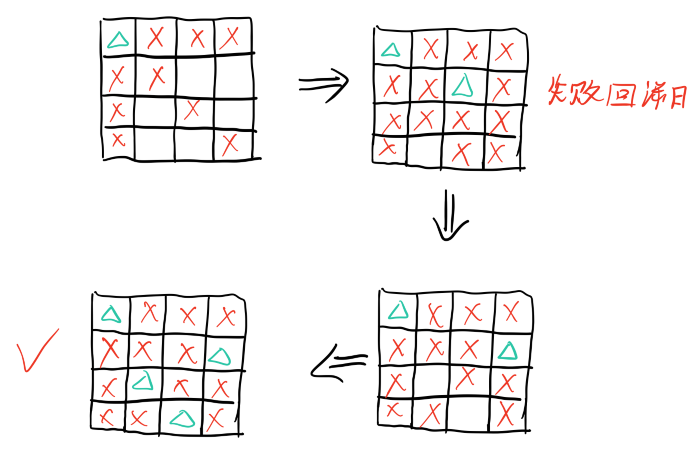
如果皇后摆放的顺序依旧为Q1,Q2,Q3,Q4,但不要求在每一行上从第一列到第四列摆放皇后，能够找出一种摆放策略来避免回溯失败？
对于皇后较少的n皇后问题，可以直观的比较互斥对的对数来决定放置位置：

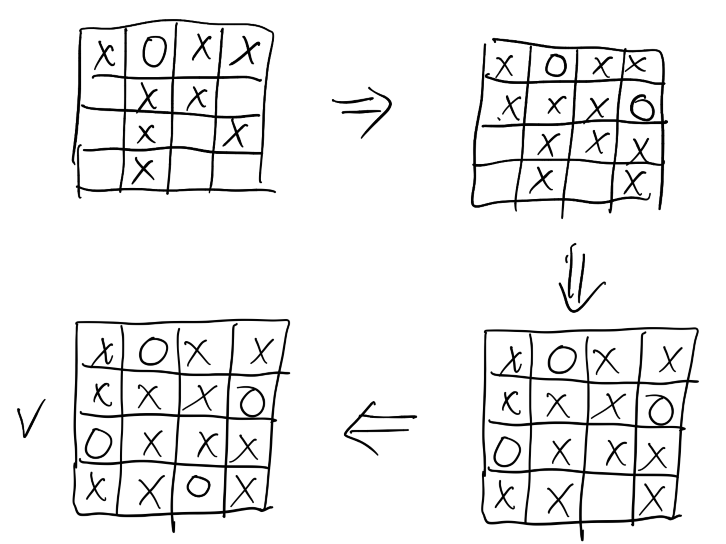
  如果第一个皇后放置在(1,1)位置，那么剩余可放置位置(图中空白位置，如(2.3).(2.,4),(3,2).(3,4),(4,2).(4,3))之间的互斥对数有8对。
  如果第一个皇后放置在(1,2)位置，那么剩余可放置位置(图中空白位置，如(2.4).(3,1),(3,3),(4,1),.(4,3),(4,4))之间的互斥对数有5对。
  后者互斥对数更少，表示放置皇后后发生冲突的可能性更小，所以优先将第一个皇后放在(1,2)位置；

7. 一阶逻辑表达式

7. 将下列语句转成一阶逻辑表达式。注意：仅限于使用如下谓词IsNew(x)，IsOld(x),IsBlue(x),IsBorrowed(x,y,z),Mother(x,y),Marriageable(x),Possess(x,y)
（1）所有旧的(old)东西都不是新的(new)；
∀x isOld(x) -> ¬ isNew(x)
（2）蓝色的(blue)东西是从某人的妈妈(mother)那里借来的(borrowed)；
∃x ∃m ∃n ∃y( isBlue(x) -> (Mother(m,n) ∧ borrowed(x, y,n)) )
（3）一个人必须要同时拥有一些旧的东西，一些新的东西，一些借来的东西，一些蓝色的东西才可以结婚(marriageable)；

∀x ∃m ∃n ∃y ∃z ∃b (Possess(x, (isOld(m)) ∧ Possess(x, isNew(n) ) ∧ Possess(x, isBlue(y)) ∧ Possess(x, isBorrowed(z,x,b))) -> Marriageable(x) )

8. CNF范式

8.将下列一阶逻辑语句转换为CNF范式
_{(x){P(x)→{(y)[P(y)→P(f(x，y))]∧}(y)[Q(x，y)→P(y)]}}
1）消除蕴含词 （p->q <=> ¬p∨q ）
得到：¬(x){¬P(x)∨{(∀y)[¬P(y)∨P(f(x，y))]∧~(∀y)[¬Q(x，y)∨P(y)]}}
2）否定词内移
得到：(∃x){P(x)∧{(∃y)[P(y)∧¬P(f(x，y))]∨(∀y)[¬Q(x，y)∨P(y)]}}
3）变量标准化：相同变量需变名
得到：(∃x){P(x)∧{(∃y)[P(y)∧¬P(f(x，y))]∨(∀z)[¬Q(x，z)∨P(z)]}}
4）skolem 化消除∃量词（∃y <=> g(x)）
得到：(g(z)){P(g(z))∧{(h(z))[P(h(z))∧¬P(f(g(z)，h(z)))]∨(∀z)[¬Q(g(z)，z)∨P(z)]}}
5）删除全称量词
得到：(g(z)){P(g(z))∧{(h(z))[P(h(z))∧¬P(f(g(z)，h(z)))]∨[¬Q(g(z)，z)∨P(z)]}}
6）将∧分配到∨中
得到：{(g(z))∧P(g(z))}∧{(g(z))∧(h(z))∧P(h(z))}∧{(g(z))∧(h(z))∧¬P(f(g(z)，h(z)))}∧{(g(z))∨¬Q(g(z)，z)}∧{(g(z))∨P(z)}

7） 把这个CNF变成5个子句：

• (g(z))∧P(g(z))
• (g(z))∧(h(z))∧P(h(z))
• (g(z))∧(h(z))∧¬P(f(g(z)，h(z)))
• (g(z))∨¬Q(g(z)，z)
• (g(z))∨P(z)