即使满腹经纶，但没有好的口才来授课，也会让学生听得昏昏欲睡、不知所云呢！即使满腔热血，没有好的口才来凝聚共识，也会让这份理想温暖黯淡无光。但是，好的说话之道，也要有一颗赤诚的心、诚恳的情来润饰，否则，很难做到说好话、做好事、做好人的成果！——《爱读书的孩子，不会变坏 (宋怡慧 著)》

0 引言

　　在智能过程中，搜索是必不可少的，是人工智能中的一个基本问题—— Nilsson。这是因为人工智能研究的主要是那些没有成熟方法可依的问题领域，需要一步步搜索求解。游戏中如何找到对自己有利的局面就属于这类问题。在游戏（人机博弈）程序中博弈树搜索算法是其核心的部分，它与估值及规则（走法）构成一个完整的系统。

1 α-β剪枝算法

1.1 基本思想

　　根据倒推值的计算方法，或中取大，与中取小，在扩展和计算过程中，能剪掉不必要的分枝，提高效率。

1.2 定义

　　α值：有或后继的节点，取当前子节点中的最大倒推值为其下界，称为α值。节点倒推值>=α；
　　β值：有与后继的节点，取当前子节点中的最小倒推值为其上界，称为β值。节点倒推值<=β；

1.3 α-β 剪枝

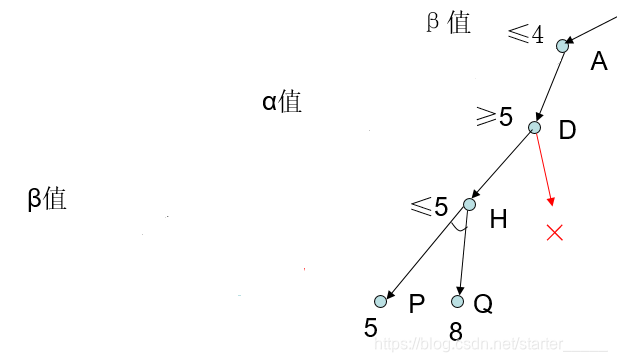
　　（1）β剪枝：节点x的α值不能降低其父节点的β值，x以下的分支可停止搜索，且x的倒推值为α；
　　（2）α 剪枝：节点x的β值不能升高其父节点的α值，x以下的分支可停止搜索，且x的倒推值为β；

1.4 例题图

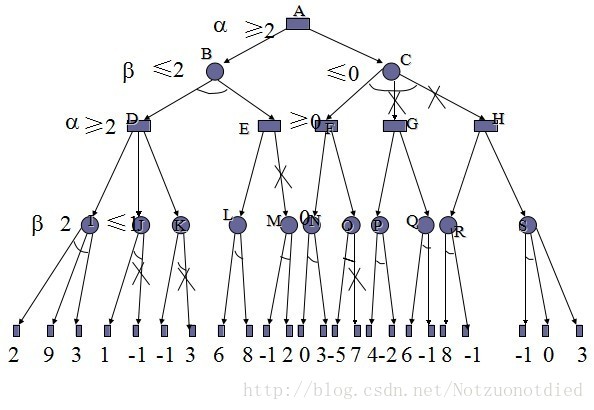
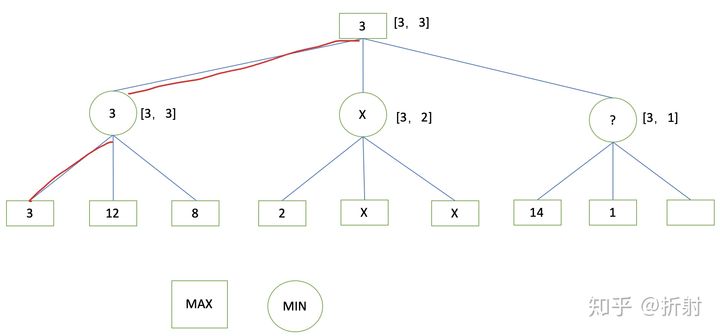
　　先做个说明：有画弧线的是与，取较小值，没有的是或，去最大值。
　　第一步：2、9、3做比较，取最小值2，I点确定为2。
　　第二步：J点的1和I点2大小进行比较，如果1是J点的最小值，由于J的父节点是取较大值，1<2，无法升高D的值，所以J点的-1可以点可停止搜索，我们划掉该值。
　　第三步：I点2接着与K点的左值-1进行比较，如果-1是最小值，由于K的父节点取较大值，-1<2，无法升高D的取值，所以K点的右值可以停止搜索。
　　第四步：D的值可以确定为2。
　　第五步：L点的作用值进行比较，取较小值6，D值与L值相比较，由于E去较大值，假设L就是最大值，E=6，二B点取得是D和E的较小。值，2<6，E的结果值无法降低B的取值，所以E的右枝可以截掉。
　　第六步：B的值可以确定为2。
　　第七步：N的左右值进行比较，取0,N点在和O点的左值-5进行比较，假设-5是最小值，0>-5,O点的取值无法升高父节点F的值，所以可以停止搜索O点的右枝。
　　第八步：F确定为0。
　　第九步：F点假设是C的最小值，它和B点的值比较，2>0,也就是说C点的取值无法升高A点的取值，所以G和H都停止搜索。

第十步：A点取2.

2 改进α - β剪枝算法

• Alpha-Beta剪枝(Alpha Beta Pruning)

2.1 窗口原则(Window Principle)

　　在α - β剪枝过程中，初始的的搜索窗口往往是从- ∞（即初始的α值）到+ ∞（初始的β值），在搜索进行中再不断缩小窗口，加大剪枝效果，这种估计是可靠的，但却不是高效的。如果我们一开始就使用一个较小的窗口，那么我们就有可能提高剪枝效率，这就是窗口原则。
　　使用窗口原则的算法有: Falphabeta 算法，即Failsoft-alphabeta算法; 渴望搜索（Aspiration Search）; 极小窗口搜索（Minimal Window Search/PVS）

2.2 置换表(Transpotion Table)

　　置换表基本思想: 在搜索进行中，用一张表把搜索过的节点结果（包括搜索深度，估值类型: 准确还是上下边界）记录下来，在后继的搜索过程中，查看表中记录。如果搜索的节点已经有记录（子树的深度大于或者等于当前的新节点要求的搜索深度），它的信息就可以直接运用了，这样我们可以避免重复搜索很多子树。置换表是一种内存增强技术，以空间换时间。

2.3 历史启发（History Heuristic）

　　历史启发是为了迎合α-β剪枝搜索对节点排列顺序敏感的特点来提高剪枝效率的，即根据历史走法对当前搜索的节点集进行排序，从而优先搜索好的走法。

2.4 迭代深化（Iterative Deepening）

　　迭代深化是一个不断求精的过程，对博弈树进行多次遍历，并不断加深其深度，用于控制搜索的时间。
　　在实用中迭代深化和前面提到的算法结合使用具有很好的效果，如PVS算法，上几层迭代得到的最佳走法可以帮助下一层提高剪枝效率; 迭代过程中把前面局面的历史得分存入置换表，最佳走法存入历史启发表可以提高剪枝效率。

2.5 实验数据分析

　　各种增强策略都能提高α - β剪枝的效率，其中空窗口探测(PVS)从第五层开始平均需估计的节点数减少为一半，而效率提高一倍。单纯的迭代深化由于在迭代需要耗费时间，从效率上看提高不大。置换表在前三层没什么表现，这是因为置换表操作也要耗费时间，且当其命中率低时效果不佳，但层数较多命中率高时优势越来越明显。历史启发是这几种增强策略中最好的，在第五层效率就能提高十倍以上，越往后效果更好，这也证实了α-β剪枝对顺序的极度敏感。
　　MTD(f)算法在实验中的前几层稍优于PVS 算法，但它层数大于六时很不稳定且本身带置换表，因此在把各种增强策略融合时不如PVS 算法。融合各种增强策略的PVS 算法在第六层就比基本的α - β剪枝快两百多倍。

3 B* 算法

3.1 B* 算法的思想与要点

　　B* 算法是由Hans J. Berliner在1979年提出来的一个算法，毫无疑问B*算法是到目前为止最具有人类风格的棋手[6]。
　　Berliner在研究极小极大搜索树的时候，认为有两个问题是关键的。
　　第一个问题是：如何降低组合搜索的复杂性，即如何尽早地查出不合用的坏分支，并把它剪除。这一步涉及到了进一步改进Ａｌｐｈａ－Ｂｅｔａ剪枝。
　　第二个问题是：如何合理地确定搜索的深度限制，已解决他本人提出的所谓水平效应（见下小节）。为了做到这一点，应该对每个分枝的前景有一定的定量的展望，以便及早放弃前途不大的搜索方向。

3.1.1 水平效应

　　由于固定搜索深度而引起的问题称为“水平效应”。
　　负水平效应：
　　如果一个搜索程序前进到了某个深度的时候，自以为找到了一个比较有利的结局，但是它不知道，若再深入几步就可以看出，真正的结局原来是不利的。这种看不出危险的毛病称为负水平效应。
　　正水平效应：
　　如果一个搜索程序在极限深度处发现了一种不利的局面，于是决定放弃这个方向。但是它不知道，只要再搜索几步即可出现“柳暗花明又一村”的好形式，由于“眼光”太短浅而没有做“再坚持一下”的努力。这种情况称为正水平效应。

算法的思想与要点

　　每个节点用一个乐观估值和一个悲观估值来表示评价值。
　　两个估计值都动态可变，且估值出自同一方的立场，只是估计的棋局按层次交错更替。对对方棋局的乐观估计即是对本方棋局的悲观估计; 对对方棋局的悲观估计即是对本方棋局的乐观估计。因此，从下层节点向上层节点反馈信息时，悲观估计和乐观估计是交叉传递的。
　　B*树在展开过程中，只要子节点的估值有利于父节点估值的精化，即改动父节点的估计值，即使乐观估值和一个悲观估值相互靠近(当当前节点深度大于零时需回溯)，如果这种改动波及到父节点的估值，则根节点需考虑使用何种策略。
　　B*算法设立两种策略，证明最优( P R O V E B E S T ) 和排除其余(DISPROVEREST)。
　　算法从这点出发，用这两个界来证明哪个节点是最好的。当根节点的一个孩子的悲观值不比所有其它节点的乐观值差的时候，B* 算法就结束了。
　　算法的搜索控制就是尽可能快的得到终止条件。B* 算法的优点是找到一步好棋速度快，不限定搜索深度，不会“产生水平效应”（这是固定深度α-β剪枝算法的一个缺点），缺点是它对局面的乐观值和悲观值的估计依赖性太强，实现困难。

3.2 B* 算法伪代码

typedef struct statue
{qiju con; // qiju 为当前棋局内容(数组)int opt; // 棋局乐观估计值int pes; // 棋局悲观估计值unsigned par; // 父节点所在的地址unsigned eld;// 长子节点所在的地址unsigned young;幼子节点所在的地址
} STATUE;
sta = { cur-qiju, -ININITY, ININITY, 0, 0, 0 };
qiju BXin(STATUE sta)
{vector< STATUE > v;unsigned al = 1; // 第一可分配的位置unsigned depth = 0; // 当前搜索深度（层次）unsigned cur = 0; // 当前节点的地址STATUE st;v.push_back(sta);while(1){if(v[cur].eld == 0) // 当前节点未扩展过{int count = CreatePossibleMove();for（each possibly move m）{make move m // 产生 m 的子节点// 创建子节点的状态construct child’s STATUE st;v.push_back(st);}v[cur].eld = al; // 修改长子节点所在地址// 修改幼子节点所在的地址v[cur].young = al + Count - 1;al += count; // 修改第一可分配的位置}// 建立最佳节点和次佳节点
lab:best = next = pest = v[cur].eld;if(depth%2 == 0) //偶数层for(i = v[cur].eld; i <=v[cur].young; i++){if(v[best].opt < v[i].opt)best = i; // 修改极大乐观值节点位置if(v[next].opt < v[i]. opt t &&v[i].opt < v[best]. opt)next = i; // 修改次极大乐观值节点位置if(v[pest].pes < v[i]. pes)pest = i; // 修改极大悲观值节点位置}else// 为奇数层for(i = v[cur].eld; i <=v[cur].young; i++){if(v[best].pp.first > v[i].pp.first)best = i; // 修改极小乐观值节点位置if(v[next].opt>v[i].opt&&v[i].opt> v[best]. opt)next = i; // 修改次极小乐观值节点位置if(v[pest]. pes > v[i]. pes)pest = i; // 修改极小悲观值节点位置}int opt = v[best].opt;int pes = v[pest].pes;// 满足条件,则修改当前节点的估计值，并在深度大于零时进行回溯if( ((depth%2 == 0) && (opt < v[cur].pes || pes > v[cur].opt))|| ( (depth%2 == 1) && (opt >v[cur].pes || pes < v[cur].opt)) ){v[cur].pes = opt;v[cur].opt = pes;if(depth > 0){cur = v[cur].par;depth--;goto lab; //回溯}else// 有一枝的悲观值不小于其它枝的乐观值，则搜索结束。if(v[best].pes >= v[next].opt)return v[best].con;}if(depth == 0)// 决定下一步的策略{if(take provebest strategy) cur = best;else cur = next;}if(depth > 0) cur = best;depth++;}
}

3.3 实验说明

　　实验中用的策略为Berliner 原则：用一组候选分枝与最佳分枝做比较，如果各候选分枝实行信息反馈的深度是ti，最佳分枝实行信息反馈的深度是t，比较Σti2和t2,若前者小于后者，则采用DISPROVEREST策略，否则采用PROVEBEST策略，即优先搜索那些至今搜索深度比较浅的分枝。由于B* 算法对估值的依赖性很强，实验所用的估值效果实现算法速度很快（时间小于一秒），但走法只有搜索深度为三层α - β剪枝的水准，实用时有待进一步提高。

4 SSS*算法

• 状态空间搜索-(转)

5 结束语

　　以上讨论了博弈树搜索算法的两类算法，其中α - β剪枝算法比较成熟，是当前最常用的算法，在融合各种策略后具有很高的剪枝效率。如果能进一步改进数据结构和进行代码优化以及使用开局、残局库可以使程序具有很高的效率智能。B* 算法由于其复杂性，一般使用较少，国内研究的热情不高，有待进一步研究，包括如何对棋局进行估值，使用何种策略以及与在中国象棋、围棋等游戏中实现。

6 参考文献

[1]陆汝钤.《人工智能》[M].北京：科学出版社，1995.
[2]王小春．游戏编程（人机博弈）[M]．重庆：重庆大学出版社，2002.
[3][美]Nils J Nilsson．人工智能[M]．北京: 机械工业出版社,2000
[4]Knuth, D.E. and Moore, R.W. (1975). An Analysisof Alpha-Beta Pruning[J]. Artificial Intelligence,Vol. 6, No. 4:293-326.
[5]Berliner, H.J. (1979). The B*-tree search: Abest-first proof procedure[J]. Artificial Intelligence,Vol. 12, No. 1:23-40.