前言

产生本文的缘由

人工智能原理课程可选实验 “AlphaBeta剪枝算法求解博弈树最优选择”,
以及去年在数据结构导论没有看明白的博弈论.
记录自己的学习过程.

注:本文适合有一定基础的读者阅读.

以下是本篇文章正文内容

一、AlphaBeta剪枝是什么？

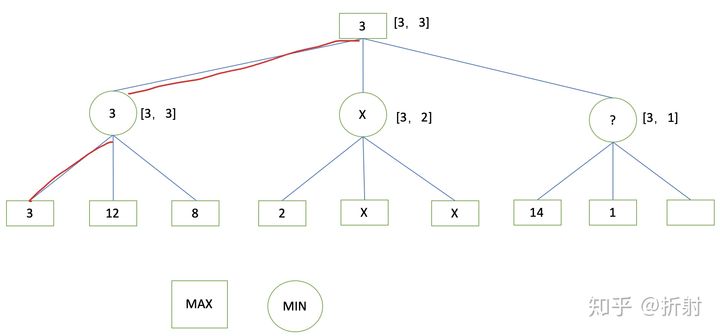
1.由来, 最大最小决策树

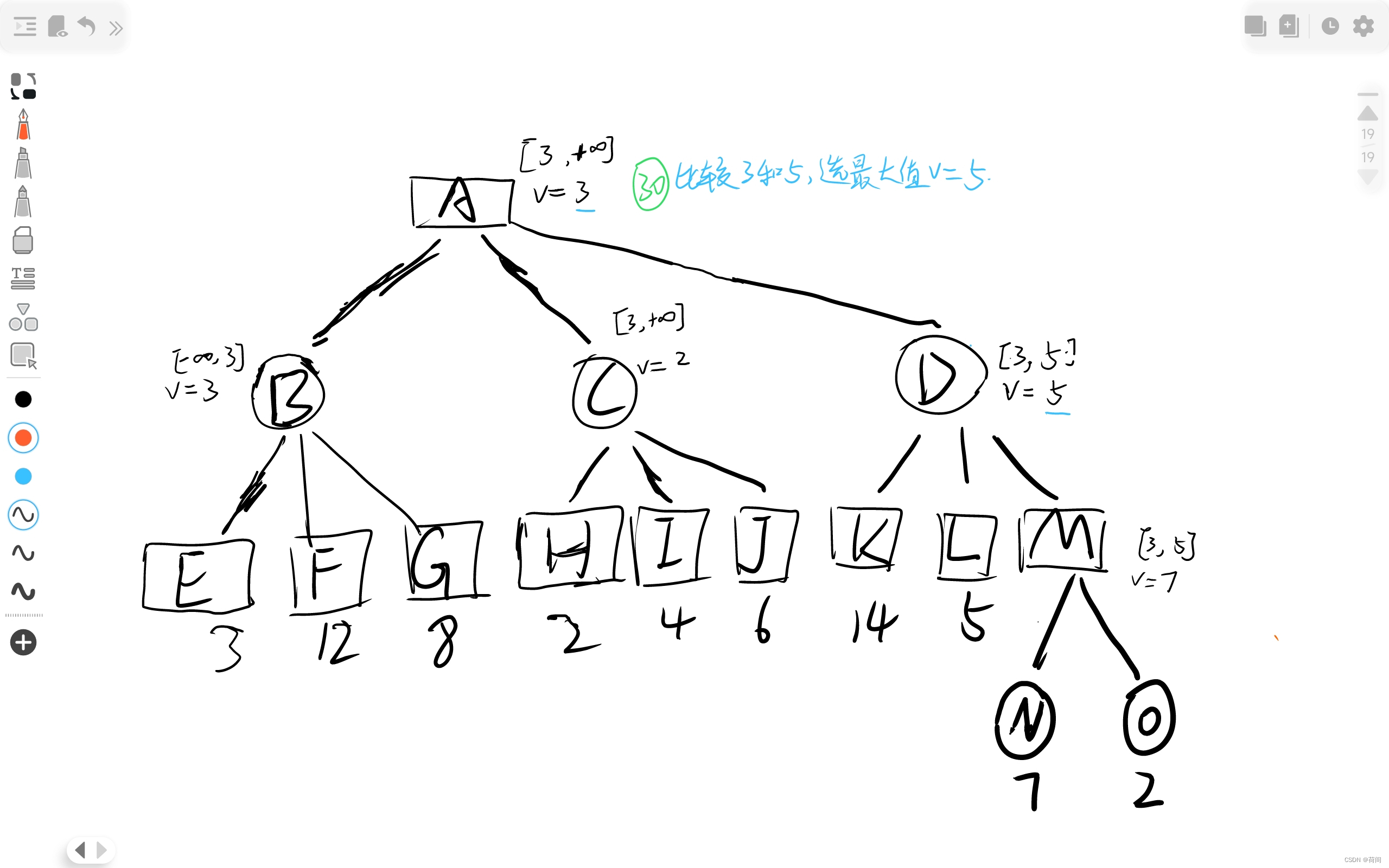
矩形一层的节点选择较大值
圆形一层的节点选择较小值
深度搜索比较节点值加上回溯即可.
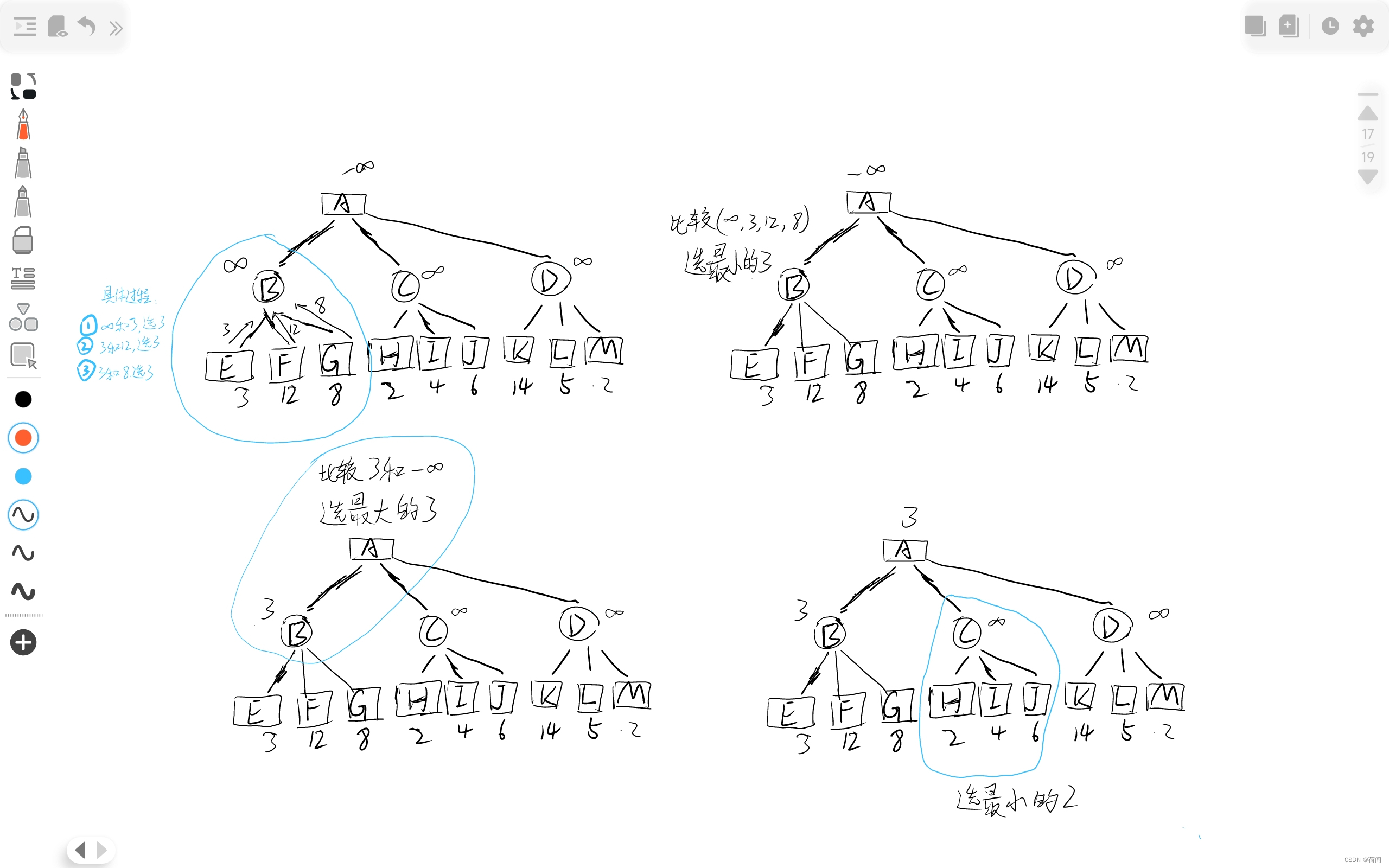
在这里插入图片描述

2.发展

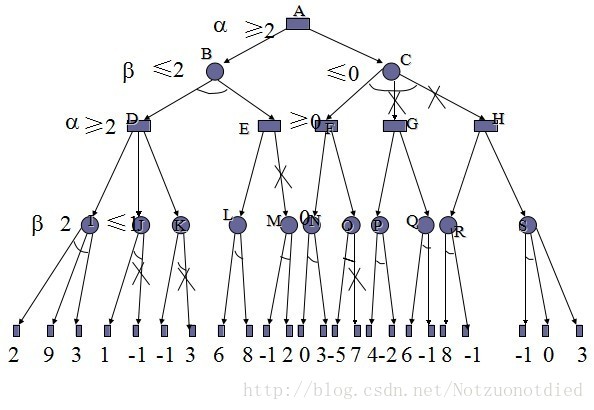
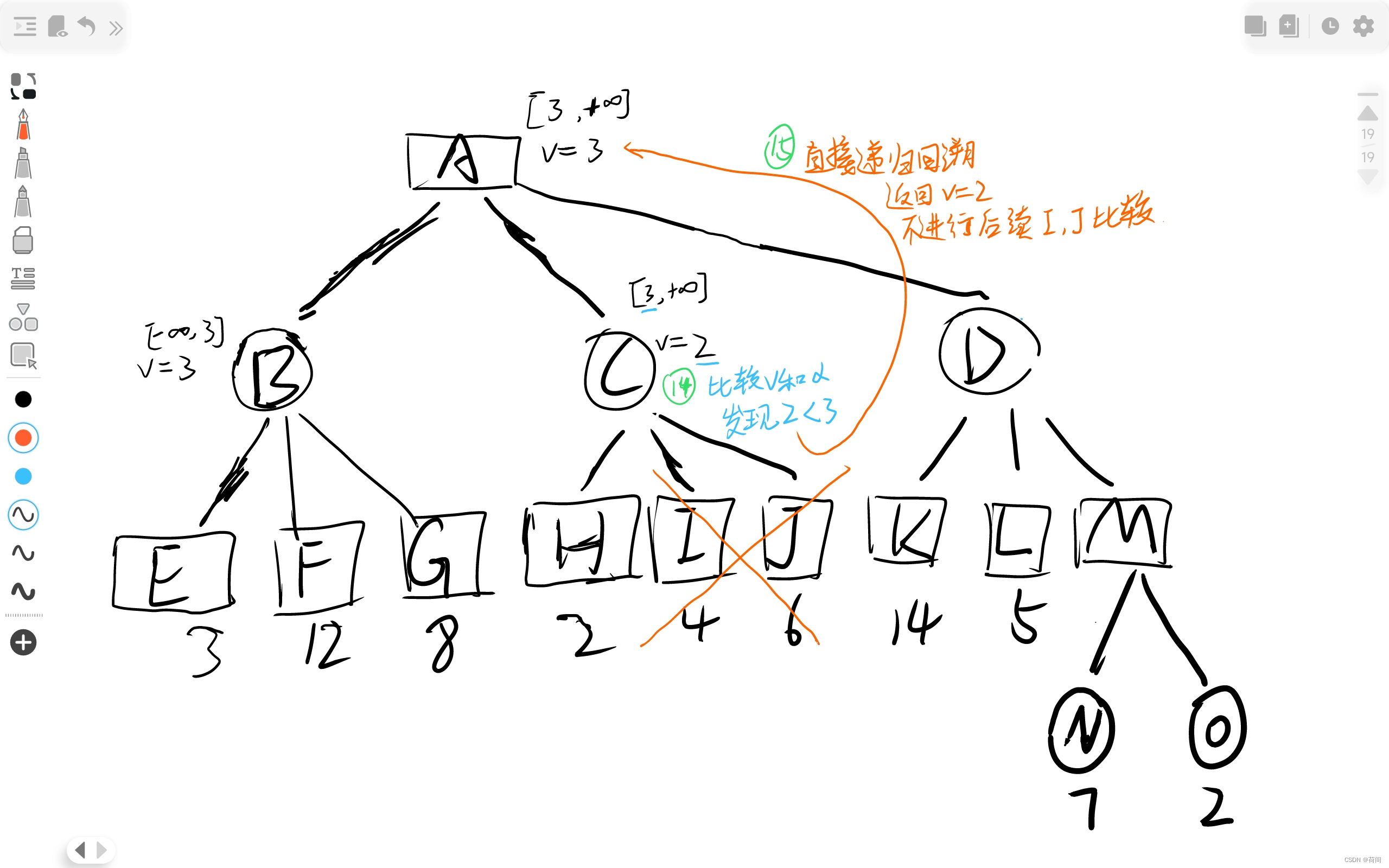
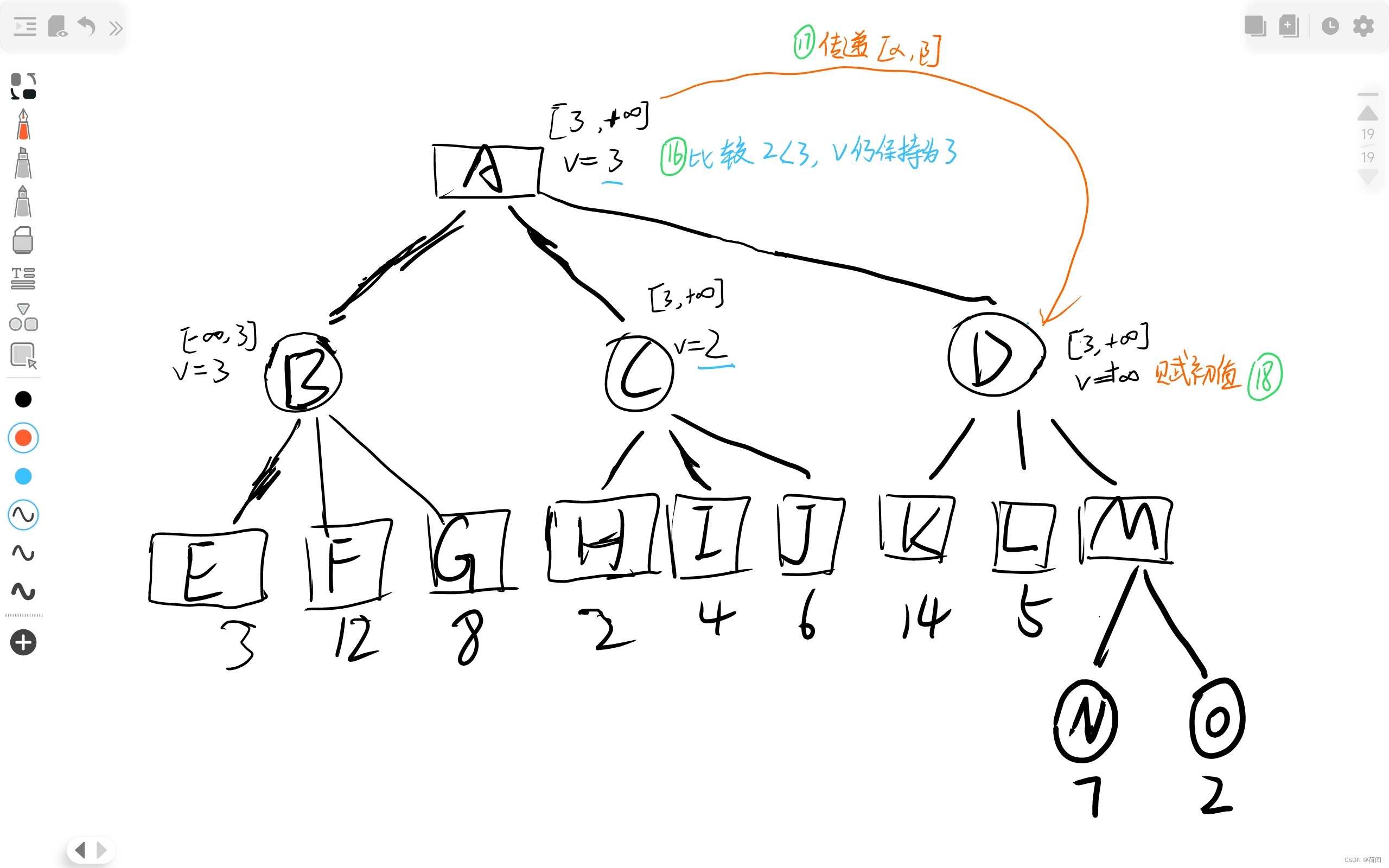
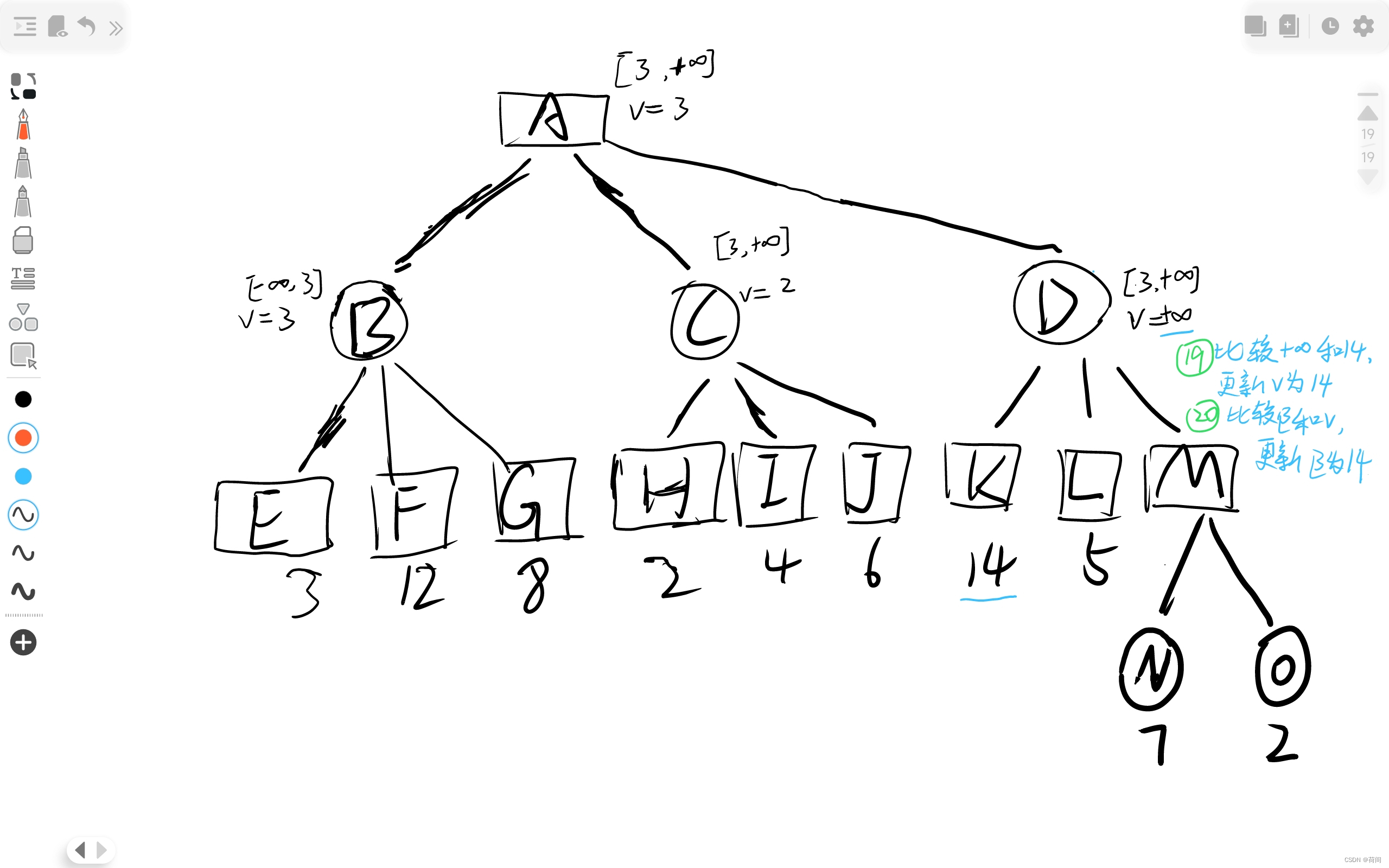
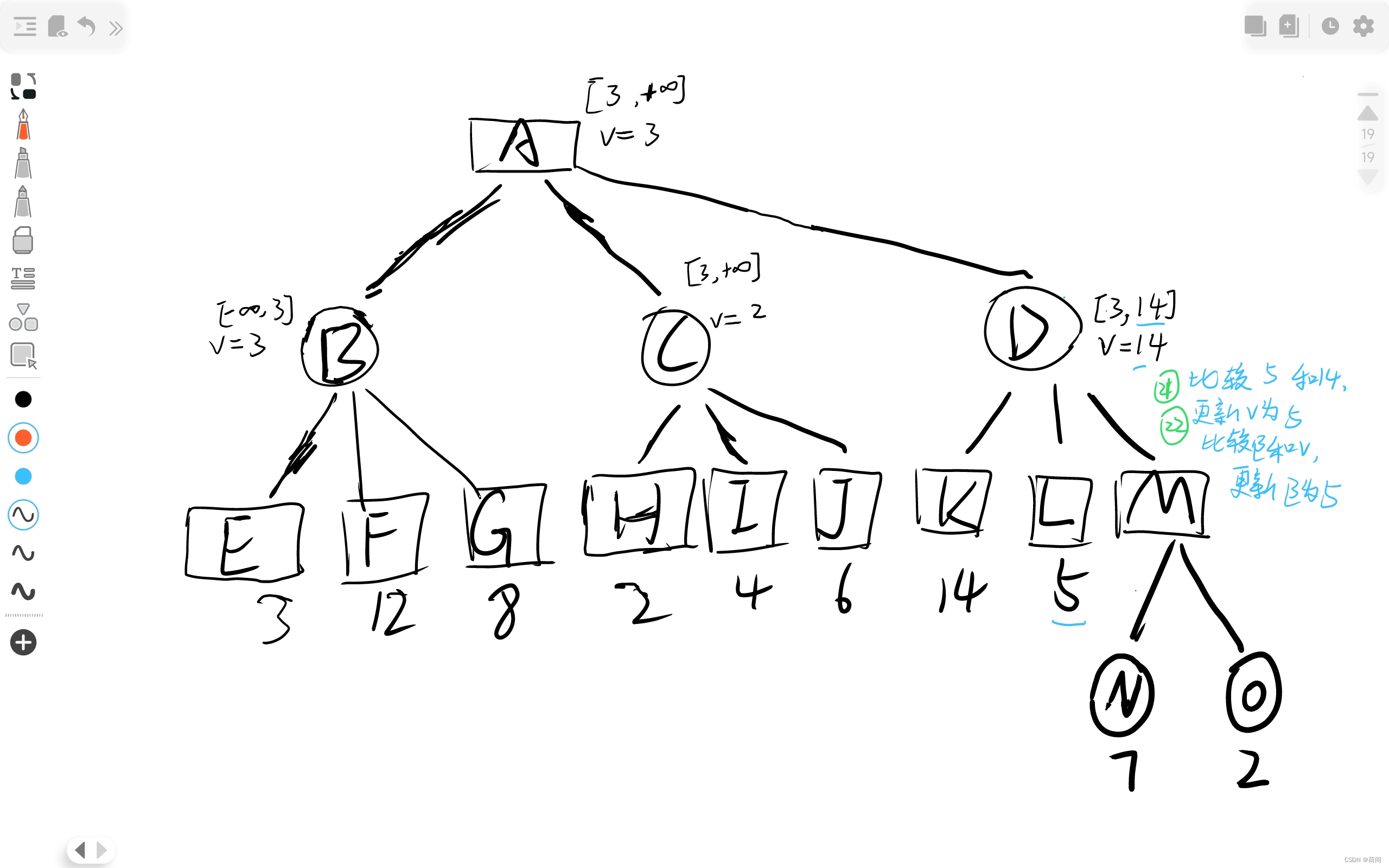
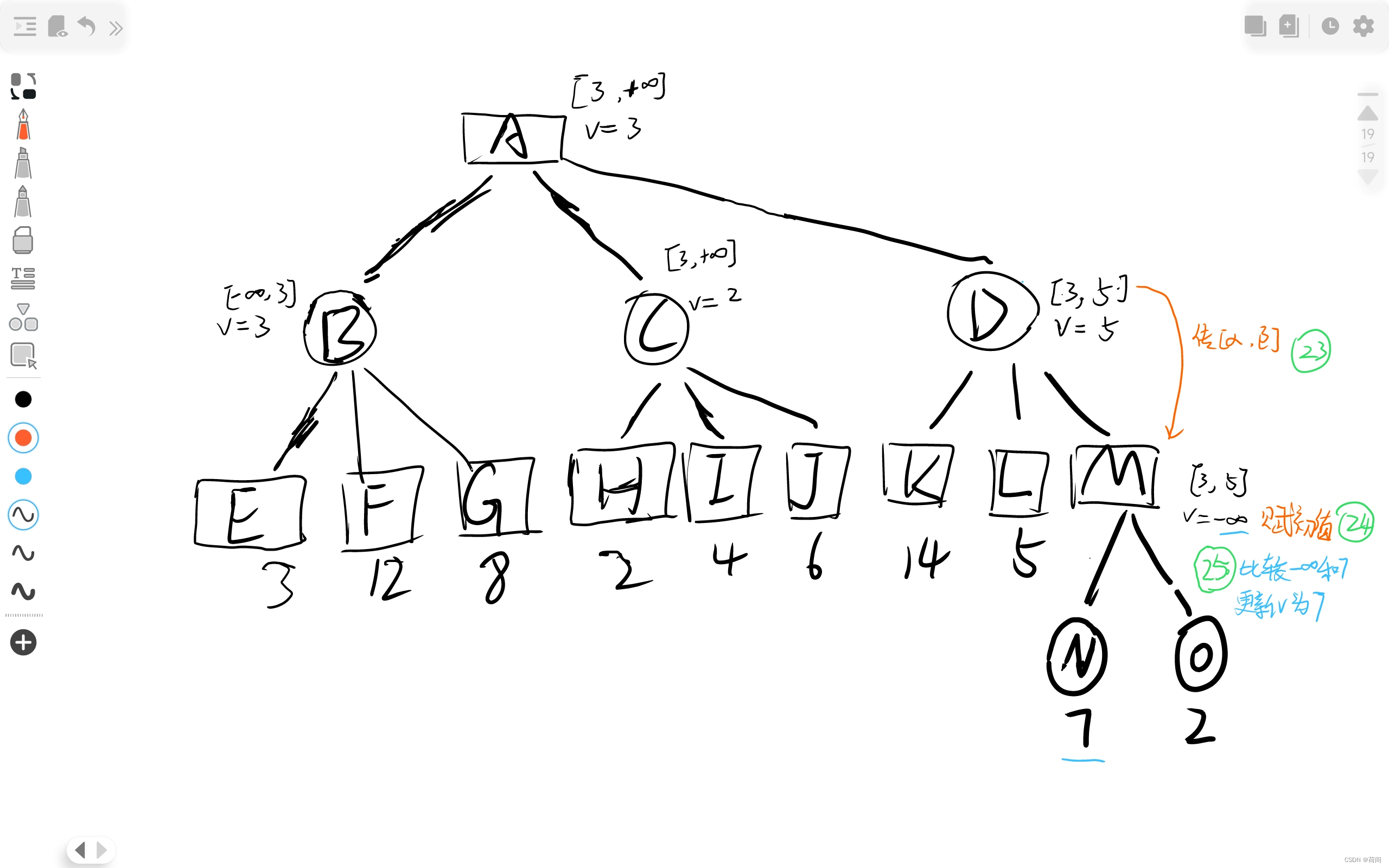
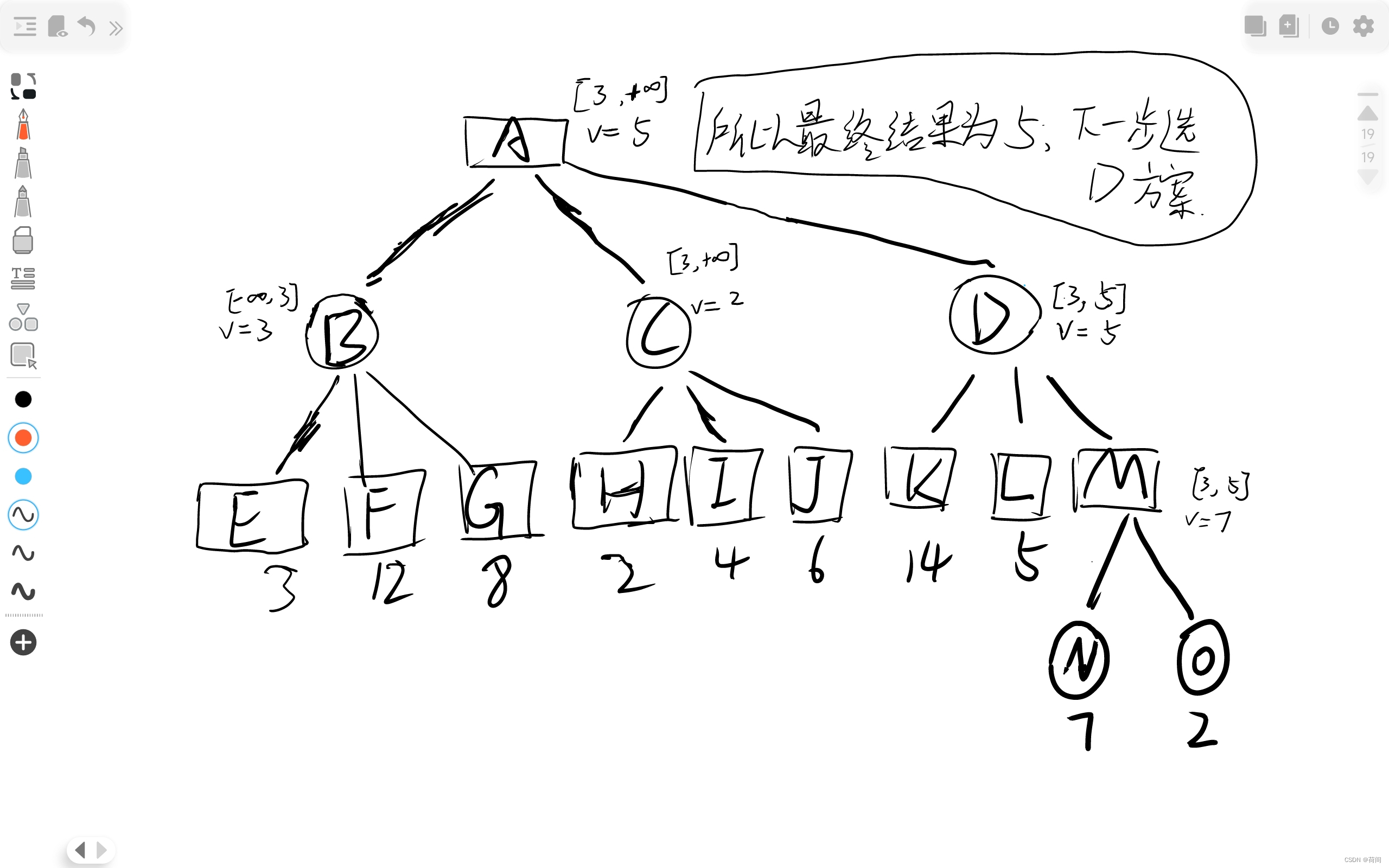
人们发现这些节点的比较过程很多是无意义的, 比如说对于上图的H节点
当C节点的正无穷大和H节点的2比较时, C节点值更新为2, 此时, 由于C是圆形一层的节点,
只能选择较小值.

那么C节点的取值只能小于等于2了

但是矩形节点A是在圆形节点B, C, D中选择一个最大的值

然而B节点的值已经为3 , 那么A不可能考虑C了

,所以对于C的子节点 H, I , 都没有必要继续进行访问并且比较更新C的节点值了

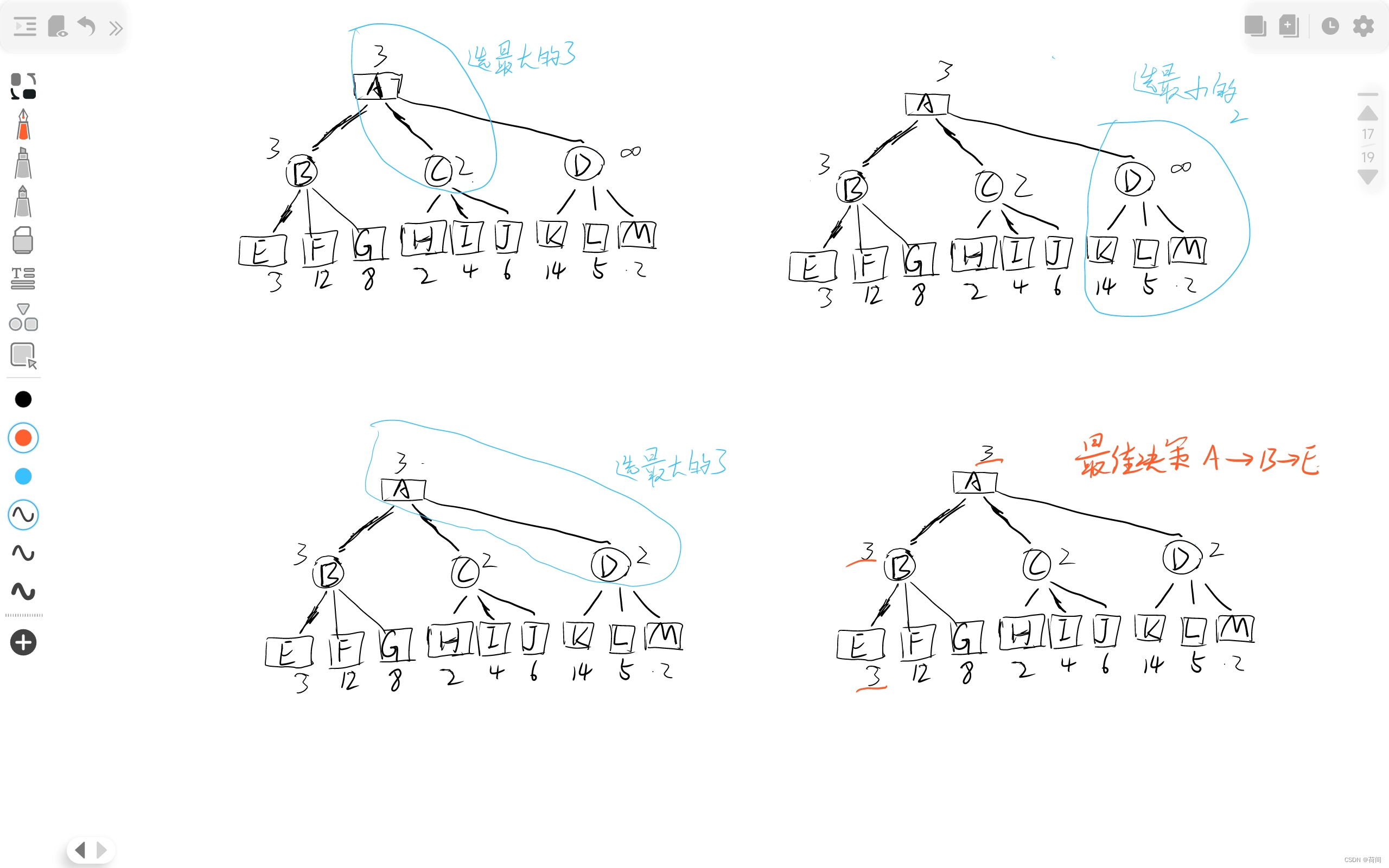
3. AlphaBeta剪枝

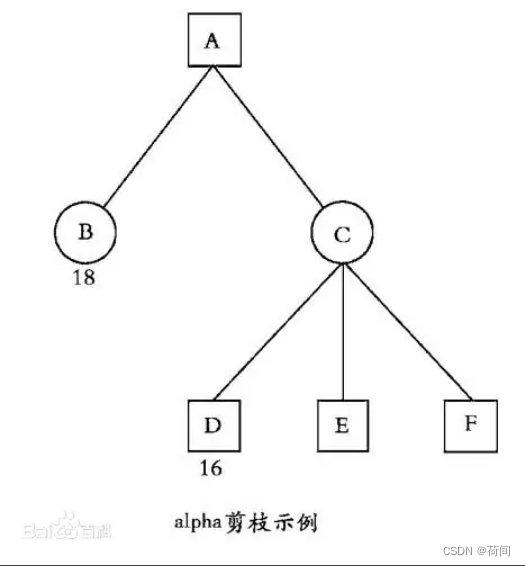
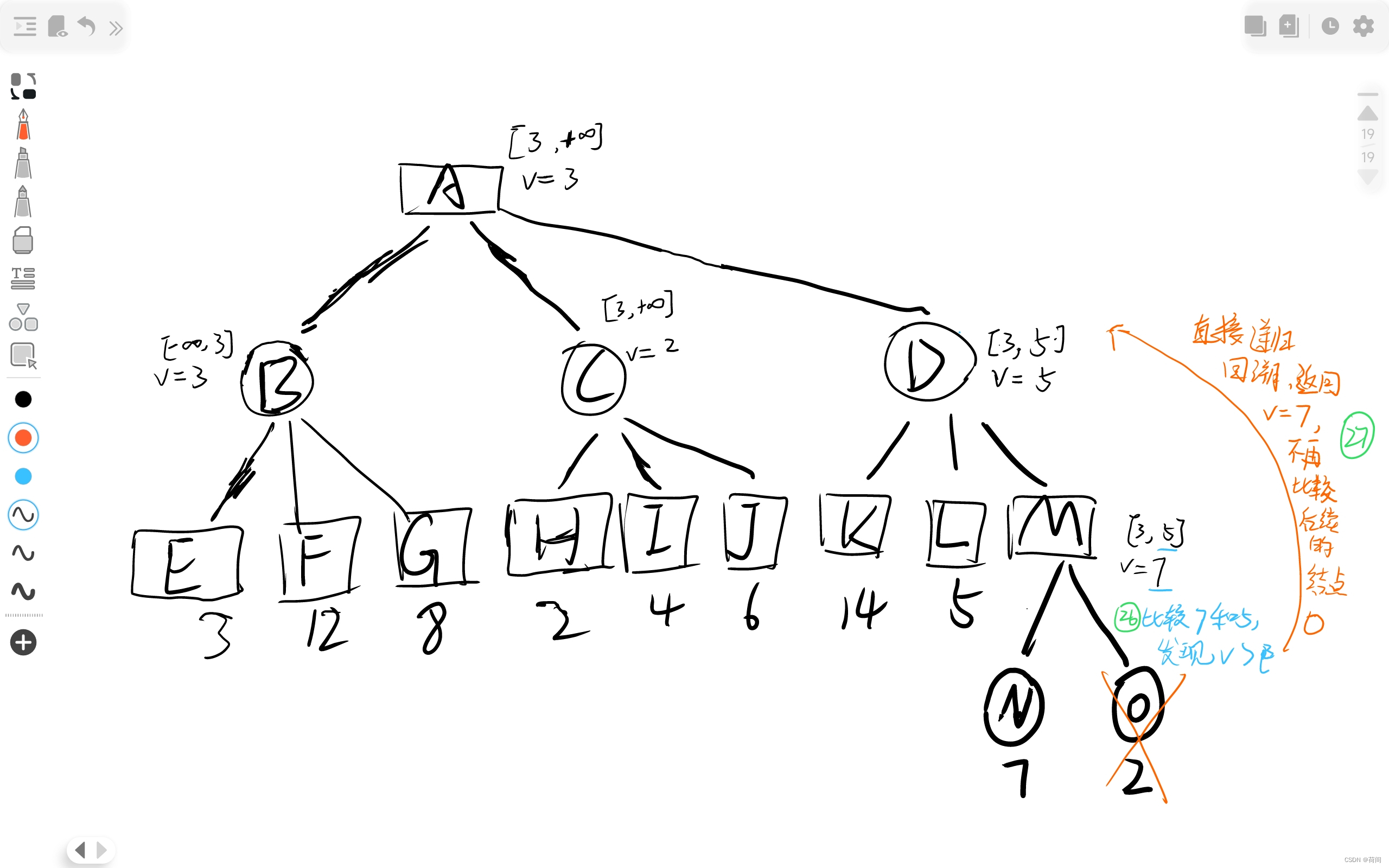
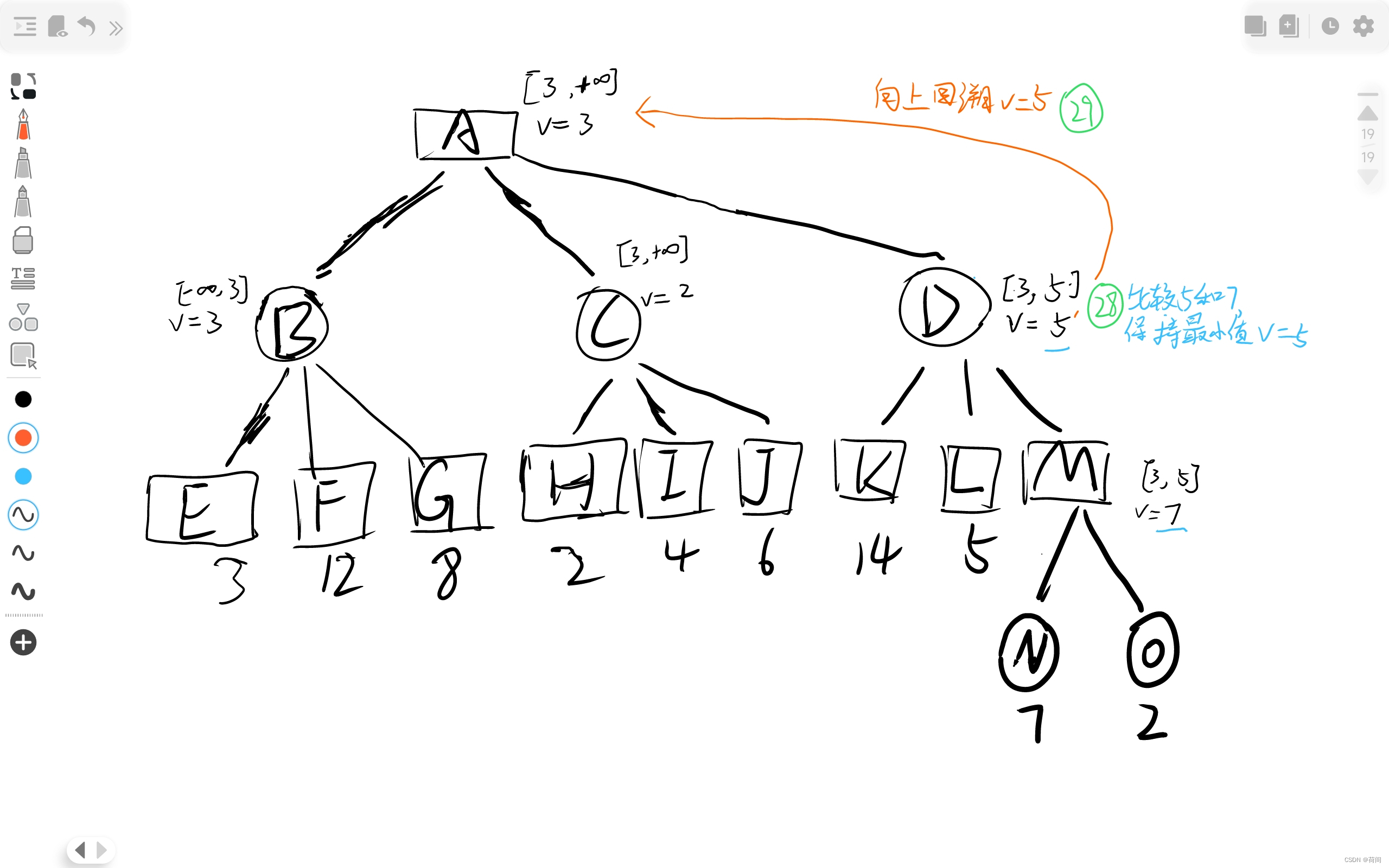
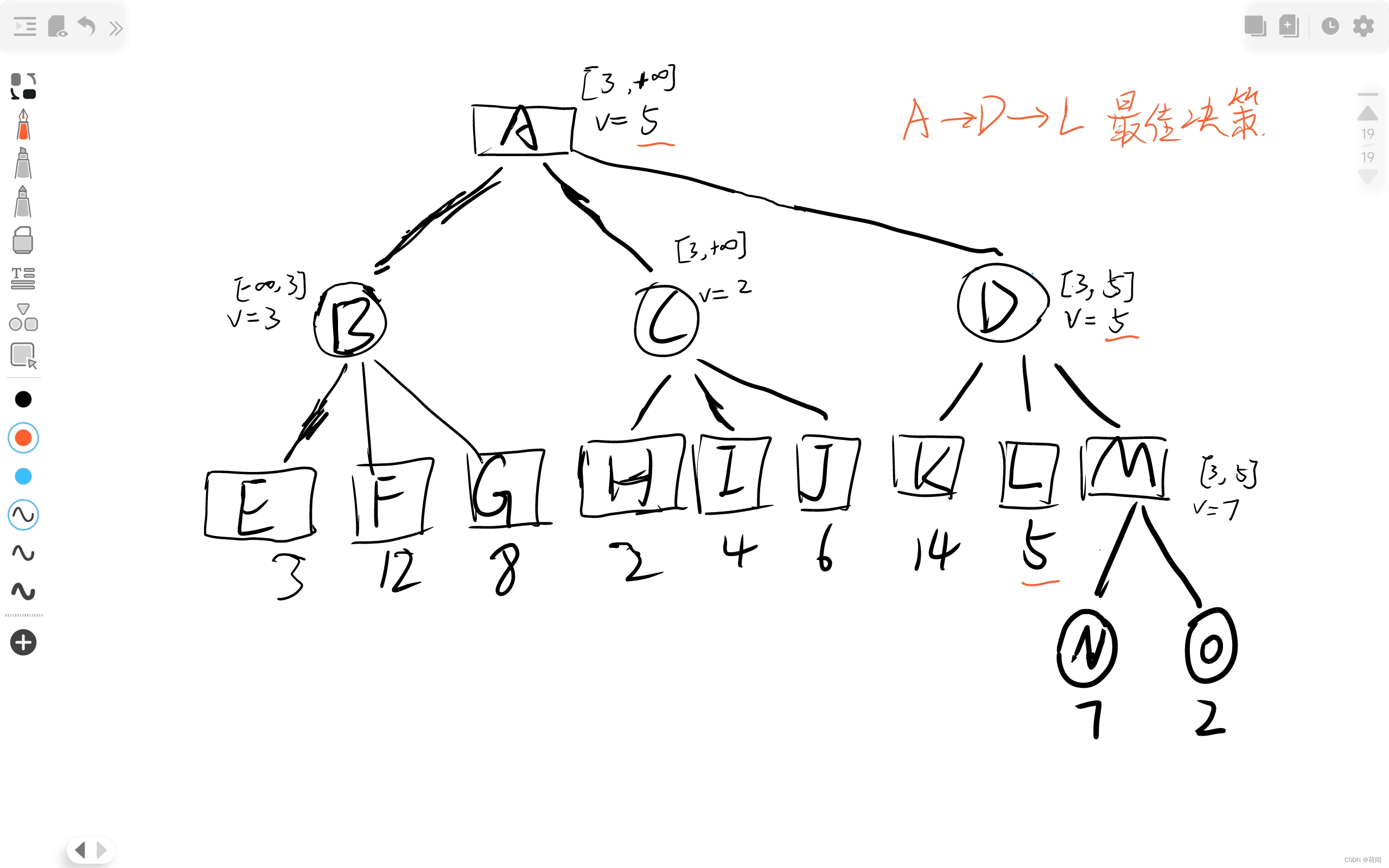
在这里插入图片描述

有图有真相 , 橙色画叉的就是剪枝的部分了, 根据该节点是矩形和圆形来判断是Alpha还是Beta剪枝 , 比如说C节点划掉了I 和 J , 而C节点是圆形的, 所以是Alpha剪枝.

其实更准确的定义是, 当时是因为v<=alpha 还是 v>=beta 剪枝来判断的, 比如说C节点进行剪枝的时候, v<=alpha

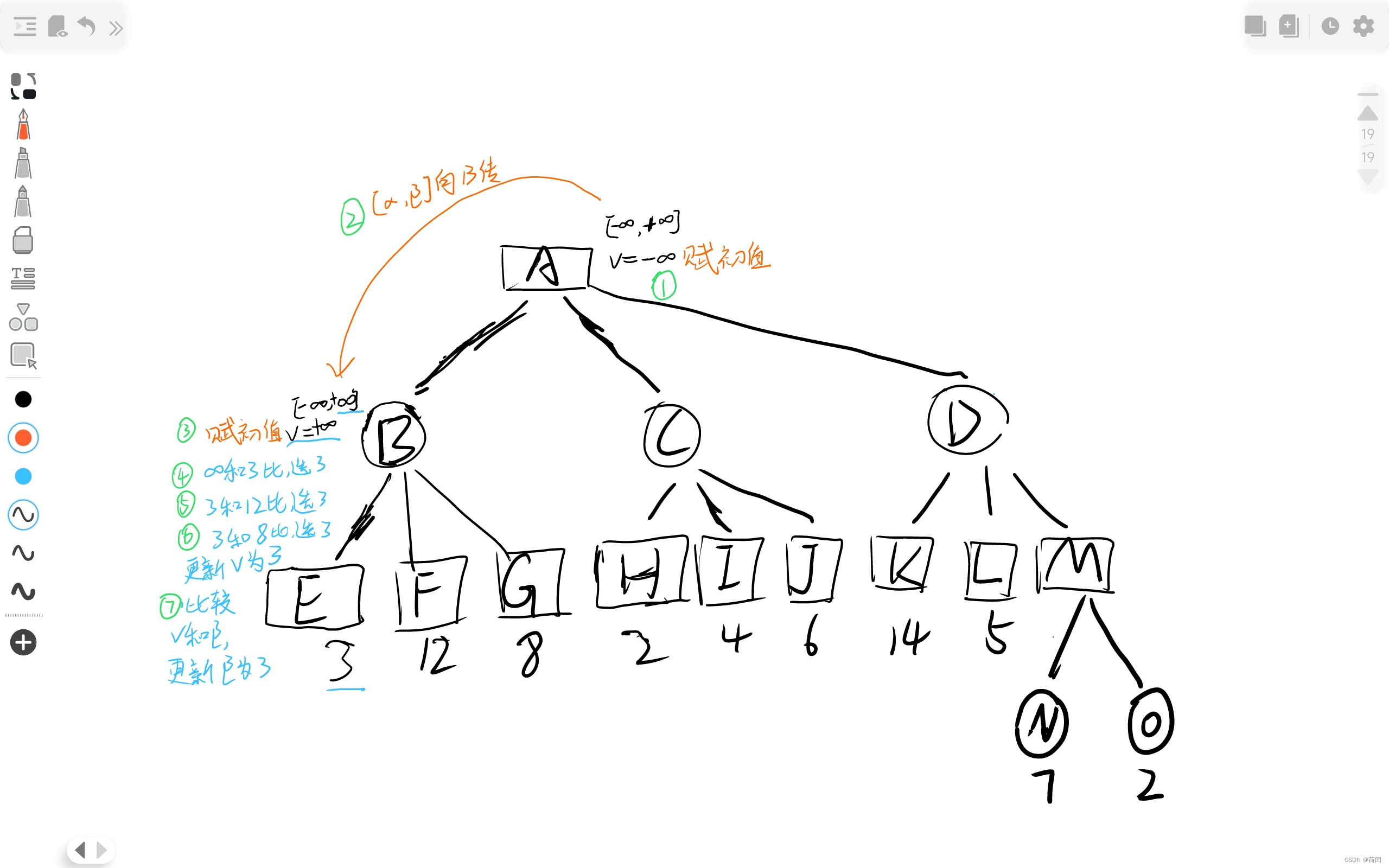
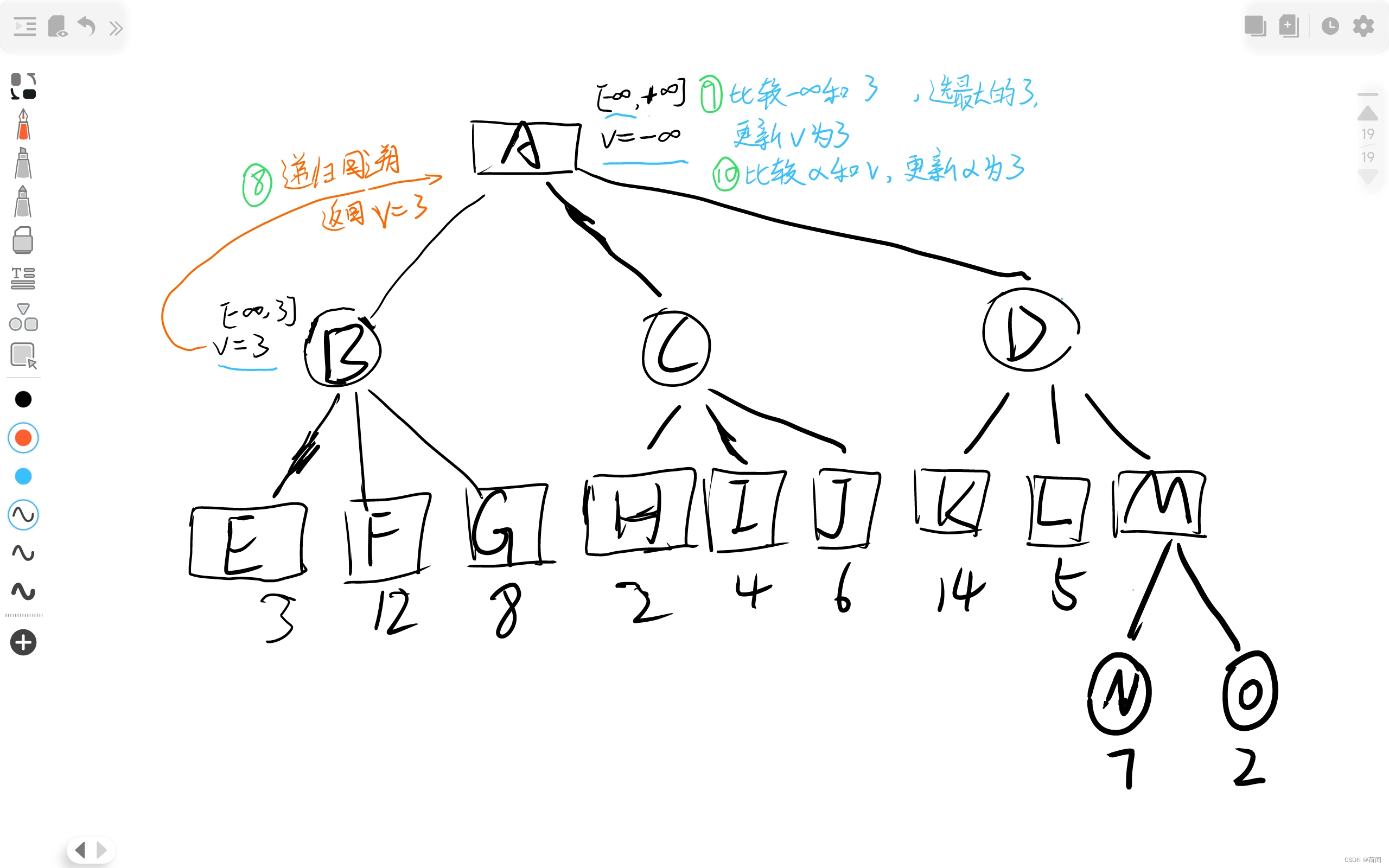
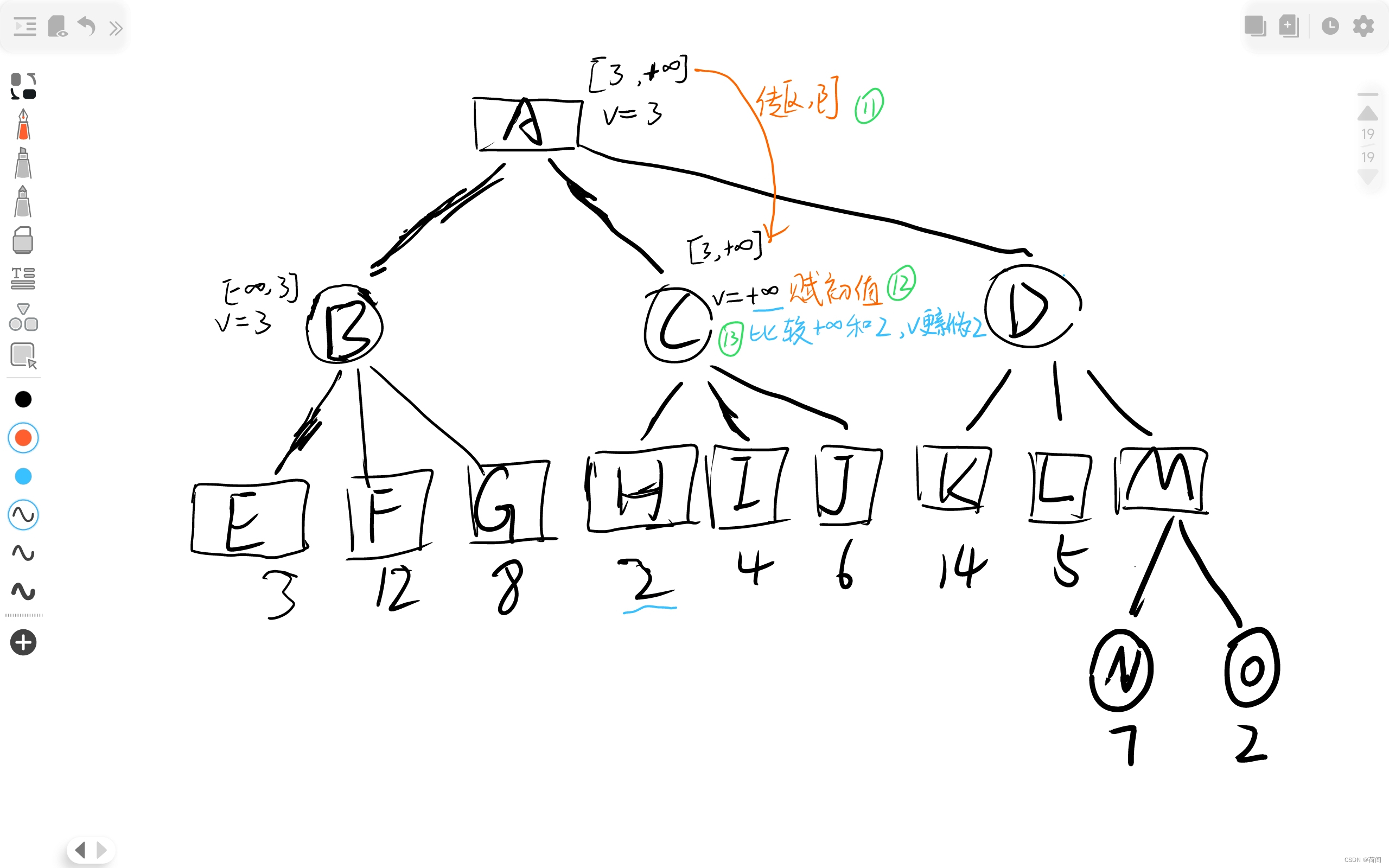
在这里插入图片描述

二、实验算法伪代码

读者可以对照下面的实验源码部分 ,下面的三个函数 (从上到下) 分别对应于源码中的 minmax_with_alphabeta
max_value
min_value

如果要真正搞懂, 请一定要去debug啊啊啊

在这里插入图片描述

三、实验算法代码

注意: 这个代码在python3.7.9下 (除了python3.10以上的 python3应该都可以) 可以直接运行, 输出的是路径

# -*- coding:utf-8 -*-import copy     # 注意对象的深拷贝和浅拷贝的使用！！！ #这个没有用到class GameNode:'''博弈树结点数据结构成员变量：name - string 结点名字val - int  结点值children - list[GameNode] 子结点列表'''def __init__(self, name='', val=0):self.name = name        # charself.val = val          # intself.children = []      # list of nodesclass GameTree:'''博弈树结点数据结构成员变量：root - GameNode 博弈树根结点成员函数：buildTree - 创建博弈树'''def __init__(self):self.root = None                # GameNode 博弈树根结点def buildTree(self, data_list, root):'''递归法创建博弈树参数：data_list - list[] like this ['A', ['B', ('E', 3), ('F', 12)], ['C', ('H', 2)], ['D', ('K', 14)]]root - GameNode'''# 请在这里补充代码，完成本关任务#********** Begin **********#if self.root == None:self.root = rootif type(data_list) == list:for listItem in data_list[1:]:root.children.append(GameNode(listItem[0]))else:  # 如果是元组,则进行节点赋值root.val = data_list[1]returnfor index in range(len(data_list[1:])):self.buildTree(data_list[1:][index], root.children[index])#********** End **********#class AlphaBeta:'''博弈树结点数据结构成员变量：game_tree - GameTree 博弈树成员函数：minmax_with_alphabeta - 带AlphaBeta剪枝的极大极小值算法，计算最优行动max_value - 计算最大值min_value - 计算最小值get_value - 返回结点的值isTerminal - 判断某结点是否为最终结点'''def __init__(self, game_tree):self.game_tree = game_tree      # GameTree 博弈树self.Alpha = -float('inf')self.Beta = float('inf')self.inf = float('inf')def minmax_with_alphabeta(self, node):'''带AlphaBeta剪枝的极大极小值算法，计算最优行动参数：node - GameNode 博弈树结点返回值：clf - GameNode 最优行动的结点'''# 请在这里补充代码，完成本关任务#********** Begin **********#res = self.max_value(node, self.Alpha, self.Beta)path = []path.append(node)# 利用节点树已经保存的节点信息,找到最佳决策路线# 其实这个 get_clfnode 函数有点问题,留给读者解决吧def get_clfnode(nodeTemp):for node in nodeTemp.children:if node.val == res and (node not in path):path.append(node)get_clfnode(node)get_clfnode(node)# 返回最好的决策路线return path#********** End **********#def max_value(self, node, alpha, beta):'''计算最大值参数：node - GameNode 博弈树结点alpha - int 剪枝区间下限值beta - int 剪枝区间上限值返回值：子结点中的最大的评估值'''# 请在这里补充代码，完成本关任务#********** Begin **********#if self.isTerminal(node):return node.valnode.val = -self.inffor child in node.children:node.val = max(node.val, self.min_value(child, alpha, beta))if node.val >= beta:return node.valalpha = max(alpha, node.val)return node.val#********** End **********#def min_value(self, node, alpha, beta):'''计算最小值参数：node - GameNode 博弈树结点alpha - int 剪枝区间下限值beta - int 剪枝区间上限值返回值：int 子结点中的最小的评估值'''# 请在这里补充代码，完成本关任务#********** Begin **********#if self.isTerminal(node):return node.valnode.val = self.inffor child in node.children:node.val = min(node.val, self.max_value(child, alpha, beta))if node.val <= alpha:return node.valbeta = min(beta, node.val)return node.val#********** End **********## def get_value(self, node):  # 没什么卵用,这函数#     '''返回结点的值#     参数：#     node - GameNode 博弈树结点#     返回值：#     clf - int 结点的值，即 node.val#     '''#     # 请在这里补充代码，完成本关任务#     #********** Begin **********##     return node.val#     #********** End **********#def isTerminal(self, node):'''判断某结点是否为最终结点（无子结点）参数：node - GameNode 博弈树结点返回值：clf - bool 是最终状态，返回True，否则返回False'''# 请在这里补充代码，完成本关任务#********** Begin **********#if len(node.children) != 0:return Falsereturn True#********** End **********## x = ['A', ['B', ('E', 3), ('F', 12)], ['C', ('H', 2)], ['D', ('K', 14)]]
x = ['A', ['B', ('E', 3), ('F', 12), ('G', 8)], ['C', ('H', 2), ('I', 4), ('J', 6)],['D', ('K', 14), ('L', 5), ['M', ('N', 7), ('O', 2)]]]# x = ['A', ['B', ('E', 3), ('F', 12), ('G', 8)], ['C', ('H', 2), ('I', 100), ('J', 100)], ['D', ('K', 14), ('L', 5), ('M', 2)]]
Tree = GameTree()
Tree.buildTree(x, GameNode(x[0]))AB = AlphaBeta(Tree)path = AB.minmax_with_alphabeta(AB.game_tree.root)print("最佳决策路线")
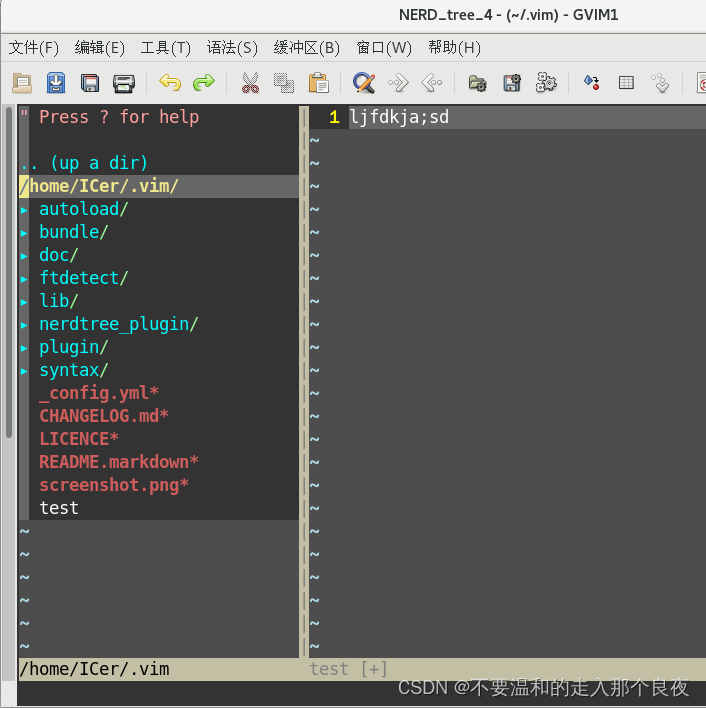
for node in path:print(node.name)