游戏规则
“一字棋"游戏（又叫"三子棋"或"井字棋”），是一款十分经典的益智小游戏。“井字棋"的棋盘很简单，是一个 3×3 的格子，很像中国文字中的"井"字，所以得名"井字棋”。"井字棋"游戏的规则与"五子棋"十分类似，"五子棋"的规则是一方首先五子连成一线就胜利；“井字棋"是一方首先三子连成一线就胜利。
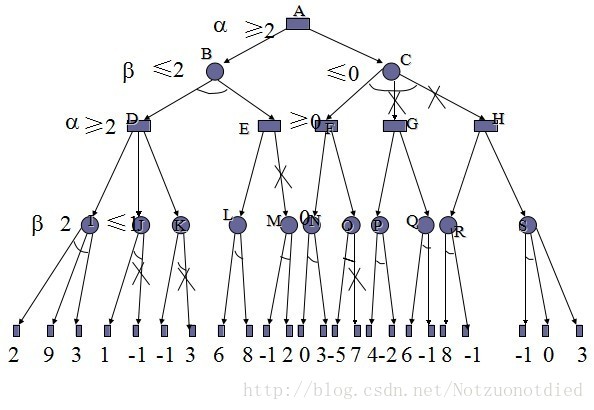
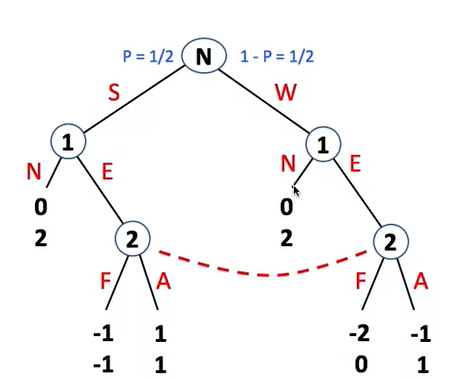
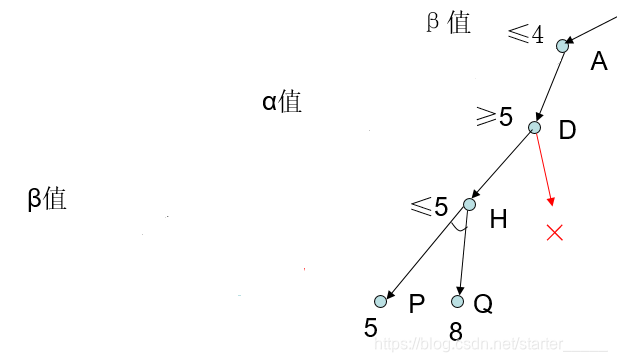
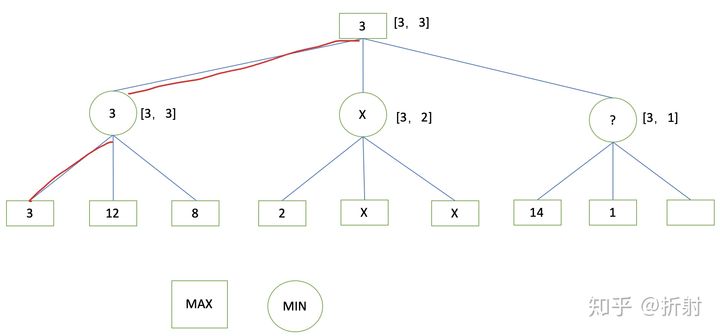
极小极大分析法
设有九个空格，由 MAX，MIN 二人对弈，轮到谁走棋谁就往空格上放一只自己的棋子，谁先使自己的棋子构成"三子成一线”(同一行或列或对角线全是某人的棋子)，谁就取得了胜利。
估价函数定义如下：设棋局为 P，估价函数为 e§。
(1) 若 P 对任何一方来说都不是获胜的位置，则 e§=e(那些仍为 MAX 空着的完全的行、列或对角线的总数)-e(那些仍为 MIN 空着的完全的行、列或对角线的总数)
(2) 若 P 是 MAX 必胜的棋局，则 e§＝+∞ （实际上赋了 60）。
(3) 若 P 是 B 必胜的棋局，则 e§＝-∞ （实际上赋了-20）。

# -*- coding: utf-8 -*-import random
import copy
import numpy as np
import matplotlib.pyplot as plt
from numpy.linalg import choleskyclass maps:def __init__(self,inf):#初始化self.matrix = [[" "]*3,[" "]*3,[" "]*3]for i in range(0,3):for j in range(0,3):self.matrix[i][j] = inf[i][j]self.cnt = 0 def __str__(self):return str( self.matrix[0] ) + "\n" +str( self.matrix[1] ) + "\n" +str( self.matrix[2] ) + "\n"def getvalue(self):for i in range(0,3):if self.matrix[0][i] == 'X' and self.matrix[1][i] == 'X' and self.matrix[2][i] == 'X' :return 100if self.matrix[0][i] == 'O' and self.matrix[1][i] == 'O' and self.matrix[2][i] == 'O' :return -100if self.matrix[i] == ['X', 'X', 'X']:return 100if self.matrix[i] == ['O', 'O', 'O']:return -100if self.matrix[0][0] == 'X' and self.matrix[1][1] == 'X' and self.matrix[2][2] == 'X' :return 100if self.matrix[0][0] == 'O' and self.matrix[1][1] == 'O' and self.matrix[2][2] == 'O' :return -100if self.matrix[0][2] == 'X' and self.matrix[1][1] == 'X' and self.matrix[2][0] == 'X' :return 100if self.matrix[0][2] == 'O' and self.matrix[1][1] == 'O' and self.matrix[2][0] == 'O' :return -100value = 0for i in range(0,3):if self.matrix[0][i] != 'O' and self.matrix[1][i] != 'O' and self.matrix[2][i] != 'O' :value += 1if self.matrix[0][i] != 'X' and self.matrix[1][i] != 'X' and self.matrix[2][i] != 'X' :value -= 1if self.matrix[0][i] != 'O' and self.matrix[1][i] != 'O' and self.matrix[2][i] != 'O' :value += 1if self.matrix[0][i] != 'X' and self.matrix[1][i] != 'X' and self.matrix[2][i] != 'X' :value -= 1if self.matrix[0][0] != 'O' and self.matrix[1][1] != 'O' and self.matrix[2][2] != 'O' :value += 1if self.matrix[0][0] != 'X' and self.matrix[1][1] != 'X' and self.matrix[2][2] != 'X' :value -= 1if self.matrix[0][2] != 'O' and self.matrix[1][1] != 'O' and self.matrix[2][0] != 'O' :value += 1if self.matrix[0][2] != 'X' and self.matrix[1][1] != 'X' and self.matrix[2][0] != 'X' :value -= 1return valuedef dfs(nowmaps , pre ,step):#博弈树核心算法#print(nowmaps,nowmaps.getvalue())if nowmaps.cnt == 9 or nowmaps.getvalue() == 100 or nowmaps.getvalue() == -100:return nowmaps.getvalue();if step % 2 ==0:value = 200for i in range(0,3):for j in range(0,3):if nowmaps.matrix[i][j] == ' ' :nowmaps.matrix[i][j] = 'O'nowmaps.cnt += 1 tmp = dfs(nowmaps,value,step+1)nowmaps.cnt -= 1 nowmaps.matrix[i][j] = ' 'if tmp < value:value = tmpif value <= pre :return valueelse:value = -200for i in range(0,3):for j in range(0,3):if nowmaps.matrix[i][j] == ' ' :nowmaps.matrix[i][j] = 'X'nowmaps.cnt += 1 tmp = dfs(nowmaps,value,step+1)nowmaps.cnt -= 1 nowmaps.matrix[i][j] = ' 'if tmp > value:value = tmpif value >= pre :return valuereturn valueif __name__ == '__main__':start = maps([[" "]*3,[" "]*3,[" "]*3])print(start)time = 0 while True :if start.getvalue() == 100 or start.getvalue() == -100:break print("轮到你下棋")x , y = input("输入下棋的点:").split()x = int(x)-1y = int(y)-1start.matrix[x][y]='O'start.cnt += 1 print("你下棋后")print(start)time += 1if time == 9:#下满了棋盘breakmaxvalue = -200for i in range(0,3):#遍历、寻找一个合适的点for j in range(0,3):if start.matrix[i][j] == ' ' :start.cnt += 1 start.matrix[i][j] = 'X'tmp = dfs(start,maxvalue,0)start.matrix[i][j] = ' 'start.cnt -= 1 if tmp > maxvalue:maxvalue = tmpx,y=i,jstart.matrix[x][y]='X'start.cnt += 1 print("电脑下棋后")print(start)time += 1#breakif start.getvalue() == -100 :print("胜利")elif start.getvalue() == 100 :print("失败")else:print("平局")