我在最近撰写五子棋AI程序设计报告时,翻阅了很多的资料博客,但却发现大佬们的博客,没有一篇是能让我只看它就能理解全部的AI算法。在看了众多博客后,我终于对博弈树、极大极小搜索、αβ剪枝恍然大悟,其实这些看似高大上的算法,其背后的想法都十分直白朴素。人们都说刚刚学会一项技能的人,是这个技能最好的老师,所以我便试着写了我这人生中的第一篇博客~
由于这是一篇算法原理博客,旨在让读者理解,里面就不包含代码了。以下关于算法原理的图片,是我从其他博客借鉴的,但是算法的举例分析完全是由刚刚理解的自己撰写,所以只要你一个字一个字地看,保证能明白!!!
废话少叙,上干货——
一、博弈树
(1)博弈的初始格局是初始节点
(2)在博弈树中,双方轮流扩展节点,假设有两方博弈,若A先走则成处于奇数深度的节点都应由A走,所有偶数级都应该由B走。
说白了博弈树就是对于棋盘状况的一种穷举!
以五子棋为例子:
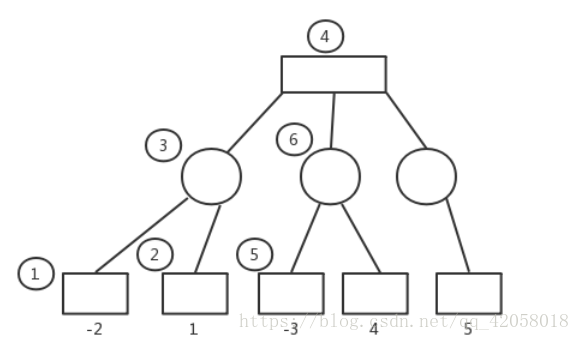
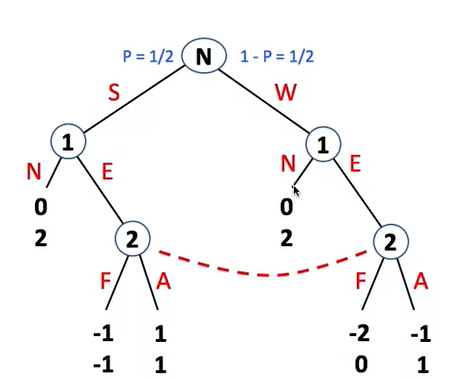
树中长方形结点为己方决策节点,圆圈结点为对方决策节点。每一个节点对应一种局面,有相应的评估函数算出来的分值(针对己方)。其中,每层的节点孩子的数目等于当前决策者所拥有的选择数量,所以博弈树每层节点的孩子数目逐层递减。(图中第一层三个孩子节点,由于我方已经进行决策,对方剩下的的选择数便只有两个,故第二层结点的孩子只有两个。)
二、极大极小搜索
在五子棋中,双方每一次落子,都会创造出一种新的局面。我们设计好计算局势得分的函数(针对A),来计算每一个局面对于A的得分,轮到A拓展结点(选择落子位置,即创造新局面)时,A会选择得分最大的,而B会选择得分最小的(A越糟糕B越开心)。
在决策树中,轮到我方决策层时,我们总希望做出得分最高的决策(得分以我方标准来算);而在敌方决策层时,我们假定敌方总能够做出得分最小的决策(我方得分最小便是相应敌方得分最高)。所以在博弈树中,每一层所要追求的结果,在极大分数和极小分数中不断交替,故称之为极大极小搜索。
注意啦!!!
由于一些同学提出我原先的MIN、MAX节点定义说的不太清楚,所以为了把知识掰碎了喂给大家,在此给出针对本文内容的确切定义,以下定义只在本文中生效:
1、方块节点:方块节点所在层称作MIN决策层,也就是敌方决策层,敌方会在所有方块节点中选择得分最小的一个
2、圆圈节点:圆圈节点所在层称作MAX决策层,也就是我方决策层,我方会在所有圆圈节点中选择得分最大的一个
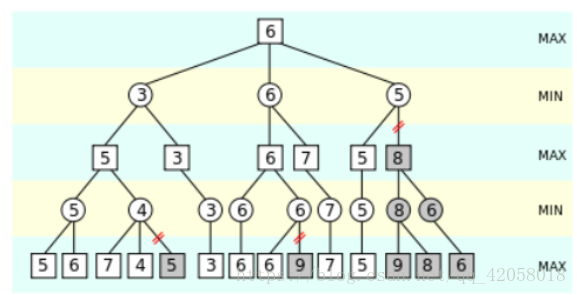
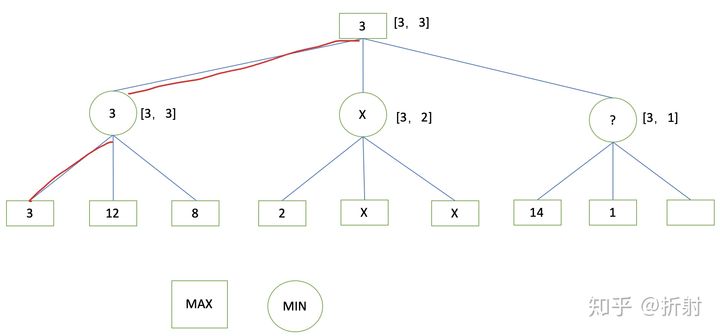
示例图片如下:
(请忽略上图中的MAX和MIN(反了),只看图感受就好,个人感觉我的定义更好理解)
我方要做出局势得分最大的决策,故称我方决策层为极大层;敌方要做出局势得分最小的决策,故称敌方决策层为极小层。
MINMAX的基本思想:f(p)指局势分数
- 当轮到敌方走步时,AI应该考虑最坏的情况(即f(p)取极小值)
- 当轮到我方走步时,AI应该考虑最好的情况(即f(p)取极大值)
- 相应于两位棋手的对抗策略,交替使用(1)和(2)两种方法传递倒推值
三、α,β剪枝
在极大极小搜索过程中,我们很明显地注意到,随着AI思考层数的上升,时间复杂度程指数级增长。当思考层数高时AI反应明显变慢,为了解决这个问题,我们采用α,β剪枝算法。
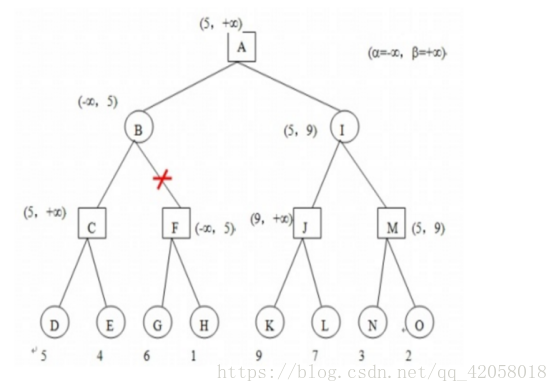
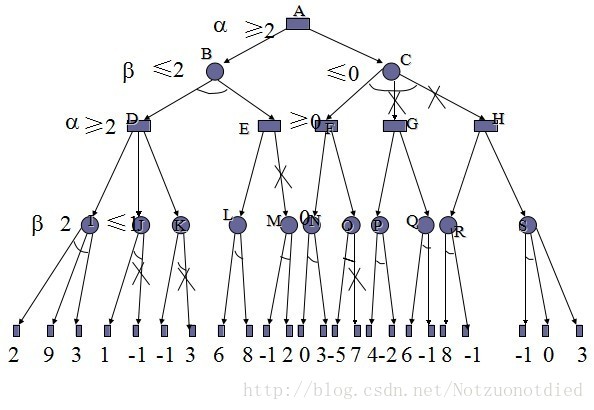
α,β剪枝算法是一种基于深度优先搜索的剪枝算法,示例如下图所示:
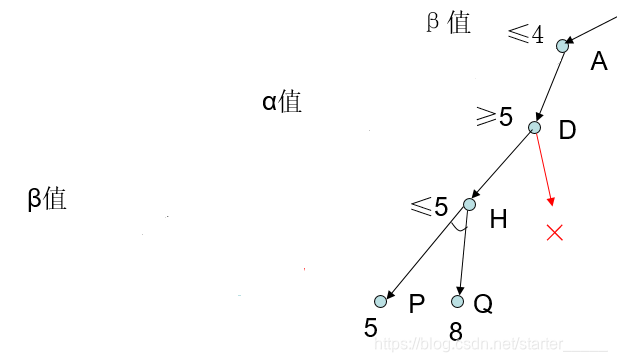
假设博弈树的搜索结果如图,正方形为MIN决策层,圆圈为MAX决策层。搜索结果D、E的评分分别为5和4,根据MAX决策准则,如果极小决策者选择C,那么对手势必会选择D,所以C方案所带给极小决策者的得分是5(记为α)。在搜索F方案的过程中,我们发现下一步极大决策者存在得分为6的方案G,所以F方案带给极小决策者的得分必然大于等于6,这个得分大于已经搜索完毕的方案C,所以对于极小决策者来说F方案已经不可能优于C方案,故不再需要计算F的其他子节点情况,剪去F分枝。
上述过程被称之为α剪枝,触发条件是MIN层方案的子结点出现大于α的得分,则剪去该条分枝。
β剪枝同理,触发条件时MAX层方案的子结点出现小于β的得分,则剪去该条分枝。
设游戏的时间复杂度为m^n,n为思考层数,理论上来说,经过排序的剪枝算法可以剪掉一半的n,使得思考层数可以翻倍。
欢迎关注笔者公众号~哥玛萌的小树洞