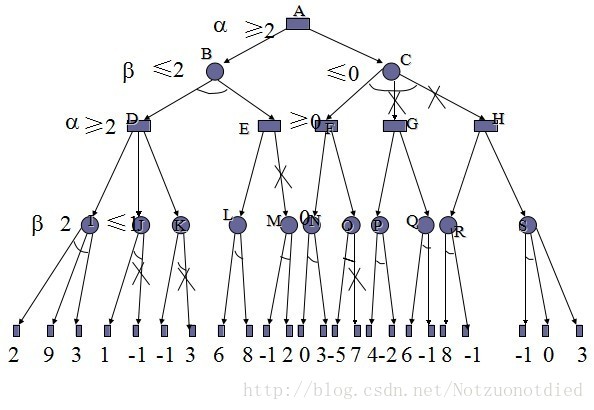
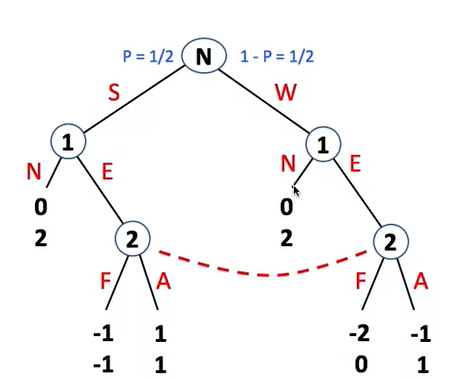
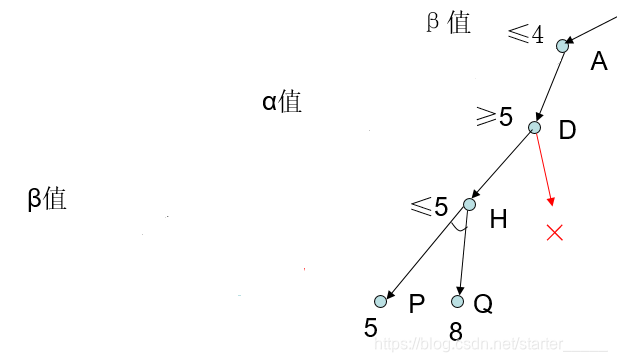
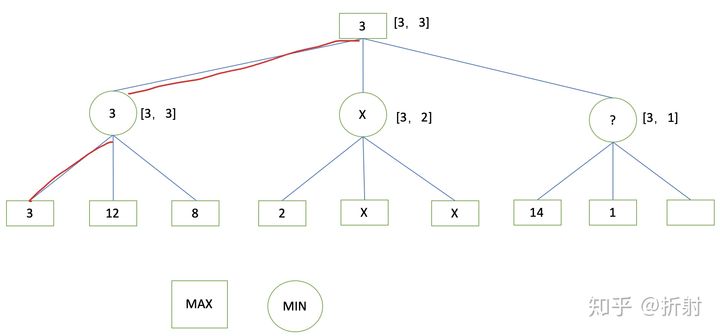
由于搜索的复杂度有点高，所以在树上减少计算量肯定是剪枝了，这里我们把剪枝的办法称作的：α-β剪枝

        我们在前面的文章中谈到，当第一次运作的是A，则所有的奇数深度的节点都是A做的选择，所有偶数深度的节点都是B做的选择。这很好理解，因为选手是轮流进行行为的。

        在前面的极大极小值的文章中也提到，我们选择A作为我们自己，我们当然要选择最优方案，即评估值为MAX，当然作为对手来说，他们要选择的当然是对我们评估值最小的为MIN。

MAX节点的评估下限值α：

　　作为MAX节点，假定它的MIN节点有N个，那么当它的第一个MIN节点的评估值为α时，则对于其它节点，如果有高于α的节点，就取那最高的节点值作为MAX节点的值；否则，该点的评估值为α。

      其实，最通俗来讲就是对于MAX节点，就是下一个深度中的最大值。

MIN节点的评估上限值β：

　　作为MIN节点，同样假定它的MAX节点有N个，那么当它的第一个MAX节点的评估值为β时，则对于其他节点，如果有低于β的节点，就取最低的节点值作为MIN节点的值；否则，该店的评估值为β。

      其实，最通俗来讲就是对于MIN节点，就是下一个深度中的最小值。

PS：这就是由子节点推父节点的值！

举例：>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>