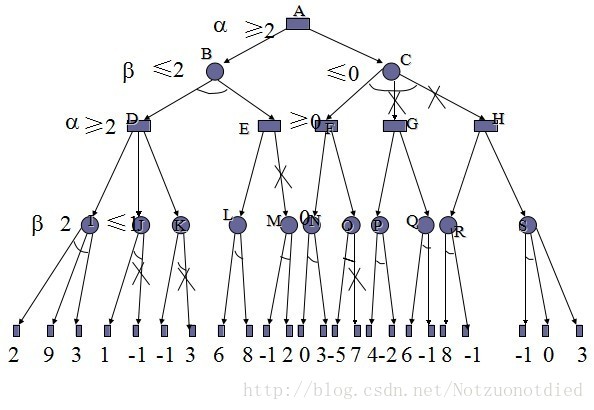
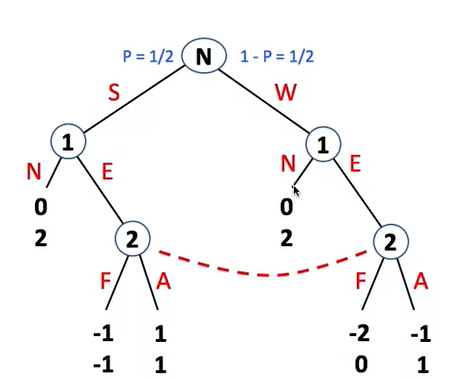
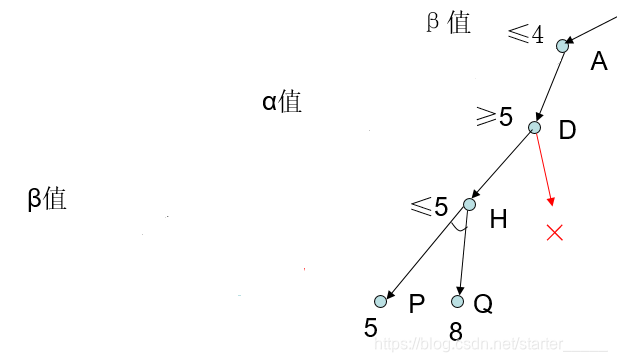
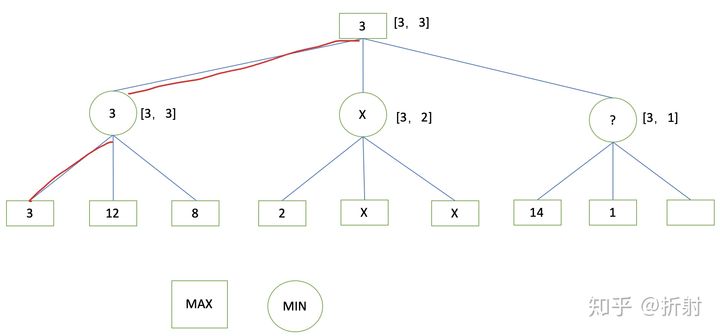
3.1 Alpha-Beta算法
虽然博弈树的状态是有限的,但是状态个数却非常多.假设博弈树的深度为d,每个结点有b个分支,即分支因子（branchingfactor）为b,那么使用Min-Max方法搜索这个博弈树需要搜索
个结点.
然而幸运的是,Min-Max方法的一些搜索是没有必要的,故此可以剪除（cut-off）那些没有必要搜索,即对搜索进行剪枝（prune）.Alpha-Beta算法是一种有效而常用的剪枝算法.
Alpha-Beta算法是在Min-Max方法基础上的一个改进.它维护一个搜索窗口（search window）:[α, β].其中α表示在搜索进行到当前状态,当前对抗者能确保达到的最大的结点值.在进一步的搜索中,将竭力提高α这个下限.而β表示在搜索进行到当前状态,在对手逼迫下,当前对抗者所达到的最大的博弈值.如果α > β,那么就没有必要再搜索这个结点及其子结点了.
实际上,可以证明,剪除的这一段搜索也不可能搜索到最小最大值.也可以证明[4],使用搜索窗口[α = -∞, β = +∞]对根位置（root position）进行搜索,Alpha-Beta算法可以返回最小最大值.
AlphaBeta(node, alpha, beta)
1: if node.depth = 0 then
2: return EvaluateNegaMax(node)
3: for i ← 1 to node.branch.length
4: new_node ← Traverse(node, node.branch[i])
5: value ← -AlphaBeta(new_node, -beta, -alpha)
6: if value ≥ beta then
7: return beta
8: if value > alpha then
9: alpha ← value
10: return alpha
3.2 Alpha-Beta算法的分析
3.2.1 Alpha-Beta算法的结点分类
按照[4]的方法,可以把博弈树中的结点进行分类,即对每个结点node,其种类node.type都有以下式子[5]:
其中type 1的结点又称为主变量结点（PrincipalVariation Nodes, 简称PV nodes）[1],因为主变量上的所有结点都是type 1,所有PV的结点又都在主变量上.由于搜索根结点是的搜索窗口为[-∞, +∞],所以PV结点的初始搜索窗口也为[-∞, +∞].假设PV结点搜索完成时,返回的子树博弈值为V,那么V是搜索其他子树的搜索窗口的下限.
type 2的结点又称为CUT结点.一个PV结点的第一个子结点也是PV结点,而它的其他子结点都是CUT结点.由于PV结点的第一个子结点总是比其他子结点先搜索完成,所以搜索CUT结点时,其父结点总是得到了第一个子结点的博弈值V.因此CUT结点的初始搜索窗口为[-∞, -V].由于博弈树是良序的,所以对CUT结点第一个子结点的搜索会立即引发一个剪枝,即CUT结点的子结点中除了第一个子结点都会被剪枝,所以这类结点是未定义的（undefined）.
type 3的结点又称为ALL结点.ALL结点的父结点必定是CUT结点,而且其祖先结点中必定至少有一个结点是PV结点.对于满足这个条件的最小祖先结点,如果该结点的第一个子结点的博弈值为V,那么该ALL结点的初始搜索窗口位[V, +∞],其父结点的初始搜索窗口为[-∞, -V].
3.2.2 良序的博弈树
如果一棵树博弈树的每个内部结点的第一个子结点都返回最优的解,那么称这棵树是良序的.对一个良序的博弈树,Alpha-Beta算法会修剪一些无必要搜索的子树,修剪之后的树就称为最小树（minimal tree,或者critical tree）.当博弈树是良序的时候,Alpha-Beta算法所需要搜索子树都包含在这个最小树中.按照上述结点的分类方法,最小树中的所有结点的类型都是已定的,因为那些类型为undefined的结点都会被剪枝.
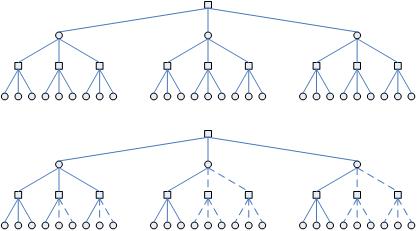
均匀博弈树及其最小树
如果一个博弈树的所有内部结点（interior node）具有相同的分支因子,且所有的根结点到叶结点的深度相同,那么该搜索树就是一个均匀的（uniform）.对于一个深度为d的均匀良序博弈树的的最小树,从根结点到叶结点,经历了d个边.设第i个边是其父结点的第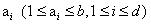
个分支.将所有
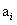按照“.”连接起来形成一个串:
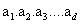.设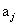
为该串中第一个大于1的值.如果不存在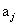,即所有的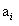
都为1,则该叶结点为PV结点.如果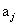存在,那么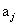对应边的子结点一定为CUT结点.这时如果d - j是偶数,那么该串对应的叶结点为CUT结点,否则,如果d - j是奇数,该叶结点为ALL结点.
对一个CUT类型的叶结点,它对应的串存在着性质:对所有i,如果d - j是偶数,则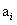为1.这种串（除了全1的串）和CUT叶结点一一对应.这种串的个数为
,故此CUT叶结点的个数也为.
同样,对一个ALL类型的叶结点,它对应的串存在着性质:对所有i,如果d - j是奇数,那么为1.这样的串（除了全1的串）和ALL叶结点一一对应.这样的串的个数为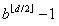
,所以ALL叶结点的个数为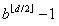.再加上PV叶结点,一个最小树包含的叶结点个数为
,这也是在均匀博弈树中Alpha-Beta算法搜需要搜索的最少叶结点个数.
3.2.3 强有序的博弈树
很多时候,并不能做到让博弈树完全良序,但是可以通过存储表,启发式等方法改进Alpha-Beta算法,使得博弈树呈现较好的有序性.均匀博弈树的强有序性定义为[6]:
a. 以很高的概率（例如,70%）,每个结点的第一个分支是最优的.
b. 以很高的概率（例如,90%）,最优的决策位于搜索的前一少部分（例如,搜索的前1/4）.
相对的,均匀博弈树的随机性定义为该搜索树的叶结点的值在固定区间内随机分布.
如果定义R(b, d)为在随机的归一化博弈树中需要搜索的叶结点的平均个数.定义S(b, d)为在强有序的归一化博弈树中需要搜索的叶结点的平均个数.那么有以下不等式:
= B(b, d) < S(b, d)< R(b, d) << M(b, d) =
本文章欢迎转载，请保留原始博客链接http://blog.csdn.net/fsdev/article
-------------------
[1] Valavan Manohararajah(2001). Parallel Alpha-Beta Search on SharedMemory Multiprocessors. Master’s thesis, Graduate Department of Electrical andComputer Engineering, University of Toronto, Canada.
[2] A. Newell and H.A. Simon (1972). Human Problem Solving.Prentice-Hall, 1972.
[3] Stuart Russell and Prter Norvig (1995). Artificial Intelligence, AModern Approach. Prentice-Hall, Egnlewood Cliffs, 1995.
[4] Knuth, D.E. and Moore, R.W. (1975). An Analysis of Alpha-Beta Pruning.Artificial Intelligence, 6:293–326.
[5] Hopp, Holger and Sanders, Peter (1995). Parallel Game Tree Search onSIMD Machines. IRREGULAR '95: Proceedings of the Second International Workshopon Parallel Algorithms for Irregularly Structured Problems. 349-361.
[6] Marsland, T.A. and Campbell, M.S. (1982). Parallel Search ofStrongly Ordered Game Trees. ACM Computing Surveys, Vol. 14, No. 4, pp.533-551. ISSN 0360-0300.
