一、概述

博弈的概念

博弈是一类具有智能行为的竞争活动，如下棋、战争等。

博弈的类型

• 双人完备信息博弈：两位选手（例如MAX和MIN ）对垒，轮流走步，每一方不仅知道对方已经走过的棋步，而且还能估计出对方未来的走步。
• 机遇性博弈：存在不可预测性的博弈，例如掷币等。

博弈树

若把双人完备信息博弈过程用图表示出来，就得到一棵与/或树，这种与/或树被称为博弈树。在博弈树中，那些下一步该MAX走步的结点称为MAX结点，下一步该MIN走步的结点称为MIN 结点。

博弈树的特点

1. 博弈的初始状态是初始结点；
2. 博弈树中的“或”结点和“与”结点是逐层交替出现的；
3. 整个博弈过程始终站在某一方的立场上，例如MAX方。所有能使自己一方获胜的终局都是本原问题，相应的结点是可解结点；所有使对方获胜的终局都是不可解结点。

---

二、极大极小过程

（1）算法思想

极大极小过程用当前正在考察的结点生成一棵部分博弈树，并利用估价函数f(n)对叶结点进行静态估值。

求叶结点的值

• 对MAX有利的结点，其估价函数取正值
• 对MIN有利的结点，其估价函数取负值
• 使双方均等的结点，其估价函数取接近于0的值。

求非叶结点的值：

必须从叶结点开始向上倒退。其倒退方法是：

• 对于MAX结点，由于MAX 方总是选择估值最大的走步，因此，MAX结点的倒退值应该取其后继结点估值的最大值。
• 对于MIN结点，由于MIN方总是选择使估值最小的走步，因此MIN结点的倒推值应取其后继结点估值的最小值。
• 这样一步一步的计算倒推值，直至求出初始结点的倒推值为止。这一过程称为极大极小过程。

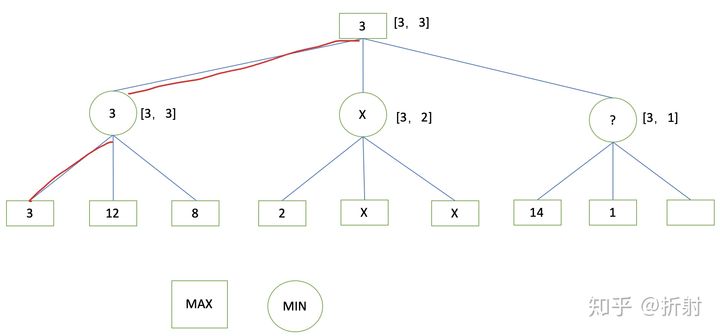
（2）极大极小过程实例

---

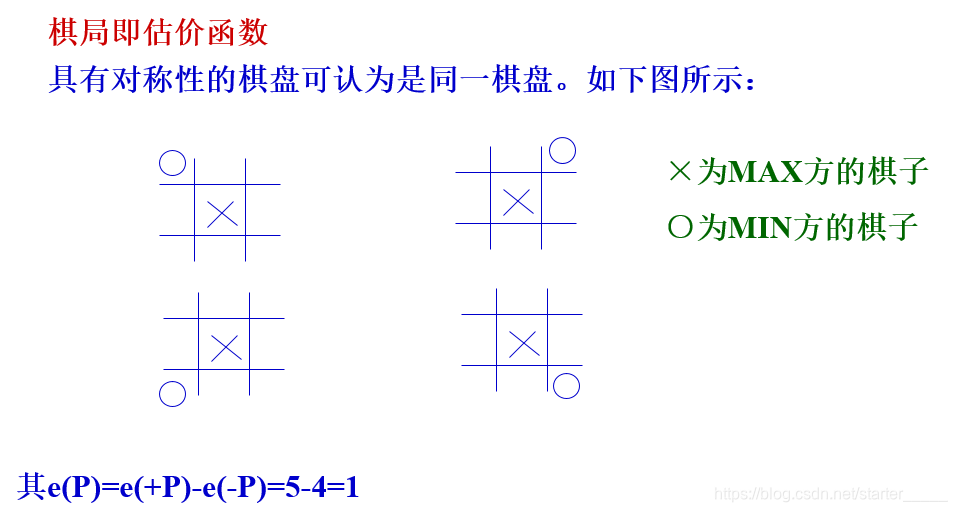
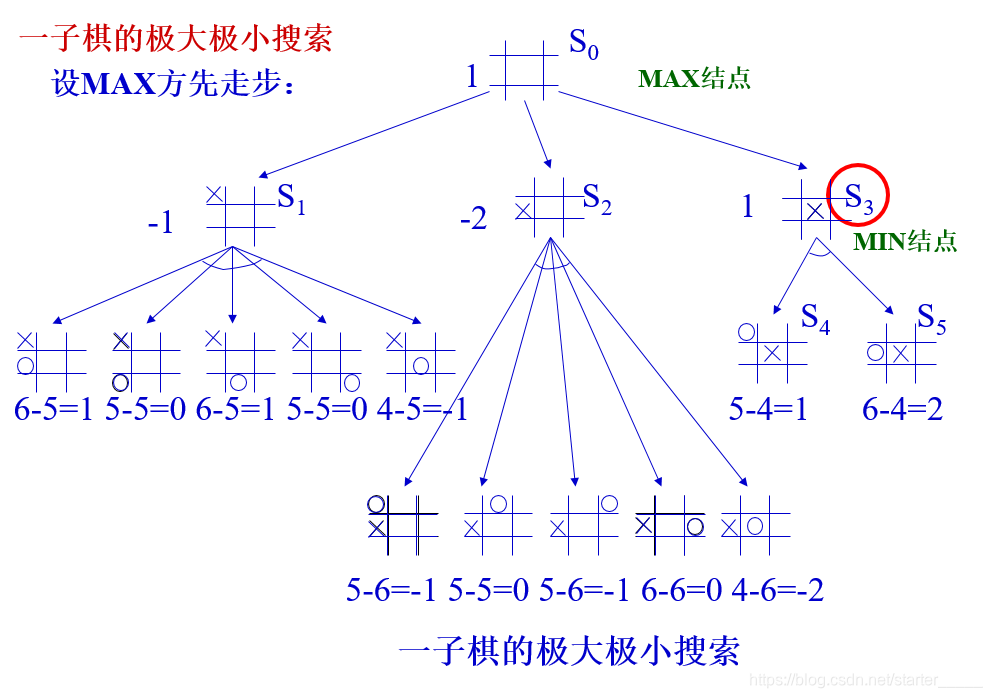
三、α-β剪枝

（1）算法思想

极大极小过程是先生成与/或树，然后再计算各结点的估值，这种生成结点和计算估值相分离的方式，需生成规定深度内的所有结点，搜索效率较低。如果能边生成结点边对结点估值，并剪去一些没用的分枝，这种技术被称为α-β剪枝。

剪枝方法

1. MAX结点（或结点）的α值为当前子结点的最大倒推值；
2. MIN结点（与结点）的β值为当前子结点的最小倒推值；
3. α-β剪枝的规则如下：

• β剪枝： 任何MAX结点n的α值大于或等于它先辈结点的β值，则n 以下的分枝可停止搜索，并令结点n的倒推值为α。这种剪枝称为β剪枝。
• α剪枝： 任何MIN结点n的β值小于或等于它先辈结点的α值，则n 以下的分枝可停止搜索，并令结点n的倒推值为β。这种剪枝称为α剪枝。

（2）α-β剪枝实例

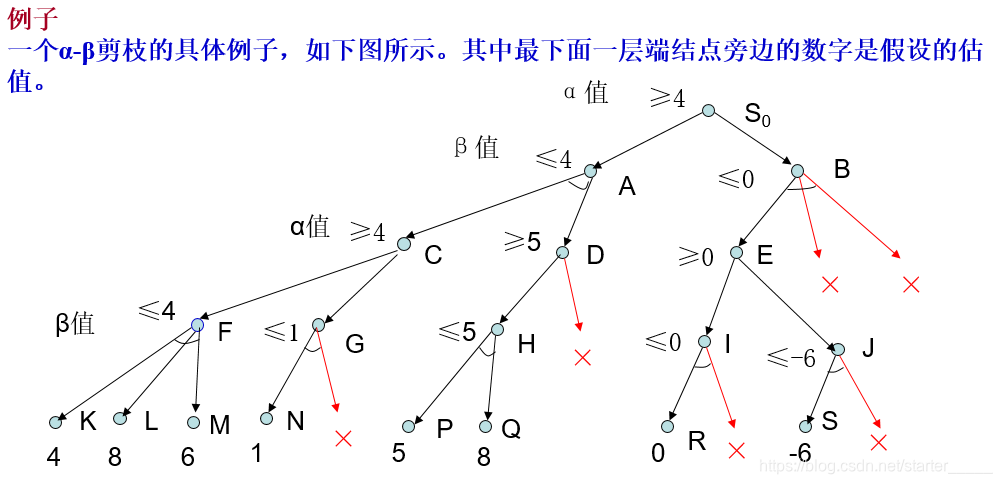
1. 剪枝1：

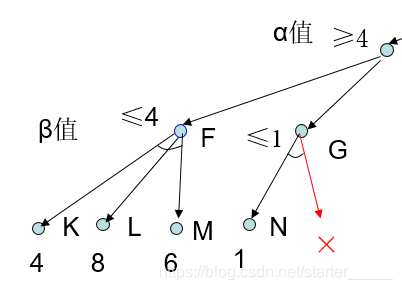
α剪枝： MIN结点G的β值(<=1)小于或等于它先辈结点C的α值(>=4)，结点G不可能让先辈结点C的α值增大，则G以下的分枝可停止搜索，并令结点n的倒推值为β(<=1)。这种剪枝称为α剪枝。

详解： 在该图中，K、L、M的估值推出结点F的到推值为4，即F的β值为4，由此可推出结点C的到推值≥4。 记C的到推值的下界为4，不可能再比4小，故C的α值为4。由结点N的估值推知结点G的倒推值小于≤1,无论G的其它子结点的估只是多少，G的倒推值都不可能比1大。因此，1是G的倒推值的上界，所以G的值≦1 。另已知C的倒推值≥4，G的其它子结点又不可能使C的倒推值增大。因此对G的其它分支不必再搜索，相当于把这些分枝剪去。

2. 剪枝2：

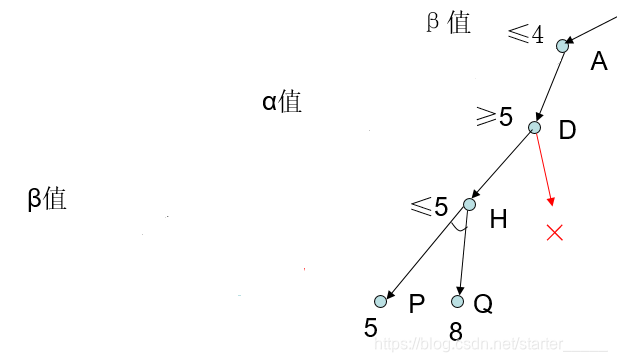
β剪枝： MAX结点D的α值（>=5）大于它先辈结点A的β值（<=4），则D以下的分枝可停止搜索，结点D不可能让先辈结点A的β值减小，并令结点D的倒推值为α（>=5）。这种剪枝称为β剪枝。

详解： 由F、G的倒推值可推出结点C的倒推值≥4 ，再由C可推出结点A的倒推值≤4，即A的β值为4。另外，由结点P、Q推出的结点I的倒推值为5，因此D的倒推值 ≥5，即D的α值为5。此时，D的其它子结点的倒推值无论是多少都不能使D及A的倒推值减少或增大，所以D的其他分枝被减去，并可确定A的倒推值为4 。

3. 其它剪枝（省略）